2021学年1 平行四边形的性质备课课件ppt

这是一份2021学年1 平行四边形的性质备课课件ppt，共22页。PPT课件主要包含了活动1，图形无处不在，活动2，活动3合作探究，平行四边形的性质，角对角相等，边对边平行且相等，活动4知识应用，例题教学，数学思想等内容，欢迎下载使用。
大家知道什么样的四边形叫平行四形吗？
自主学习：阅读课本135-136页
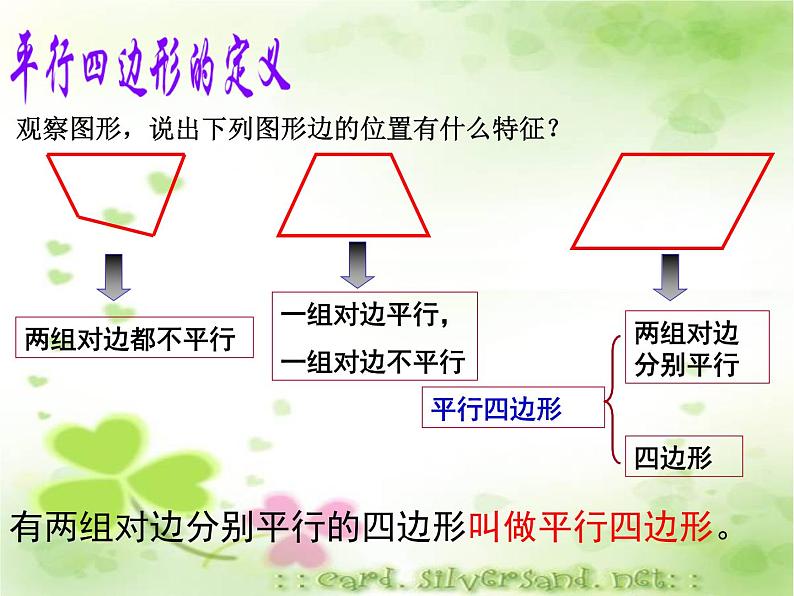
一组对边平行，一组对边不平行
有两组对边分别平行的四边形叫做平行四边形。
观察图形，说出下列图形边的位置有什么特征？
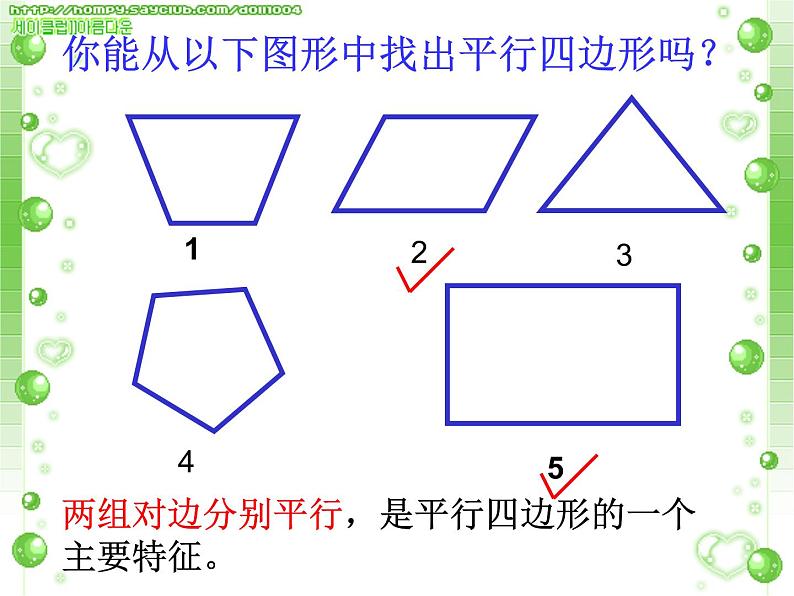
你能从以下图形中找出平行四边形吗？
两组对边分别平行，是平行四边形的一个主要特征。
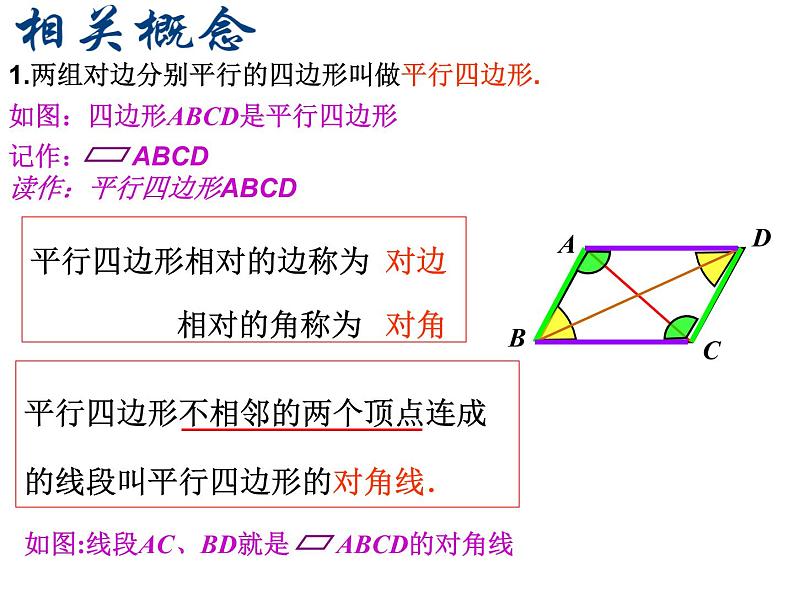
平行四边形相对的边称为 对边 相对的角称为 对角
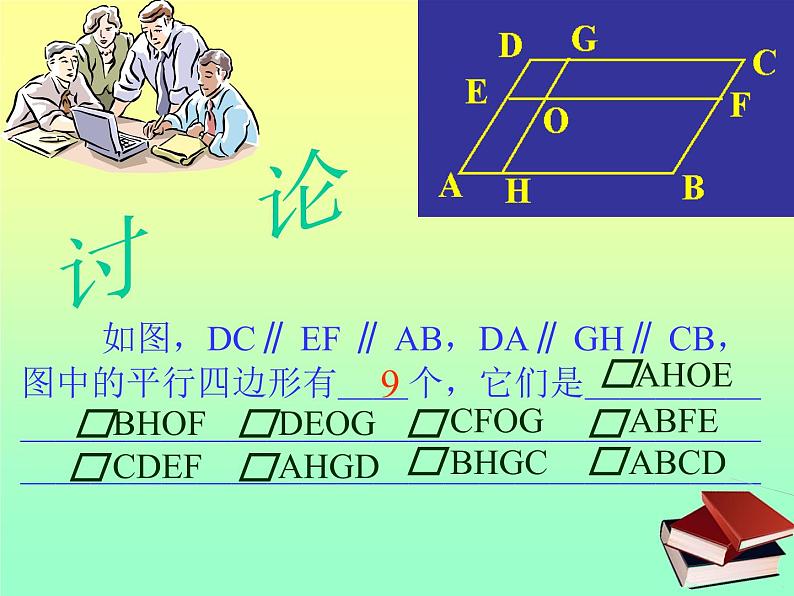
如图，DC∥ EF ∥ AB，DA∥ GH∥ CB，图中的平行四边形有＿＿个，它们是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
复制一个平行四边形使它与原平行四边形重合，再用大头针把对角线的交点Ｏ固定，把上面平行四边形绕点Ｏ旋转180°，它与原来的四边形ABCD重合吗？ 通过旋转探究边，角的关系？
□ABCD是中心对称图形,对称中心是对角线的交点O
绕它的中心O旋转180°后与自身重合
平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C，∠B=∠D.
平行四边形的对边相等.
∵四边形ABCD是平行四边形∴AB=CD，BC=AD.
平行四边形的对边相等，对角相等。
已知：四边形ABCD是平行四边形。求证：AD=BC,AB=CD ∠A= ∠C, ∠B= ∠D.
提示：可连接AC，试证⊿______≌ ⊿______
在解决平行四边形的问题时，通常可以连结对角线转化为两个全等的三角形进行解题。
已知： ABCD 求证（1）AB=CD BC=DA；
∵四边形ABCD是平行四边形∴AB∥CD，AD∥BC
∴∠1＝∠2，∠3＝∠4
∠1＝∠2AC＝CA∠3＝∠4
∴ △ABC≌△CDA（ASA）
∴AB＝CD，BC＝DA，
又∵∠1＝∠2，∠3＝∠4
∴∠1＋∠4＝∠2＋∠3
在△ABC和△CDA中
（2）∠B=∠D，∠A=∠C.
对称性：中心对称图形。
变式2：若平行四边形周长为54cm，两邻边之差为5cm，则这两边的长度分别为: .
知识点：平行四边形对边相等
知识点：平行四边形对角相等，邻角互补。
例2、已知：如图在平行四边形ABCD中，E、F分别是BC和AD上的点，且BE=DF.求证：AE=CF.
证明:∵四边形ABCD是平行四边形 ∴AB = CD ∠B=∠D
在△ABC和△CDF中
AB＝CD∠B=∠D BE=DF
∴ △ABE≌△CDF（SAS）
变式训练： 如图，在平行四边形ABCD中，BE,DF分别是∠ABC和∠ADC角平分线。求证BF=DE.
平行四边形的对边平行且相等；
平行四边形的对角相等；邻角互补。
平行四边形是中心对称图形。
有两组对边分别平行的四边形是平行四边形。
课后作业必做题：课本137页习题6.1 --1、2、3选做题：平面直角坐标系中，已知三点A（－1，0），B（2，0），C（0，1），是否存在点D, 以A、B、C、D为顶点的四边形是平行四边形，．若存在，求出D点坐标；若不存在，请说明理由．
1.在ABCD中，∠A︰∠B︰∠C︰∠D的值可以是（ ） A、1︰2︰3︰4 B、3︰4︰4︰3 C、3︰3︰4︰4 D、3︰4︰3︰42.在平行四边形ABCD中，若AE平分∠DAB，AB=5cm,AD＝9cm,则EC＝ .
学校买了四棵树，准备栽在花园里，已经栽了三棵（如图），现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树栽在的方案有几种？