



衢州、丽水、湖州2022年4月三地市高三教学质检数学试卷及解析
展开衢州、丽水、湖州三地市教学质量检测试卷
参考解析(2022.04)
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
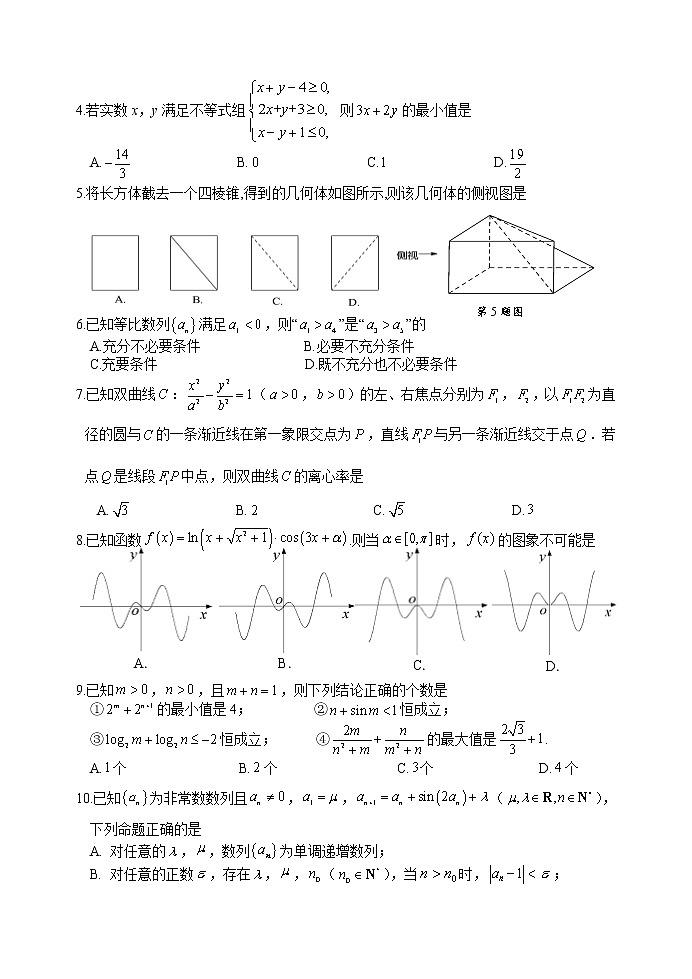
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | B | D | C | C | A | B | D | C | B |
9.【解析】:①选项:,“=”取到时,解得,与题设矛盾,故,无最小值.
②选项:恒成立,故B正确.
③选项:,,那么,C正确.
④选项:,令,则
则原式=,(“=”取到时)D正确.
综上故选C.
10.【解析】:对于选项A:若数列为单调递增数列,则恒成立,得,所以A错误.
对于选项B:本选项是考查数列的极限,由不动点知识,对中令得,当带入不动点方程时,又可得或者所以取,,所以由蛛网图可知B正确.
对于选项C:要使得是周期的周期数列,有递推关系图像可知,在该图像上应存在不同的两点关于对称,则递推函数图像与图像应有两不同的交点,且两交点关于对称。令函数,而,所以是上的单调递增函数,不可能有两不同的零点,即方程不可能有两不同的根,也所以C错误.
对于选项D:由递推可得,所以D错误.
二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)
11. 12. , 13. , 14. ,
15. , 16. 17.
16.【解析】:由,可得的轨迹为椭圆,以为轴建系,则的轨迹方程为.
其中,由题可得只需的最小,将关于对称可得,故转化为求的最小,显然最小值为.
17.【解析】:设,则,
则,解得,
又因为当,.
此时问题转化为:恒成立,则须,解得.
三、解答题(本大题共5小题,18题14分,其余各题15分,共74分)
18.已知函数,.
(I)求函数的单调递增区间;
(II)求函数的值域.
解:(Ⅰ).----------------------------------------3分
则.-------------------------------------------------------------------5分
得,
所以函数的单调递增区间是().-------------------7分
(Ⅱ).--------------------------------------9分
.---------------------------------------------------------------12分
所以函数的值域为.----------------------------------------------------14分
19.如图,已知三棱台中,二面角的大小为,点在平面内的射影在上,,,.
(I)证明:平面;
(II)求直线与平面所成角的正弦值.
解:(Ⅰ)由可知,
又因为与平行,所以.……………………3分
因为平面,所以,
又因为,所以平面.………………………………6分
(Ⅱ)方法一:过作垂直于交于,连,因为平面,所以即为二面角的平面角,所以.…………………9分
在中,,,可得.
在中,,.
在中,,,
在中,因为,所以.
又因为,由余弦定理可得,
所以.………………………………………………11分
设点到平面的距离为,直线与平面所成角为,
由可得,
所以.………………………………………………13分
所以.………………………………………………15分
方法二:如图建立空间直角坐标系,则,,
因为,,二面角的大小为,
所以,.……………………9分
设平面的法向量为,则
可得,
取可得.………………………………………………12分
直线与平面所成角为,
则.…………………………………15分
20.已知等差数列的前项和为,满足,.数列满足,
,.
(I)求数列,的通项公式;
(II)设数列满足,,记数列的前项和为,若,
求的最小值.
解:(I)由题可得:,
解得,所以.------------------------------------------------------2分
因此.----------------------------------------------------------------------4分
.---------------------------------------------------------------6分
.------------------------8分
(II)由(I)可得:
.------------------------------------------------------9分
所以.-----------------------12分
即,
又因为,单调递减,且,
所以解得:,故的最小值为.…………15分
21.如图,拋物线()上的点()到其准线的距离为2.过点作直线交拋物线于,两点,直线与直线交于点.
(I)求证:直线轴;
(II)记,的面积分别为,.
若,求直线的方程.
解:(Ⅰ)由条件可知,得.--------2分
故,即.--------------------------------3分
且故抛物线方程为,
设直线的方程为,
则由,得.------------------------4分
有,所以且.-----------------5分
由,解得.-----------------------------------------6分
又共线,所以,
又,,
则,
化简可得,
解得或(舍去),所以.
因此轴.---------------------------------------------------------------------------------8分
(Ⅱ)由题意可知轴,所以
因此.---------------------------------------------------------------------9分
.-----------------------------------------------11分
.------------------------------------------------------------------------------12分
所以.--------------------------------------------------------13分
解得或
因此所求的方程为或.-----------------------------------------15分
【另解】(Ⅰ)由条件可知,得.------------------2分
故,即.-----------------------------------------3分
故抛物线方程为,
设(),则直线方程为.----------------4分
由,解得.------------------6分
又共线,所以,又,,则,
解得,
所以.
因此轴.---------------------------------------------------------------------------8分
(Ⅱ)由题意可知轴,所以
因此.-------------------------------------------------------------------9分
.-------------------------------------------11分
.------------------------------------------------------------------12分
所以.----------------------------------------------13分
解得或
因此所求的方程为或.--------------------------------------15分
22.已知函数.
(Ⅰ)若,求函数的极小值点.
(Ⅱ)当时,讨论函数的图象与函数的图象公共点的个数,并证明你的结论.
解:(Ⅰ)若,函数,
.………………………………………………2分
由可得.…………………………………………………………4分
当时,,函数单调递减;
当时,,函数单调递增;
所以函数的极小值点是.……………………………………6分
(Ⅱ)由可得,.
记(),
则讨论函数的图象与函数的图象公共点的个数转化为讨论函数零点的个数.
,.……………………8分
(1)当即时,
函数在上单调递减,在上单调递增,.
①若即,则函数在没有零点.
②若即,则函数在恰有一个零点.
③若即,
因为,则函数在上有一个零点,
因为,
若即,则函数在上没有零点.
若即,则函数在上有一个零点.
所以当或时,函数在只有一个零点;
当时,函数在有两个零点;
当时,函数在没有零点.……………………11分
(2)当即时,函数在上单调递增,在上单调递减,在上单调递增.则极小值,所以函数在上没有零点.
因为,
因为,所以,所以,则函数在上有且只有一个零点.
所以当时函数在只有一个零点.……………………13分
综上可知,当时,函数的图象与函数的图象公共点的个数情况如下:
当时,没有交点;
当或或时,只有一交点;
当时,有两个交点.……………………15分
衢州、丽水、湖州 2023 年 11 月三地市高三教学质量检测数学试卷及参考答案: 这是一份衢州、丽水、湖州 2023 年 11 月三地市高三教学质量检测数学试卷及参考答案,文件包含衢州丽水湖州2023年11月三地市高三教学质量检测数学参考答案pdf、衢州丽水湖州2023年11月三地市高三教学质量检测数学试卷pdf等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
衢州、丽水、湖州 2023 年 11 月三地市高三教学质量检测数学试卷及参考答案: 这是一份衢州、丽水、湖州 2023 年 11 月三地市高三教学质量检测数学试卷及参考答案,文件包含衢州丽水湖州2023年11月三地市高三教学质量检测数学参考答案pdf、衢州丽水湖州2023年11月三地市高三教学质量检测数学试卷pdf等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
2024届11月衢州丽水湖州三地市高三教学质量检测-数学: 这是一份2024届11月衢州丽水湖州三地市高三教学质量检测-数学,文件包含2024届11月衢州丽水湖州三地市高三教学质量检测-数学答案pdf、2024届11月衢州丽水湖州三地市高三教学质量检测-数学试卷pdf等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。












