专题06锐角三角函数与解三角形-2022年中考数学二轮热点题型归纳与变式演练试卷（学生版+教师版）

这是一份专题06锐角三角函数与解三角形-2022年中考数学二轮热点题型归纳与变式演练试卷（学生版+教师版），文件包含专题06锐角三角函数与解三角形教师版docx、专题06锐角三角函数与解三角形学生版docx等2份试卷配套教学资源，其中试卷共75页， 欢迎下载使用。
一、热点题型归纳
【题型一】 锐角三角函数的概念与计算问题
【题型二】 利用锐角三角函数解决与三角形有关的问题
【题型三】 解直角三角形
二、最新模考题组练2
【题型一】 锐角三角函数的概念与计算问题
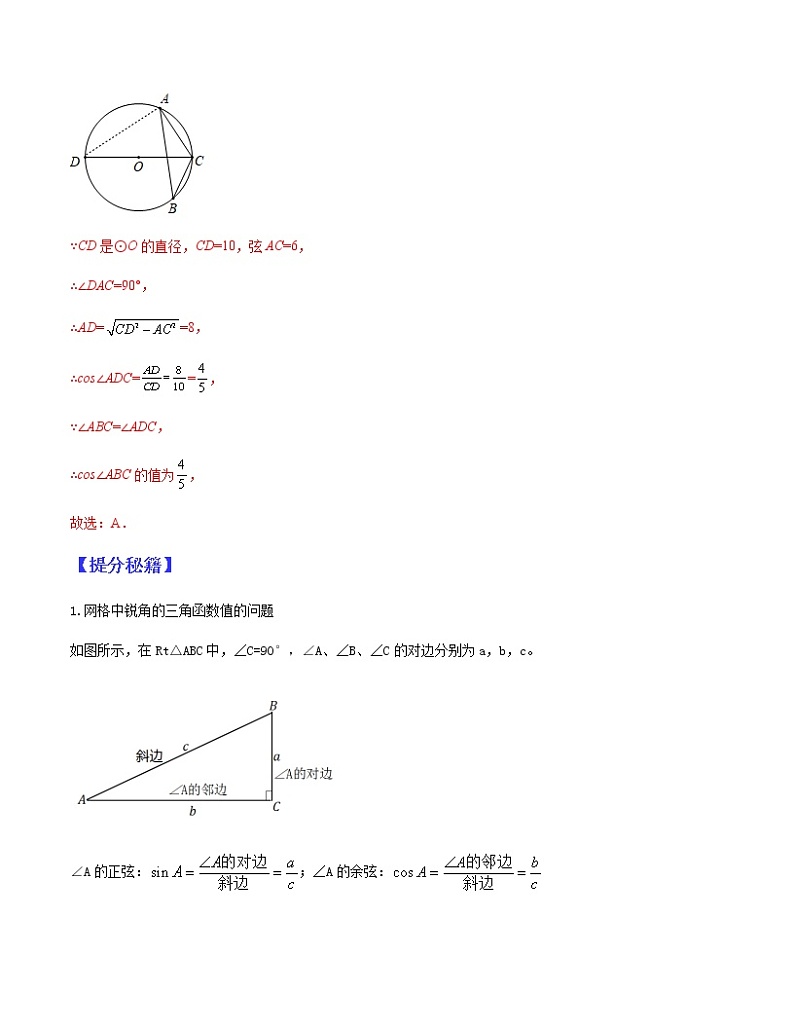
【典例分析】（2021·山东滨州·中考真题）如图，⊙O是△ABC的外接圆，CD是⊙O的直径．若，弦，则的值为（ ）
A．B．C．D．
【答案】A
【分析】连接AD，根据直径所对的圆周角等于90°和勾股定理，可以求得AD的长，然后即可求得∠ADC的余弦值，再根据同弧所对的圆周角相等，可以得到∠ABC=∠ADC，从而可以得到cs∠ABC的值．
【解析】解：连接AD，如右图所示，
∵CD是⊙O的直径，CD=10，弦AC=6，
∴∠DAC=90°，
∴AD==8，
∴cs∠ADC==，
∵∠ABC=∠ADC，
∴cs∠ABC的值为，
故选：A．
【提分秘籍】
1.网格中锐角的三角函数值的问题
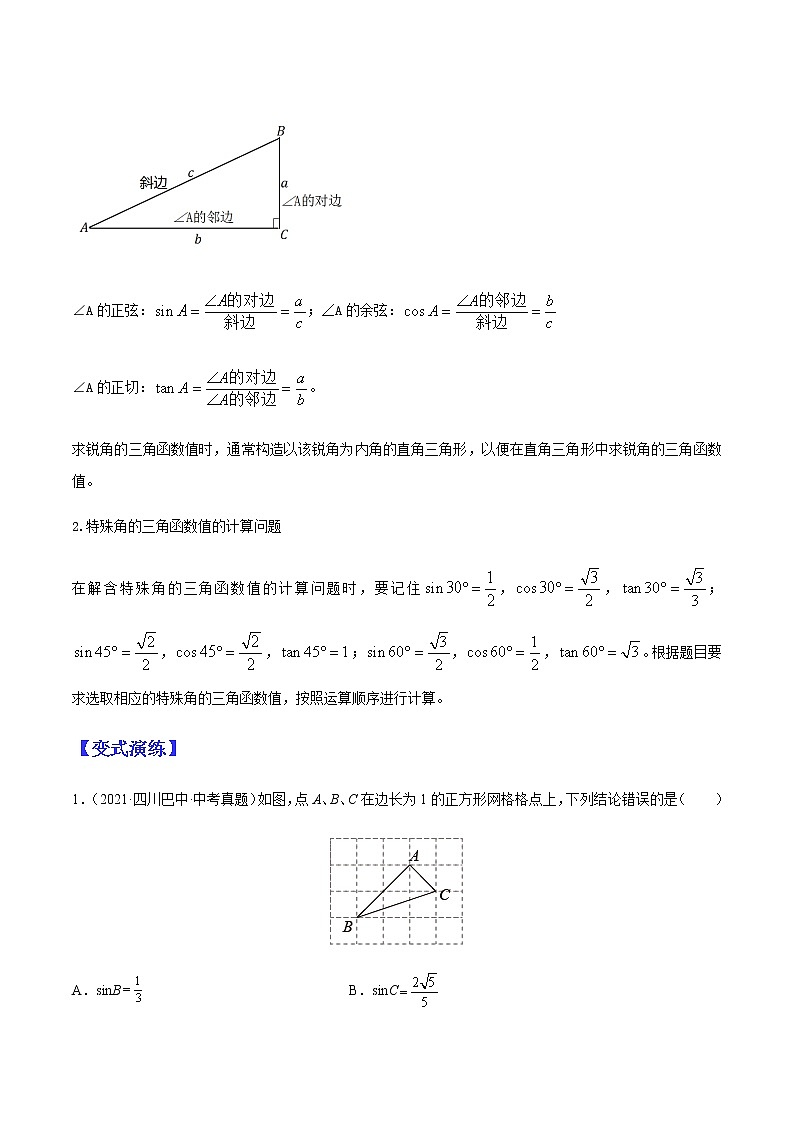
如图所示，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a，b，c。
∠A的正弦：；∠A的余弦：
∠A的正切：。
求锐角的三角函数值时，通常构造以该锐角为内角的直角三角形，以便在直角三角形中求锐角的三角函数值。
2.特殊角的三角函数值的计算问题
在解含特殊角的三角函数值的计算问题时，要记住，，；，，；，，。根据题目要求选取相应的特殊角的三角函数值，按照运算顺序进行计算。
【变式演练】
1．（2021·四川巴中·中考真题）如图，点A、B、C在边长为1的正方形网格格点上，下列结论错误的是（ ）
A．sinBB．sinC
C．tanBD．sin2B+sin2C＝1
【答案】A
【分析】根据勾股定理得出AB，AC，BC的长，进而利用勾股定理的逆定理得出△ABC是直角三角形，进而解答即可．
【解析】解：由勾股定理得：
,
∴△ABC是直角三角形，∠BAC=90°，
∴，，，，只有A错误．
故选择：A．
2．（2021·山东淄博·中考真题）如图，在中，是斜边上的中线，过点作交于点．若的面积为5，则的值为（ ）
A．B．C．D．
【答案】A
【分析】由题意易得，设，则有，则有，，然后可得，过点C作CH⊥AB于点H，进而根据三角函数及勾股定理可求解问题．
【解析】解：∵，，
∴，
∴，
∵是斜边上的中线，
∴，
设，则有，
∵，
∴由勾股定理可得，
∵的面积为5，
∴，
∵，
∴，即，化简得：，
解得：或，
当时，则AC=2，与题意矛盾，舍去；
∴当时，即，过点C作CH⊥AB于点H，如图所示：
∴，，，
∴，，
∴，
∴，
∴；
故选A．
3．（2021·四川宜宾·中考真题）如图，在△ABC中，点O是角平分线AD、BE的交点，若AB＝AC＝10，BC＝12，则tan∠OBD的值是（ ）
A．B．2C．D．
【答案】A
【分析】根据等腰三角形的性质，可得AD⊥BC，BD=BC=6，再根据角平分线的性质及三角的面积公式得，进而即可求解．
【解析】解：AB＝AC＝10，BC＝12， AD平分∠BAC，
∴AD⊥BC，BD=BC=6，
∴AD=，
过点O作OF⊥AB，
∵BE平分∠ABC，
∴OF=OD，
∵

∴，即：，解得：OD=3，
∴tan∠OBD=，
故选A．
【题型二】 利用锐角三角函数解决与三角形有关的问题
【典例分析】（2021·湖北襄阳·中考真题）如图，正方形的对角线相交于点，点在边上，点在的延长线上，，交于点，，，则______．
【答案】
【分析】作出如图所示的辅助线，利用SAS证明△ADH△ABF以及△EAF△EAH，在Rt△ABE中，利用勾股定理求得正方形的边长，再证明△BAF△OAG，即可求解．
【解析】解：如图，在CD上取点H，使DH=BF=2，连接EH、AH，
∵四边形ABCD是正方形，
∴∠ADH=∠ABC=∠ABF=90°，AD=AB，∠BAC=∠DAC=45°，
∴△ADH△ABF(SAS)，
∴∠DAH=∠BAF，AH=AF，
∵∠EAF=45°，即∠BAF+∠EAB=45°，
∴∠DAH+∠EAB=45°，则∠EAH=45°，
∴∠EAF=∠EAH=45°，
∴△EAF△EAH (SAS)，
∴EF=EH，
∵，
设BE=a，则AB=2a，EC=a，CH=2a-2，EF=EH=a+2，
在Rt△CEH中，,即，
解得：，
则AB=AD=6，BE=EC=3，
在Rt△ABE中，,
∴AE=3，
同理AF=2，
AO=AB=3，
∵BE∥AD，
∴，
∴AG=2，
∴，，
∴，
∵∠EAF=∠BAC=45°，
∴∠BAF=∠OAG，
∴△BAF△OAG，
∴，
∵∠GAF=∠OAB=45°，
∴△GAF是等腰直角三角形，
∴FG= AG=2，
故答案为：2．
【提分秘籍】
1.有关直角三角形的问题
求一个锐角的三角函数值时，应将这个锐角转化为直角三角形中的锐角，通常作垂线构造直角三角形或利用等角的传递性进行转化，再根据已知条件，确定解直角三角形的方法。2.有关非直角三角形的问题
非直角三角形包括锐角三角形和钝角三角形，解非直角三角形时常通过作高，把解非直角三角形问题转化成解直角三角形问题。
3.解非直角三角形的关键是作出三角形合适的高，构造直角三角形，通过解直角三角形求出线段的长或角的度数。
【变式演练】
1．（2021·江苏常州·中考真题）如图，在中，，D是上一点（点D与点A不重合）．若在的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点，则长的取值范围是________．
【答案】＜AD＜2
【分析】以AD为直径，作⊙O与BC相切于点M，连接OM，求出此时AD的长；以AD为直径，作⊙O，当点D与点B重合时，求出AD的长，进入即可得到答案．
【解析】解：以AD为直径，作⊙O与BC相切于点M，连接OM，则OM⊥BC，此时，在的直角边上存在3个不同的点分别和点A、D成为直角三角形，如图，
∵在中，，
∴AB=2，
∵OM⊥BC，
∴，
设OM=x，则AO=x，
∴，解得：，
∴AD=2×=，
以AD为直径，作⊙O，当点D与点B重合时，如图，此时AD=AB=2，
∴在的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点，则长的取值范围是：＜AD＜2．
故答案是：＜AD＜2．
2．（2021·四川眉山·中考真题）如图，在菱形中，，对角线、相交于点，点在线段上，且，点为线段上的一个动点，则的最小值是______．
【答案】
【分析】过M点作MH垂直BC于H点，与OB的交点为P点，此时的长度最小为MH，再算出MC的长度， 在直角三角形MPC中利用三角函数即可解得MH
【解析】过M点作MH垂直BC于H点，与OB的交点为P点，此时的长度最小
∵菱形中，
∴AB=BC=AC=10，△ABC为等边三角形
∴∠PBC=30°，∠ACB=60°
∴在直角△PBH中，∠PBH=30°
∴PH=
∴此时得到最小值，
∵AC=10，AM=3,
∴MC=7
又∠MPC=60°
∴MH=MCsin60°=
故答案为：
3．（2021·甘肃武威·中考真题）如图，在矩形中，是边上一点，是边的中点，，则________．
【答案】6
【分析】先利用直角三角形斜边上的中线等于斜边的一半求解 再利用锐角三角函数依次求解即可得到答案．
【解析】解： 是边的中点，，



矩形，



故答案为：
【题型三】 解直角三角形
【典例分析】（2021·山东青岛·中考真题）某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼的高度．如图所示，其中观景平台斜坡的长是20米，坡角为，斜坡底部与大楼底端的距离为74米，与地面垂直的路灯的高度是3米，从楼顶测得路灯项端处的俯角是．试求大楼的高度．
（参考数据：，，，，，）
【答案】96米
【分析】延长AE交CD延长线于M，过A作AN⊥BC于N，则四边形AMCN是矩形，得NC=AM，AN=MC，由锐角三角函数定义求出EM、DM的长，得出AN的长，然后由锐角三角函数求出BN的长，即可求解．
【解析】延长交于点，
过点作，交于点，
由题意得，，
∴四边形为矩形，
∴，.
在中，，
∴，，
∴，，
∴，
∴.
在中，，
∴，
∴，
∴，
∴.
答：大楼的高度约为96米.
【提分秘籍】
1.坡度（坡比）问题：解坡度（坡比）问题的关键是理解坡度（坡比）的概念，坡度（坡比)i是指斜坡的竖直高度h与水平宽度l的比值：（为坡角）。
2.方向角问题：方向角问题常以轮船在海上航行的形式出现，解题时需构造直角三角形求解。
3.仰角、俯角的问题：仰角、俯角问题常以测量物体高度的形式出现，解题时常通过作高，把问题转化为解直角三角形问题；解决与仰角、俯角有关的应用问题时，常借助仰角或俯角构造直角三角形，并通过解直角三角形求解。
【变式演练】
1．（2021·辽宁鞍山·中考真题）小明和小华约定一同去公园游玩，公园有南北两个门，北门A在南门B的正北方向，小明自公园北门A处出发，沿南偏东方向前往游乐场D处；小华自南门B处出发，沿正东方向行走到达C处，再沿北偏东方向前往游乐场D处与小明汇合（如图所示），两人所走的路程相同．求公园北门A与南门B之间的距离．（结果取整数．参考数据：，，，）
【答案】
【分析】作于E，于F，易得四边形BCFE是矩形，则，，设，则，在中利用含30度的直角三角形三边的关系得到，在中，，根据题意得到，求得x的值，然后根据勾股定理求得AE和BE，进而求得AB．
【解析】解：如图，作于E，于F，
，
四边形BCFE是矩形，
，，
设，则，
在中，，
，
在中，，
，
，
，
解得：，
，
，
，
，
由勾股定理得，
，
，
答：公园北门A与南门B之间的距离约为．
2．（2021·广西河池·中考真题）如图，小明同学在民族广场A处放风筝，风筝位于B处，风筝线AB长为，从A处看风筝的仰角为，小明的父母从C处看风筝的仰角为．
（1）风筝离地面多少m？
（2）AC相距多少m？（结果保留小数点后一位，参考数据：，，，，，）
【答案】（1）50；（2）128.6
【分析】（1）如图，过作，根据的正弦及的长即可求得即风筝的高度；
（2）分别根据的余弦以及的正切求得，进而求得．
【解析】（1）如图，过作
m，
风筝离地面50m
（2）
相距128.6m．
3．（2021·湖南湘潭·中考真题）万楼是湘潭历史上的标志性建筑，建在湘潭城东北湘江的下游宋家桥．万楼的外形设计既融入了皇家大院、一类寺庙的庄严典雅，也吸收了江南民居诸如马头墙、猫拱背墙、灰瓦等特色，而最为独特的还是万楼“九五至尊”的结构．
某数学小组为了测量万楼主楼高度，进行了如下操作，用一架无人机在楼基A处起飞，沿直线飞行120米至点B，在此处测得楼基A的俯角为60°，再将无人机沿水平方向向右飞行30米至点C，在此处测得楼顶D的俯角为30°，请计算万楼主楼的高度．（结果保留整数，，）
【答案】米．
【分析】利用俯角定义，结合正弦、正切的定义、含30°角的直角三角形的性质，分别解得的长，再计算AD的长即可．
【解析】解：在中，
中，
（米）
答：万楼主楼的高度为米．
1．（2021·山东省济南中学九年级期中）的值是（ ）
A．B．C．D．
【答案】C
【分析】由题意利用特殊角的三角函数的值，求出结果即可．
【解析】解：，
故选C．
2．（2022·安徽潜山·九年级期末）如图，由边长为1的小正方形组成的网格中，点A，B，C都在网格线的交点上，以AB为直径的⊙O经过点C，若点D在⊙O上，则tan∠ADC＝（ ）
A．B．C．D．
【答案】B
【分析】连接AC、BC，根据圆周角定理得∠ACB=90°，由tan∠ADC＝tan∠ABC求出答案．
【解析】解：连接AC、BC，
∵AB为⊙O的直径，
∴∠ACB=90°,
∵∠ABC=∠ADC，
∴tan∠ADC＝tan∠ABC＝，
故选：B．
．
3．（2021·广东禅城·二模）如图，A、B分别为反比例函数（x＜0），y＝（x＞0）图象上的点，且OA⊥OB，则tan∠ABO的值为（ ）
A．B．C．D．
【答案】A
【分析】如图，过A作AC⊥x轴于C，过B作BD⊥x轴于D，根据A、B在函数图象上可求出S△AOC＝4，S△BDO＝9，根据相似三角形的判定得出△BDO∽△OCA，根据相似三角形的性质得出，，求出的值，根据即可求出角的正切值．
【解析】解：如图，过A作AC⊥x轴于C，过B作BD⊥x轴于D
则∠BDO＝∠ACO＝90°
∵A、B分别为反比例函数（x＜0），（x＞0）图象上的点
∴S△AOC＝4，S△BDO＝9
∵∠AOB＝90°
∴∠BOD+∠DBO＝∠BOD+∠AOC＝90°
∴∠DBO＝∠AOC
∴△BDO∽△OCA
∴
∴
∴
故选：A．
4．（2022·江苏·泰州中学附属初中九年级期末）在平面直角坐标系xOy中，一次函数的图象与x轴、y轴的交点分别为A、B，则∠OAB的余弦值为（ ）
A．B．C．D．
【答案】D
【分析】先求得点A、B的坐标，表示出OA、OB的长，利用勾股定理求得AB的长，即可求得∠OAB的余弦值．
【解析】解：令x=0，y=b，令y=0，x=，
∴点A的坐标为(，0)，点B的坐标为(0，b)，
∴OA=、OB= b，
∴AB＝=，
∴=，
故选：D．
5．（2022·广西博白·九年级期末）如图，在扇形OAB中，∠AOB＝105°，半径OA＝6，将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上的点D处，折痕交OA于点C，则阴影部分的面积为（ ）
A．B．C．D．
【答案】C
【分析】连接，根据这特可知，，进而可得是等边三角形，则，进而求得的面积，根据阴影部分面积等于求解即可．
【解析】连接，如图，
将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上的点D处，
又
是等边三角形，
∠AOB＝105°，
半径OA＝6
阴影部分面积等于
故选C．
6．（2022·山东历下·九年级期末）我国航天事业捷报频传，天舟二号于2021年5月29日成功发射，震撼人心．当天舟二号从地面到达点A处时，在P处测得A点的仰角∠DPA为30°，A与P两点的距离为10千米；它沿铅垂线上升到达B处时，此时在P处测得B点的仰角∠DPB为45°，则天舟二号从A处到B处的距离AB的长为（ ）（参考数据：，）
A．2.0千米B．1.5千米C．2.5千米D．3.5千米
【答案】D
【分析】由含30°角的直角三角形的性质得AD=5（千米），再由锐角三角函数定义求出PD、BD的长，即可得出答案．
【解析】解：在Rt△APD中，∠DPA=30°，AP=10千米，∠ADP=90°，cs∠DPA=cs30°=，
∴AD=AP=×10=5（千米），PD=AP•cs30°=10×=5（千米），
在Rt△BPD中，tan∠DPB=tan45°=，
∴BD=PD•tan45°=5×1=5（千米），
∴AB=BD-AD=5-5≈8.5-5=3.5（千米），
故选：D．
7．（2022·江苏太仓·九年级期末）如图，在Rt△ABC中，∠C＝90°，AB＝5，AC＝3，则sinB等于（ ）
A．B．C．D．
【答案】D
【分析】根据锐角三角函数的正弦值进行求解即可．
【解析】解：由题意知
故选D．
8．（2022·湖南新邵·九年级期末）下列说法中正确的是（ ）
A．B．若为锐角，则
C．对于锐角，必有D．若为锐角，则
【答案】B
【分析】根据锐角三角函数的定义及性质、特殊角三角函数逐项判断即可．
【解析】A、，故说法不正确；B、对于任一锐角，这个角的正弦等于它的余角的余弦，即若为锐角，则，故说法正确；C、当β=60°时，，则，故说法不正确；D、当α=45°时，，故说法不正确；故选：B。
9．（2022·陕西·西北工业大学附属中学九年级期末）如图，在△ABC中，D是BC边上的中点，连接AD，把△ACD沿AD翻折，得到△ADC′，DC′与AB交于点E，连接BC′，若BD＝BC′＝2，AD＝3，则△ADE的面积为（ ）
A．B．C．D．
【答案】B
【分析】连接 ，过点A作AG⊥BC于点G，作EH⊥BC于点H，由翻折得DC=DC'，可证明BD=BC′=DC'，从而得△BDC'为等边三角形，求出，设，则EH=，，，再证明得代入相关数据得，再根据可求解．
【解析】解：连接，过点A作AG⊥BC于点G，作EH⊥BC于点H，如图，
∵D是AC边上的中点，
∴BD=CD
∵BD＝BC′＝2，
∴BC′=BD= DC
由翻折知，△ADC≌△ADC'，
∴DC=DC'
∴BD=BC′=DC'
∴△BDC'为等边三角形
∴∠BDC'=∠BC'D=∠C'BC=60°，
∴
∵△ADC≌△ADC'，
∴∠ADC=∠ADC'= ，
∵，
∴
∵
∴设，则EH=DH×
又
∴
∵
∴EH//AG
∴
∴
∵
∴
解得，
∴
又，
∴
故选：B
10．（2022·安徽舒城·九年级期末）如图，在△ABC中，∠ACB=90°，AC=BC=8，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE=5，则sin∠BFD的值为（ ）
A．B．C．D．
【答案】A
【分析】由题意得：△AEF≌△DEF，故∠EDF=∠A；由三角形的内角和定理及平角的知识问题即可解决．
【解析】解：∵在△ABC中，∠ACB=90°，AC=BC=8，
∴∠A=∠B，
由折叠的性质得到：△AEF≌△DEF，
∴∠EDF=∠A，
∴∠EDF=∠B，
∴∠CDE+∠BDF+∠EDF=∠BFD+∠BDF+∠B=180°，
∴∠CDE=∠BFD．
又∵AE=DE=5，
∴CE=8-5=3，
∴在直角△ECD中，sin∠CDE=，
∴sin∠BFD=．
故选：A．
11．（2022·山东莱芜·九年级期末）如图，某水库大坝的横断面是梯形，坝高，斜坡的坡比为，则斜坡（ ）
A．13mB．8mC．18mD．12m
【答案】A
【分析】根据斜坡BC的坡比为i=5：12和坝高，如图可求出BF的长度，在Rt△BCF中根据勾股定理可求出BC的长度．
【解析】如图，过点C作CF⊥AB，垂足为F．那么，
∵坝高，CF⊥AB，
∴DE=CF=5cm
又斜坡的坡比为
∴BF=12cm，
在Rt△BCF中
BC=
=
=13cm
12．（2021·广东宝安·一模）如图，正方形ABCD中，AC与BD交于点O，M是对角线AC上的一个动点，直线BM与直线AD交于点E，过A作AH垂直BE于点H，直线AH与直线BD交于点N，连接EN、OH，则下列结论：①BM＝AN；②OH平分∠MHN；③当EN∥OM时，BN2＝DN•DB；④当M为AO中点时，＝，正确结论的个数有（ ）
A．1个B．2个C．3个D．4个
【答案】C
【分析】由正方形的性质可证明△ADN≌△BAM，从而可得BM=AN，即可判断①正确；通过证明点A、B、O、H四点共圆，可得∠BAO＝∠BHO＝∠OHN=45°，可判断②正确；由点A，B，E，N四点共圆及已知易得△ABE≌△NBE，可得AE=EN，AB=BN，设AE=EN=DN=x，分别求出BN2，DN∙DB的值，可判定③错误；设OA＝BO＝a，利用勾股定理和锐角三角函数可求出AH，BM的长，可得，故可得④正确，即可求解．
【解析】∵四边形ABCD是正方形，
∴∠BAD＝90°，∠BAC＝∠ADB＝45°，AB＝AD，AC⊥BD，
∵AN⊥BE，
∴∠DAN+∠AEB＝∠AEB+∠ABE＝90°，
∴∠DAN＝∠ABE，
∴△ADN≌△BAM（ASA），
∴BM＝AN，故①正确；
∵∠AHB＝∠AOB＝90°，
∴点A，点B，点O，点H四点共圆，
∴∠BAO＝∠BHO＝45°，
∴∠BHO＝∠OHN＝45°，故②正确；
∵EN∥OM，
∴∠DEN＝∠OAD＝45°＝∠ADO，∠END＝∠AOD＝90°，
∴EN＝DN，∠BAD＝∠BNE＝90°，
∴点A，点B，点E，点N四点共圆，
∴∠EAN＝∠EBN，
∴∠ABE＝∠DBE，
在△ABE和△NBE中，
，
∴△ABE≌△NBE（AAS），
∴AE＝EN，AB＝BN，
设AE＝EN＝DN＝x，
∴DE＝x，
∴AD＝x+x＝AB＝BN，
∵BN2＝（x+x）2＝（3+2）x2，DN•DB＝x（x+x+x）＝（2+）x2，
∴BN2≠DN•DB，故③错误；
设OA＝BO＝a，
∵点M是AO中点，
∴AM＝OM＝a，
∴BM＝＝＝a，
∵点A，点B，点O，点H四点共圆，
∴∠OAN＝∠OBM，
∴cs∠OBM＝cs∠OAN＝，
∴＝，
∴AH＝a，
∴＝，故④正确，
故选：C．
13．（2022·山东黄岛·九年级期末）计算：______．
【答案】-1
【分析】将各特殊角三角函数值代入计算即可得到答案．
【解析】解：

=
=
=-1
故答案为：-1
14．（2021·广东·东莞市翰林实验学校一模）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，tan∠DCB＝，AC＝12，则BC=___．
【答案】9
【分析】根据直角三角形的性质、同角的余角相等得到∠BCD=∠A，根据正切的定义计算即可
【解析】解：∵∠ACB=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠A，
在Rt△ACB中，
∵tanA=tan∠BCD==，
∴BC=AC=×12=9．
故答案为：9．
15．（2022·江苏·泰州中学附属初中九年级期末）已知α、β为锐角，若，，利用下列边长均为1的小正方形组成的网格图（如图），可求得tan（α+β）＝_____．
【答案】2
【分析】先证明，，得到tan（α+β）=tan，利用勾股定理的逆定理判断出△ABC是直角三角形，进一步计算即可求得答案．
【解析】解：如图，
BD=2，AD=1，BE=4，CE=3，
∴，，
∴，，
∴tan（α+β）=tan，
∵AB=，AC=，BC=，
，
∴,
∴△ABC是直角三角形，且90°，
∴tan（α+β）=tan==2，
故答案为：2．
16．（2022·福建省福州第一中学九年级期末）如图，以矩形ABCD的顶点A为圆心，适当长为半径作弧，分别交AB，AC于点M，N；再分别以点M，N为圆心，大于的长为半径作弧，两弧交于点P；作射线AP，交BC于点E，连接DE，交AC于点F．若，，则DF的长为______．
【答案】
【分析】先求解 再求解 再证明可得从而可得答案.
【解析】解： 矩形ABCD，，，



由作图可得：平分








故答案为：
17．（2021·广东龙湖·一模）如图，把矩形ABCD沿EF对折，使B与D重合，折痕EF交BD于G，连AG，若tan∠AGE＝，BF＝8，P为DG上一个动点，则PF+PC的最小值为_____．
【答案】10
【分析】如图，连接BE，CE，PE，取BE的中点O，连接OA，OG．首先证明△EGD≌△FGB（ASA），推出BF=DE=8，EG=FG，再证明PF=PE，推出PF+PC=PE+PC≥EC，想办法求出EC即可解决问题．
【解析】解：如图，连接BE，CE，PE，取BE的中点O，连接OA，OG．
由题意，EF垂直平分线段BD，
∴EB=ED，BG=GD，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EDG=∠FBG，
∵∠EGD=∠FGB，
∴△EGD≌△FGB（ASA），
∴BF=DE=8，EG=FG，
∵DB⊥EF，
∴PE=PF，
∴PF+PC=PE+PC≥EC，
∵∠BAE=∠BGE=90°，OB=OE，
∴OA=OB=OE=OG，
∴A，B，G，E四点共圆，
∴∠ABE=∠AGE，
∴tan∠ABE=tan∠AGE==，
设AE=k，AB=3k，
∵AB2+AE2=BE2，BE=DE=8，
∴（k）2+（3k）2=82，
∴k=2，
∴AB=CD=6，
∵∠EDC=90°，
∴EC==10，
∴PF+PC≥10，
∴PF+PC的最小值为10．
故答案为：10．
18．（2022·山东中区·九年级期末）如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，E为AC边上的中点，连接BE交AD于F，将△AFE沿若AC翻折到△AGE，若四边形AFEG恰好为菱形，连接BG，则tan∠ABG=________．
【答案】
【分析】过点G作GH⊥AB，交BA延长线于H，设AE=x，则AC=2x，由菱形的性质得出AF=EF，再证AF=BF=EF与△BAE∽△CAB，求出AB=x，BE=x，AF=EF=x，然后由菱形性质得AG=BE，证△BAE∽△AHG，求出AH=x，HG=，最后由锐角三角函数定义即可得出结果．
【解析】解：过点G作GH⊥AB，交BA延长线于H，如图所示：
设AE=x，则AC=2x，
∵四边形AFEG为菱形，
∴AF=EF，
∴∠FAE=∠FEA，
∵∠BAE=90°，
∴∠FAE+∠FAB=∠FEA+∠FBA=90°，
∴∠FAB=∠FBA，
∴AF=BF，
∴AF=BF=EF，
∵∠FBA+∠AEB=90°，∠FAB+∠ABD=90°，
∴∠ABD=∠AEB，
又∵∠BAE=∠BAC=90°，
∴△BAE∽△CAB，
∴，
∴AB2=AE•AC=2x2，
∴AB=x，
∴BE=，
∴AF=EF=x，
∵四边形AFEG是菱形，
∴AG∥BE，AG=AF=BF=EF，
∴∠HAG=∠ABE，AG=BE，
又∵∠H=∠BAE=90°，
∴△BAE∽△AHG，
∴，
∴AH=AB=x，HG=AE=，
∴BH=AH+AB=x+x=x，
∴，
故答案为：．
19．（2022·浙江东阳·九年级期末）计算：（﹣1）2022＋﹣4sin45°＋|﹣2|．
【答案】3
【分析】先计算乘方、化简平方根、计算特殊角的三角函数值、去绝对值，再进行合并即可．
【解析】原式
．
20．（2021·广东禅城·二模）计算：．
【答案】
【分析】直接利用特殊角的三角函数值以及零指数幂的性质、负整数指数幂的性质、绝对值的性质分别化简得出答案．
【解析】原式＝
＝．
故答案为：.
21．（2022·重庆巴蜀中学九年级开学考试）图（1）为某大型商场的自动扶梯．图（2）中的AB为从一楼到二楼的扶梯的侧面示意图．小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（）向正前方走了2m，发现日光灯C刚好在他的正上方．已知自动扶梯AB的坡度为1：2.4，AB的长度是13m，（参考数据：sin37°≈0.6，cs37°＝0.8，tan37°≈0.75）．
(1)求图中B到一楼地面的高度．
(2)求日光灯C到一楼地面的高度．（结果精确到十分位）．
【答案】(1)图中B到一楼地面的高度为
(2)日光灯到一楼地面的高度为
【分析】（1）过点作于、交于，过点作于，过点作于、交于，如图（2）所示：则，四边形、四边形是矩形，，，，，设，的坡度为，在中，由勾股定理得：，解得：，即可求得；
（2）由（1），得出，在中，利用，求出，求出．
【解析】(1)解：过点作于、交于，过点作于，过点作于、交于，如图（2）所示：
则，四边形、四边形是矩形，，
，，，
设，
的坡度为，
，
，
在中，由勾股定理得：，
解得：，
，
答：图中B到一楼地面的高度为；
(2)解：，
，
在中，，
，
，
，即日光灯到一楼地面的高度为．
22．（2022·山东黄岛·九年级期末）如图1是一个手机支架，图2是其侧面示意图，，可分别绕点，转动，经测量，，．当，转动到，时，求点到的距离．（结果保留小数点后一位）
参考数据：，，，，，，．
【答案】点到的距离为6.3cm
【分析】过点作于点，延长交于点，过点作于点，根据，可求出BD的长度，根据三个内角之和为180°可知，，进而根据可求出CN的长度，进而根据，可求出CM的长度．
【解析】过点作于点，延长交于点，过点作于点，
在中，，，
∵，
∴，
∵，
∴，
在中，，，
∵，
∴，
∴，
在中，，，
∵，
∴，
答：点到的距离为6.3cm．
23．（2021·河北新乐·九年级期末）如图，在⊙O中，AB是直径，弦；垂足为H，E为上一点，F为弦DC延长线上一点，连接FE并延长交直径AB的延长线于点G，连接AE交CD于点P，若．
(1)求证：FE是⊙O的切线；
(2)若⊙O的半径为8，，求BG的长．
【答案】(1)见解析 (2)2
【分析】（1）由等腰三角形的性质可得∠A=∠AEO，∠FPE=∠FEP，由余角的性质可求∠FEP+∠AEO=90°，可得结论；
（2）由余角的性质可求∠F=∠EOG，由锐角三角函数可设EG=3x，OG=5x，在Rt△OEG中，利用勾股定理可求x=2，即可求解．
【解析】(1)证明：连接OE，如图，
∵，∴．
∵，∴．
∵，∴，∴．
∵，∴．∴．
∴，∴，∴．
∵OE是⊙O的半径，∴EF是圆的切线．
(2)解：∵，∴是直角三角形．
∵，∴．设，则．
由勾股定理得，．
由（1）得，是直角三角形，
∴，∴，即．
∵，
∴，解得．
24．（2022·山东历城·九年级期末）如图，在Rt△ABC中，，D是AB上的一点，以AD为直径的⊙O与BC相切于点E，连接AE，DE．
(1)求证：AE平分∠BAC；
(2)若，求的值．
【答案】(1)见解析
(2)
【分析】（1）连接OE，根据切线的性质得到∠OEB=90°，进而得到OE//AC，根据平行线的性质得到∠OEA=∠EAC，根据等腰三角形的性质得到∠OEA=∠OAE，根据角平分线的定义证明结论；
（2）根据圆周角定理得到∠AED=90°，证明△DAE∽△EAC，根据相似三角形的性质得到，根据余弦的定义计算，得到答案．
【解析】(1)证明：连接OE，
∵BC是⊙O的切线，
∴OE⊥BC，即∠OEB=90°，
∵∠C=90°，
∴OE//AC，
∴∠OEA=∠EAC，
∵OE=OA，
∴∠OEA=∠OAE，
∴∠OAE=∠EAC，即AE平分∠BAC；
(2)∵AD为⊙O的直径，
∴∠AED=90°，
∵∠OAE=∠EAC，∠C=90°，
∴△DAE∽△EAC，
∴，
∵∠C=90°，∠B=30°，
∴∠BAC=90°-30°=60°，
∴∠DAE=∠BAC=30°，
∵，
∴．
25．（2022·湖南衡阳·九年级期末）如图，已知抛物线经过点A(﹣1，0)，B(3，0)，C(0，﹣3)三点．点D为抛物线的顶点．连接AC，BC，CD，BD．
(1)求抛物线的解析式和D点坐标；
(2)求证：△AOC∽△DCB；
(3)如图1，延长AC，BD相交于点E，求tan∠AEB的值．
(4)如图2，点P为抛物线在第四象限内的一个动点，过点P作PM⊥直线CD，垂足为M，当PM最大时，请直接写出此时点P的坐标．
【答案】(1)y＝x2﹣2x﹣3，(1，﹣4)(2)见解析
(3)1
(4)(，﹣)
【分析】（1）先由点A和点B的坐标设二次函数的交点式，然后代入点C的坐标求得二次函数的解析式，再将函数解析式化为顶点式求得点D的坐标；
（2）由点A、B、C、D的坐标求得OA、OC、AC、BC、BD、CD的长，然后证明三角形相似；
（3）先求得直线AC和直线BD的解析式，然后求得点E的坐标，进而求得AE和BE的长，过点B作BF⊥AE于点F，过点E作EG⊥x轴于点G，然后利用等面积法求BF得长，进而利用勾股定理求得EF的长，最后求得tan∠AEB的值；
（4）先求直线BC的解析式，过点P作PH⊥x轴交BC于点H，然后设点P的坐标，得到点H的坐标，从而得到PH的长度，再利用等面积法求得PM的长度，最后利用二次函数的性质求得PM最大时，点P的坐标．
【解析】(1)由抛物线经过点A（﹣1，0）和B（3，0）设y＝a（x+1）（x﹣3），
将点C（0，﹣3）代入y＝a（x+1）（x﹣3）得，﹣3a＝﹣3，
∴a＝1，
∴y＝（x+1）（x﹣3）＝x2﹣2x﹣3=（x﹣1）2﹣4，
∴点D的坐标为（1，﹣4）；
(2)∵A（﹣1，0），B（3，0），C（0，﹣3），D（1，﹣4），
∴OA＝1，OC＝3，AC＝，BC＝=3，BD＝ =2，CD＝，
∴，
∴△AOC∽△DCB；
(3)设直线AC的解析式为y＝kx+b，则
，解得：，
∴直线AC的解析式为y＝﹣3x﹣3，
设直线BD的解析式为y＝mx+n，则
3m+n=0m+n=−4，解得：，
∴直线BD的解析式为y＝2x﹣6，
联立y＝﹣3x﹣3和y＝2x﹣6得，
，解得：，
∴点E的坐标为（，﹣），
∵A（﹣1，0），B（3，0），
∴AE＝，BE＝，AB＝4，
如图1，过点B作BF⊥AE于点F，过点E作EG⊥x轴于点G，则EG＝，
∵S△ABE＝，
∴，
解得：BF＝，
∴EF＝＝，
∴tan∠AEB＝＝1；
(4)设直线BC的解析式y＝kx+b，则
，解得：，
∴直线BC的解析式为y＝x﹣3，
如图2，过点P作PH⊥x轴交BC于点H，连接PC，PB，
设点P的坐标为（x，x2﹣2x﹣3），则点H的坐标为（x，x﹣3），
∴PH＝x﹣3﹣（x2﹣2x﹣3）＝﹣x2+3x，
∵PM⊥直线CD，
∴S△PBC＝，
∴×3×PM＝×（﹣x2+3x）×3，
∴PM＝﹣＝﹣（x﹣）2+，
∴当x＝时，PM最大＝，
此时，点P的坐标为（，﹣）．
26．（2021·湖南·师大附中梅溪湖中学二模）已知△ABC中，F、D分别为边AC、BC上的点，过点F、D分别作AC、BC的垂线交于一点I且IF＝ID．
(1)求证：FC＝DC；
(2)如图1，IA为△ABC的角平分线，点F为AC中点，当AF＝2，BD＝4时，求sin∠BAC的值；
(3)如图2，若过点I作IG⊥AB于点G，且IG＝IF＝GA＝2，∠B＝30°，求△ABC的周长．
【答案】(1)见解析．
(2)．
(3)．
【分析】（1）由题意得，，又由，，可证得，即可得出结论．
（2）由为的角平分线得到，又，点F为AC中点，则垂直平分，得，所以，由得，得到，故为等腰三角形，B、I、E三点共线，连接BI.，在中，，由勾股定理得到的长，即可求得sin的值．
（3）连接，，由，且，得到平分，由，得，则，进一步得到四边形AGIF是正方形，，，，在中，可求，进而求得的长，进一步求得、的长，即可求得的周长．
【解析】(1)证明：由题意得到，
∴
在和中，
∵

∴（）
∴
(2)解：如图3，连接，
∵为的角平分线
∴
∵，点F为AC中点
∴垂直平分
∴
∴
∵
∴
∴
∴为等腰三角形
∴B、I、E三点共线
在中，
由勾股定理得
∴sin
故答案为：．
(3)
如图4，连接，，
∵，且
∴平分
∵
∴为等腰直角三角形
∴
∴
∴四边形 AGIF是正方形
∴
∵
∴
∵，且
∴平分
∴
在中，
∴
∴
在中，，
∴
∴的周长为．
故答案为：．