专题08图形的变换-2022年中考数学二轮热点题型归纳与变式演练试卷（学生版+教师版）

这是一份专题08图形的变换-2022年中考数学二轮热点题型归纳与变式演练试卷（学生版+教师版），文件包含专题08图形的变换教师版docx、专题08图形的变换学生版docx等2份试卷配套教学资源，其中试卷共99页， 欢迎下载使用。
一、热点题型归纳
【题型一】 轴对称图形与中心对称图形的概念
【题型二】平移与旋转的作图问题
【题型三】 平移与旋转中的计算问题
二、最新模考题组练2
【题型一】轴对称图形与中心对称图形的概念
【典例分析】（2021·辽宁鞍山·中考真题）下列四幅图片上呈现的是垃圾类型及标识图案，其中标识图案不是轴对称图形的是（ ）
A．B．
C．D．
【提分秘籍】
轴对称图形和中心对称图形的辨别
1.如果一个平面图形沿一条直线折叠，直线两旁的部分能够完全重合，这个图形叫做轴对称图形，这条直线就是它的对称轴。也说这个图形关于这条直线（成轴）对称。
2.把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。
3.在判断一个图形是否为轴对称图形、中心对称图形时，要明确以下两点：
①如果能找到一条直线（对称轴）把一个图形分成两部分，且直线两旁的部分完全重合，那么这个图形就是轴对称图形；
②把一个平面图形绕某一点旋转180°，如果旋转后的图形能和原图形重合，那么这个图形就是中心对称图形。
【变式演练】
1．（2021·青海西宁·中考真题）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．三角形B．等边三角形
C．平行四边形D．菱形
2．（2021·山东济南·中考真题）以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
3．（2021·江苏徐州·中考真题）下列图形，是轴对称图形但不是中心对称图形的是（ ）
A．B．
C．D．
【题型二】平移与旋转的作图问题
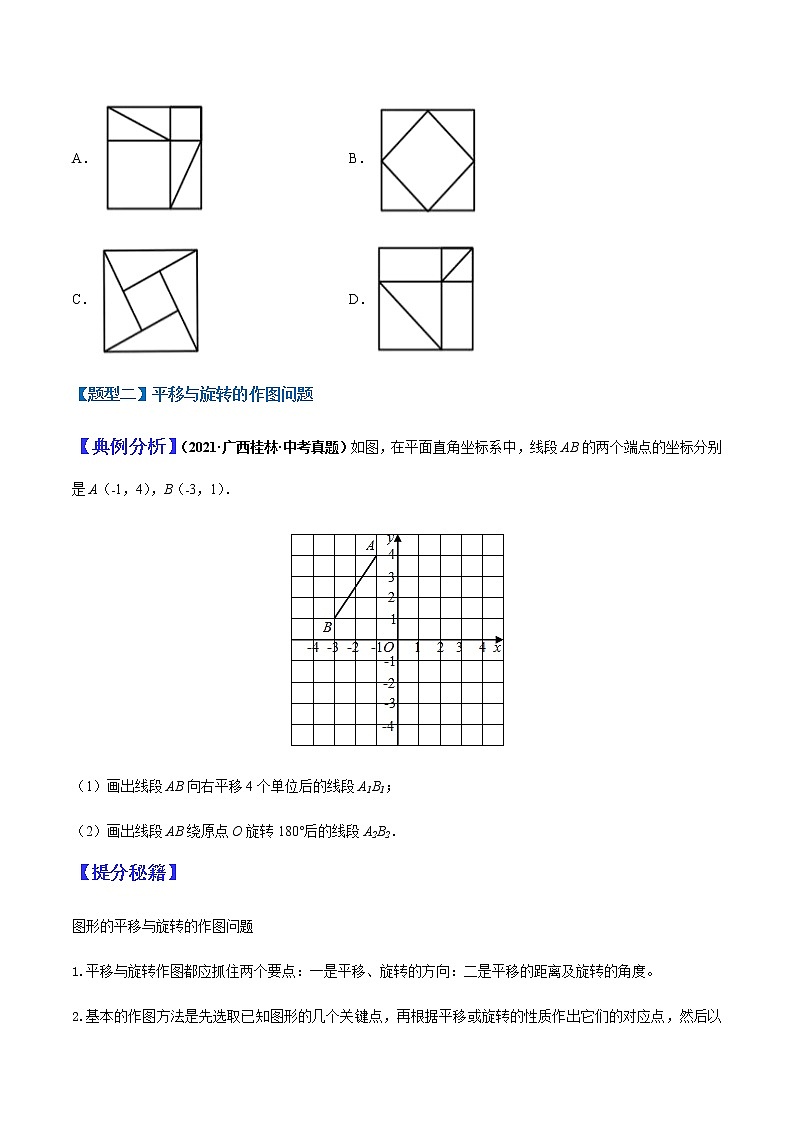
【典例分析】（2021·广西桂林·中考真题）如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A（﹣1，4），B（﹣3，1）．
（1）画出线段AB向右平移4个单位后的线段A1B1；
（2）画出线段AB绕原点O旋转180°后的线段A2B2．
【提分秘籍】
图形的平移与旋转的作图问题
1.平移与旋转作图都应抓住两个要点：一是平移、旋转的方向：二是平移的距离及旋转的角度。
2.基本的作图方法是先选取已知图形的几个关键点，再根据平移或旋转的性质作出它们的对应点，然后以“局部带动整体”的思想方法作出变换后的图形。
无论是平移还是旋转，都不改变图形的大小和形状。
【变式演练】
1．（2020·四川巴中·中考真题）如图所示，△ABC在边长为1cm的小正方形组成的网格中．
（1）将△ABC沿y轴正方向向上平移5个单位长度后，得到，请作出，并求出的长度；
（2）再将绕坐标原点O顺时针旋转180°，得到，请作出，并直接写出点的坐标；
（3）在（1）（2）的条件下，求线段AB在变换过程中扫过图形的面积和．
2．（2021·四川达州·中考真题）如图，在平面直角坐标中，的顶点坐标分别是，，．
（1）将以为旋转中心旋转，画出旋转后对应的；
（2）将平移后得到，若点的对应点的坐标为，求的面积
3．（2021·江苏淮安·中考真题）如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．
（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；
（2）连接CC1，△ACC1的面积为 ；
（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的．
【题型三】平移与旋转中的计算问题
【典例分析】（2011·山东临沂·中考真题）阅读下面材料：
小伟遇到这样一个问题，如图1，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O．若梯形ABCD的面积为1，试求以AC，BD，AD+BC的长度为三边长的三角形的面积．
小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可．他先后尝试了翻折，旋转，平移的方法，发现通过平移可以解决这个问题．他的方法是过点D作AC的平行线交BC的延长线于点E，得到的△BDE即是以AC，BD，AD+BC的长度为三边长的三角形（如图2）．
参考小伟同学的思考问题的方法，解决下列问题：
如图3，△ABC的三条中线分别为AD，BE，CF．
（1）在图3中利用图形变换画出并指明以AD，BE，CF的长度为三边长的一个三角形（保留画图痕迹）；
（2）若△ABC的面积为1，则以AD，BE，CF的长度为三边长的三角形的面积等于_____．
【提分秘籍】
有关图形的平移与旋转的计算问题
1.在平面内，将一个图形沿某个方向移动一定的距离，这种图形变换就是平移。
2.图形平移具有以下性质：经过平移，对应点所连的线段平行（或在同一条直线上）且相等，对应线段平行（或在同一条直线上)且相等，对应角相等。
3.把一个平面图形绕着平面内某一点O转动一个角度，这种图形变换称为图形的旋转。
4.图形旋转具有以下性质：
①对应点到旋转中心的距离相等；
②对应点与旋转中心所连线段的夹角等于旋转角；
③旋转前后的图形全等.图形的平移和旋转都不改变图形的形状和大小。
5.解图形的平移问题时，一要弄清平移的方向，二要注意平移的距离；解图形的旋转问题时，要注意图形旋转的三要素（旋转方向、旋转中心、旋转角度）和性质。
【变式演练】
1．（2021·山东日照·中考真题）问题背景：
如图1，在矩形中，，，点是边的中点，过点作交于点．
实验探究：
（1）在一次数学活动中，小王同学将图1中的绕点按逆时针方向旋转，如图2所示，得到结论：①_____；②直线与所夹锐角的度数为______．
（2）小王同学继续将绕点按逆时针方向旋转，旋转至如图3所示位置.请问探究（1）中的结论是否仍然成立？并说明理由．
拓展延伸：
在以上探究中，当旋转至、、三点共线时，则的面积为______．
2．（2021·辽宁朝阳·中考真题）如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O逆时针旋转90°，交射线CB于点N．
（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；
（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；
（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且＜，请直接写出的值（用含k的式子表示）．
3．（2021·江苏徐州·中考真题）如图1，正方形的边长为4，点在边上（不与重合），连接．将线段绕点顺时针旋转90°得到，将线段绕点逆时针旋转90°得到．连接．
（1）求证：
①的面积；
②；
（2）如图2，的延长线交于点，取的中点，连接，求的取值范围．
1．（2021·江苏句容·九年级期中）如图，将边长为6个单位的正方形ABCD沿其对角线BD剪开，再把△ABD沿着DC方向平移，得到△A′B′D′，当两个三角形重叠部分的面积为4个平方单位时，它移动的距离DD′等于（ ）
A．2B．C．D．
2．（2022·重庆·一模）在平面直角坐标系中，将点先向左平移个单位得点，再将向上平移个单位得点，若点落在第三象限，则的取值范围是（ ）
A．B．C．D．或
3．（2021·山东·枣庄市台儿庄区教育局教研室九年级期中）如图，将△ABC沿BC边向右平移得到△DEF，DE交AC于点G．若BC：EC＝3：1．S△ADG＝16．则S△CEG的值为（ ）
A．2B．4C．6D．8
4．（2022·内蒙古乌兰察布·九年级期末）在如图所示标志中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
5．（2022·安徽潜山·九年级期末）下列交通标识中，不是轴对称图形，是中心对称图形的是（ ）
A．B．C．D．
6．如图，在△ABC中，∠BAC＝90°，AB=AC=5cm，点D为△ABC内一点，∠BAD＝15°，AD=3cm，连接BD，将△ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，连接DE，交AC于点F，则CF的长为（ ）cm．
A．B．4﹣C．5﹣D．6﹣
7．（2022·广东·新丰县教育局教研室九年级期末）如图，将△ABC绕点顺时针旋转60°得到△AED，若，则等于（ ）
A．2cmB．3cmC．4cmD．5cm
8．（2021·福建·闽江学院附中九年级期中）如图，在△ABC中，AB＝4，BC＝7.6，∠B＝60°，将△ABC绕点A顺时针旋转到△ADE，当点B的对应点D恰好落在BC边上时，CD的长为（ ）
A．3.6B．3.9C．4D．4.6
9．（2022·安徽合肥·九年级期末）如图，中，，，若将绕点逆时针旋转得到，连接，则在点运动过程中，线段的最小值为（ ）
A．1B．C．D．2
10．（2021·广东阳东·一模）如图，四边形为正方形，的平分线交于点，将绕点顺时针旋转得到，延长交于点，连接，与相交于点．有下列结论：①；②；③；④，其中正确的是（ ）
A．①②B．②③C．①②③D．①②③④
11．（2022·江苏无锡·九年级期末）如图，在Rt△ABC中，，，点D、E分别是AB、AC的中点．将△ADE绕点A顺时针旋转60°，射线BD与射线CE交于点P，在这个旋转过程中有下列结论：①△AEC≌△ADB；②CP存在最大值为；③BP存在最小值为；④点P运动的路径长为．其中，正确的（ ）
A．①②③B．①②④C．①③④D．②③④
12．（2022·辽宁鞍山·九年级期末）如图，在中，，点为边上一点，将沿直线翻折得到，与边交于点E，若，点为中点，，则的长为（ ）
A．B．6C．D．
13．（2022·重庆大渡口·九年级）如图，将△ABC沿BC边上的中线AD平移到的位置，已知△ABC的面积为18，阴影部分三角形的面积为2．若，则等于______．
14．（2021·江苏·无锡市江南中学九年级期中）如图，将边长为4的正方形ABCD沿对角线AC剪开，再把△ABC沿着AD方向平移得到△A′B′C′，若两个三角形重叠部分的面积为3，则它移动的距离AA′等于 ___；移动的距离AA′等于 ___时，两个三角形重叠部分面积最大．
15．（2021·广东宝安·一模）如图，在菱形ABCD中，∠A＝60°，E为AD边上的一个动点，连接BE，将AB沿着BE折叠得到A'B，A的对应点为A'，连接A'D，当A′B⊥AD时，∠A'DE的度数为 ______．
16．（2022·上海闵行·九年级期末）如图， 在 Rt △ABC 中， ， 点 是 边上一点，将 沿着过点 的一条直线翻折，使得点 落在边 上的点 处，联结 ， 如果 ， 那么 的长为______
17．（2021·重庆市渝北区实验中学校九年级期中）如图，在Rt△ABC中，∠ACB＝90°，点D是边AB的中点，连接CD，将△BCD沿直线CD翻折得到△ECD，连接AE．若AC＝6，BC＝8，则△ADE的面积为____．
18．（2022·广东潮安·九年级期末）如图，△ABC和都是等边三角形，，，固定△ABC，把绕点C旋转任意角度，连接AD，BE，设AD，BE所在的直线交于点O，则在旋转过程中，始终有，且的大小保持不变，这时点O到直线AB的最大距离为______．
19．（2021·北京昌平·九年级期中）如图是边长为1的正方形网格，△A1B1C1的顶点均在格点上．
(1)在该网格中画出△A2B2C2（△A2B2C2的顶点均在格点上），使△A2B2C2∽△A1B1C1；
(2)说明△A2B2C2和△A1B1C1相似的依据，并直接写出∠B2A2C2的度数．
20．（2021·福建·龙岩二中九年级期中）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（﹣1，0），B（﹣4，1），C（﹣2，2）．
（1）直接写出点B关于原点对称的点B′的坐标： ；
（2）平移△ABC，使平移后点A的对应点A1的坐标为（2，1），请画出平移后的△A1B1C1；
（3）画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2．
21．（2022·辽宁建昌·九年级期末）如图，在边长为1的正方形组成的网格中建立直角坐标系，的顶点均在格点上，点为原点，点，的坐标分别是，．
(1)若将△AOB向下平移3个单位，则点B的对应点坐标为______；
(2)将△AOB绕点逆时针旋转后得到，请在图中作出，并求出这时点的坐标为______；
(3)求旋转过程中，线段扫过的图形的弧长．
22．（2022·安徽全椒·九年级期末）△ABC在边长为1的正方形网格中如图所示
（1）以点C为位似中心，作出△ABC的位似图形，使△ABC与的位似比为1：2，且位于点C的异侧；
（2）作出△ABC绕点C顺时针旋转90°后的图形；
23．（2021·广东阳东·一模）如图，在△ABD中，∠ABD＝∠ADB．
(1)作点A关于BD的对称点C；（用尺规作图，保留作图痕迹，不要求写作法）
(2)在（1）所作的图中，连接BC，DC．求证：四边形ABCD是菱形．
24．（2022·甘肃崆峒·九年级期末）图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABO的三个顶点坐标分别为，，．
（1）画出△ABO关于x轴对称的；
（2）画出△ABO绕点O顺时针旋转90°后得到的．
25．（2021·天津河西·九年级期中）如图，在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA=90°，BO=BA，顶点A（4，0），点B在第一象限，矩形OCDE的顶点E（，0），点C在y轴的正半轴上，点D在第二象限，射线DC经过点B．
（Ⅰ）求点的坐标；
（Ⅱ）将矩形沿轴向右平移，得到矩形，点，，，的对应点分别为，，，．设，矩形与△OAB重叠部分的面积为．
①当时，试用含有的式子表示，并直接写出的取值范围；
②矩形沿轴向右平移的过程中，求面积的最大值（直接写出结果即可）．
26．（2022·黑龙江省八五四农场学校九年级期末）如图，矩形OABC在平面直角坐标系中，OC、OA是x2﹣12x+32＝0的两根，OC＞OA．
(1)求B点的坐标．
(2)把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，使D、C、B、P四点形成的四边形为平行四边形？若存在，请直接写出P点坐标，请说明理由．
27．（2021·重庆巴南·九年级期末）如图，在△ABC中，∠BAC＝90°，AB＝AC，点D为线段AB上一点，线段CD绕点C逆时针旋转90°能与线段CE重合，点F为AC与BE的交点．
(1)若BC＝5，CE＝4，求线段BD的长；
(2)猜想BD与AF的数量关系，并证明你猜想的结论；
(3)设CA＝3DA＝6，点M在线段CD上运动，点N在线段CA上运动，运动过程中，DN+MN的值是否有最小值，如果有，请直接写出这个最小值；如果没有，请说明理由．
28．（2021·北京市师达中学九年级）如图1，在正方形ABCD中，点F在边BC上，过点F作EF⊥BC，且FE＝FC（CE＜CB），连接CE、AE，点G是AE的中点，连接FG．
(1)用等式表示线段BF与FG的数量关系： ；
(2)将图1中的△CEF绕点C按逆时针旋转，使△CEF的顶点F恰好在正方形ABCD的对角线AC上，点G仍是AE的中点，连接FG、DF．
①在图2中，依据题意补全图形；
②用等式表示线段DF与FG的数量关系并证明．
29．（2022·安徽潜山·九年级期末）如图，△ABC中，∠BAC＝120°，以BC为边向外作等边△BCD，延长AC到E，使CE＝BA，连接DE．
(1)△DCE可以由△DBA经过怎样的旋转得到，并说明理由；
(2)记BC，AD相交于点F．
①求证：∠DCF＝∠DAE；
②已知等边△BCD的边长为6，AC+AB＝8，求AF的长．
30．（2022·山东天桥·九年级期末）（1）如图1，正方形ABCD与调研直角△AEF有公共顶点A，∠EAF＝90°，连接BE、DF，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，则＝________；β＝________；
（2）如图2，矩形ABCD与Rt△AEF有公共顶点A，∠EAF＝90°，且AD＝2AB，AF＝2AE，连接BE、DF，将Rt△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，请求出的值及β的度数，并结合图2进行说明；
（3）若平行四边形ABCD与△AEF有公共项点A，且∠BAD＝∠EAF＝α(0°＜α＜180°)，AD＝kAB， AF＝kAE(k≠0)，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的锐角的度数为β，则：
①＝________；
②请直接写出α和β之间的关系式．