初中数学华师大版八年级下册2. 矩形的判定教学设计

这是一份初中数学华师大版八年级下册2. 矩形的判定教学设计，共4页。
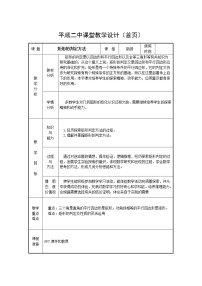
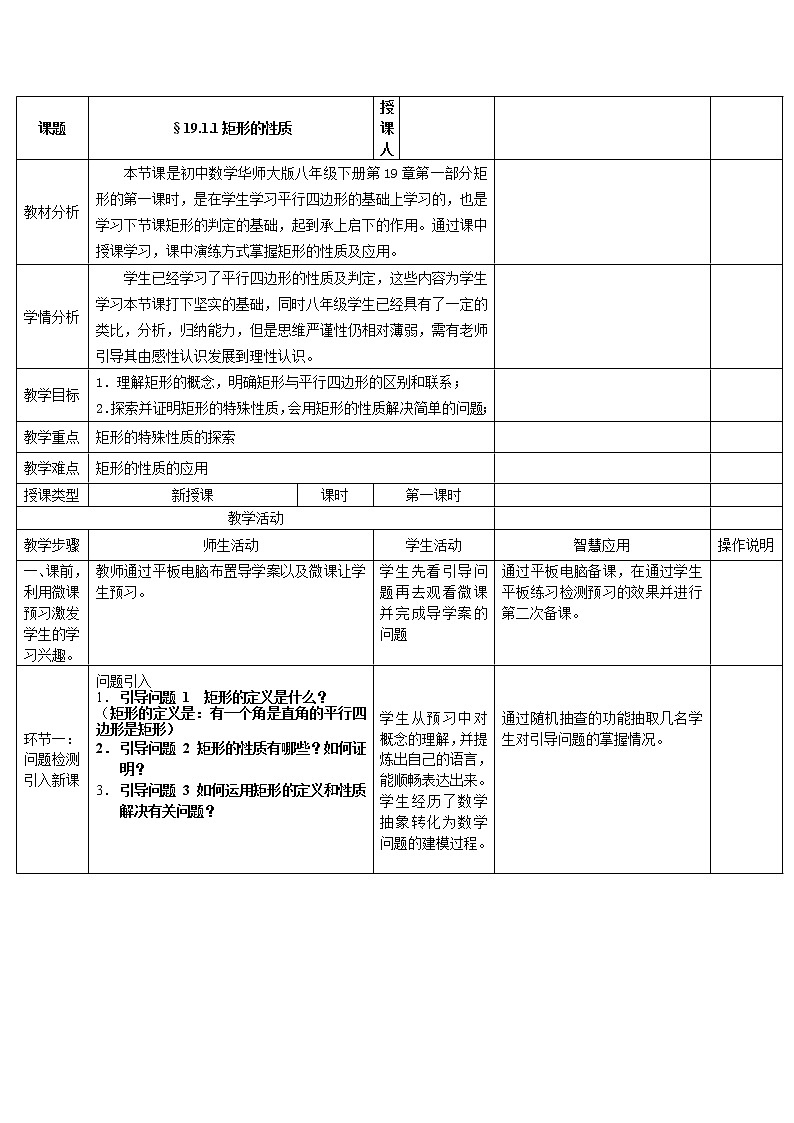
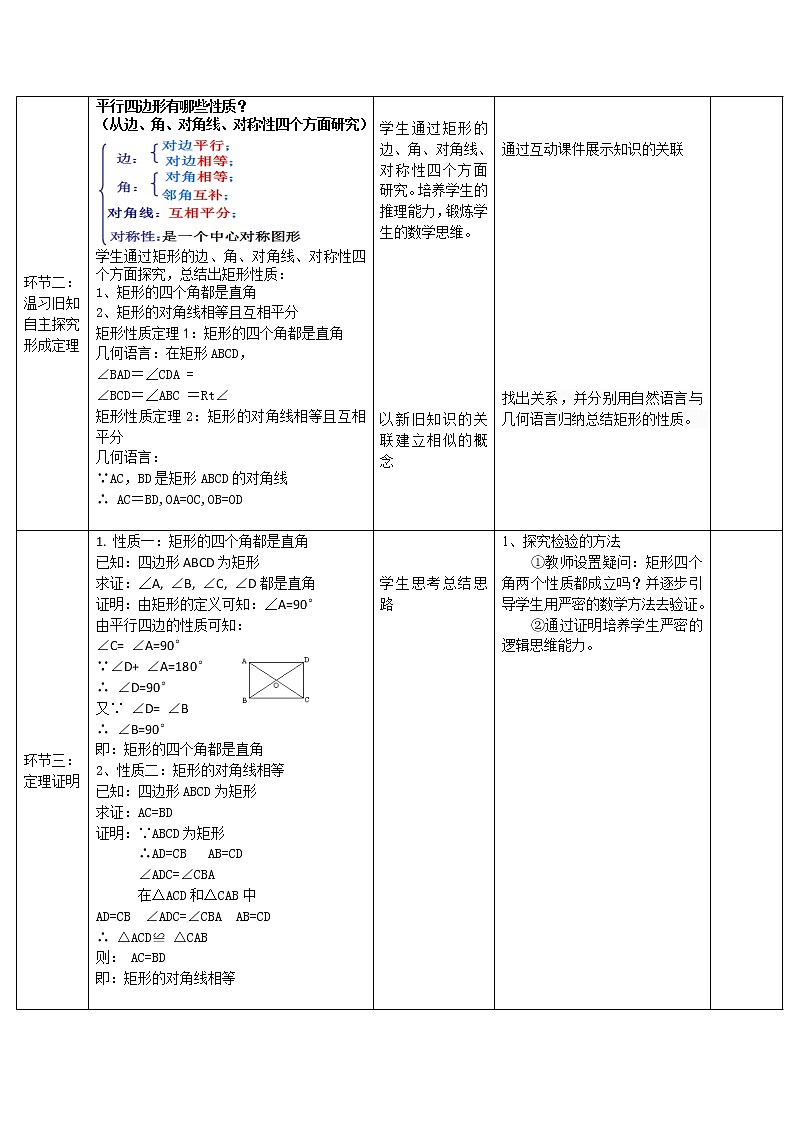
课题§19.1.1矩形的性质授课人   教材分析本节课是初中数学华师大版八年级下册第19章第一部分矩形的第一课时，是在学生学习平行四边形的基础上学习的，也是学习下节课矩形的判定的基础，起到承上启下的作用。通过课中授课学习，课中演练方式掌握矩形的性质及应用。  学情分析学生已经学习了平行四边形的性质及判定，这些内容为学生学习本节课打下坚实的基础，同时八年级学生已经具有了一定的类比，分析，归纳能力，但是思维严谨性仍相对薄弱，需有老师引导其由感性认识发展到理性认识。  教学目标1．理解矩形的概念，明确矩形与平行四边形的区别和联系；2．探索并证明矩形的特殊性质，会用矩形的性质解决简单的问题；  教学重点矩形的特殊性质的探索  教学难点矩形的性质的应用  授课类型新授课课时第一课时  教学活动  教学步骤师生活动学生活动智慧应用操作说明一、课前，利用微课预习激发学生的学习兴趣。教师通过平板电脑布置导学案以及微课让学生预习。学生先看引导问题再去观看微课并完成导学案的问题 通过平板电脑备课，在通过学生平板练习检测预习的效果并进行第二次备课。 环节一：问题检测引入新课 问题引入1．   引导问题 1  矩形的定义是什么？（矩形的定义是：有一个角是直角的平行四边形是矩形）2．   引导问题 2 矩形的性质有哪些？如何证明？3．   引导问题 3 如何运用矩形的定义和性质解决有关问题？  学生从预习中对概念的理解，并提炼出自己的语言，能顺畅表达出来。学生经历了数学抽象转化为数学问题的建模过程。   通过随机抽查的功能抽取几名学生对引导问题的掌握情况。 环节二：温习旧知自主探究形成定理平行四边形有哪些性质？（从边、角、对角线、对称性四个方面研究）学生通过矩形的边、角、对角线、对称性四个方面探究，总结出矩形性质：1、矩形的四个角都是直角2、矩形的对角线相等且互相平分矩形性质定理1：矩形的四个角都是直角几何语言：在矩形ABCD，∠BAD＝∠CDA =∠BCD＝∠ABC ＝Rt∠矩形性质定理2：矩形的对角线相等且互相平分几何语言：∵AC，BD是矩形ABCD的对角线∴ AC＝BD,OA=OC,OB=OD  学生通过矩形的边、角、对角线、对称性四个方面研究。培养学生的推理能力，锻炼学生的数学思维。        以新旧知识的关联建立相似的概念  通过互动课件展示知识的关联           找出关系，并分别用自然语言与几何语言归纳总结矩形的性质。　　 环节三：定理证明1. 性质一：矩形的四个角都是直角已知：四边形ABCD为矩形求证：∠A, ∠B, ∠C, ∠D都是直角证明：由矩形的定义可知：∠A=90°由平行四边的性质可知： ∠C= ∠A=90°∵∠D+ ∠A=180°∴ ∠D=90°又∵ ∠D= ∠B∴ ∠B=90°即：矩形的四个角都是直角2、性质二：矩形的对角线相等已知：四边形ABCD为矩形求证：AC=BD证明：∵ABCD为矩形      ∴AD=CB   AB=CD      ∠ADC=∠CBA      在△ACD和△CAB中AD=CB  ∠ADC=∠CBA  AB=CD∴ △ACD≌ △CAB则： AC=BD即：矩形的对角线相等   学生思考总结思路1、探究检验的方法　　①教师设置疑问：矩形四个角两个性质都成立吗？并逐步引导学生用严密的数学方法去验证。　　②通过证明培养学生严密的逻辑思维能力。 环节四：趁热打铁学以致用一、（1）矩形具有而平行四边形不具有的性质（       ）（A）内角和是360度  （B）对角相等（C）对边平行且相等 （D）对角线相等 （2）下面性质中，矩形不一定具有的是（       ）（A）对角线相等     （B）四个角相等（C）是轴对称图形 （D）对角线垂直（3） 已知矩形的一条对角线与一边的夹角是40°，则两条对角线所夹锐角的度数为       （     ）（A）50° （B）60° （C）70° （D）80°二、1.在矩形ABCD中，AE⊥BD于E，若BE=OE=1，则AC=     , AB=     ,  2、如图，在矩形ABCD中，矩形ABCD的对角线AC、BD相交于点O,AC=4cm,∠AOB=60°，则AB=    cm.          学生通过平板完成练习       矩形问题可以转化成等边三角形或直角三角形的问题去解决。           方法：如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形。 深化矩形概念：教师发送一套互动试题，检测学生对矩形概念的认识。结束练习后，根据平台的自动批改与统计结果，教师可以进行针对性的讲解，并预知学生对新知识已有认知的水平，为更高效地讲授新知打下基础。     通过互动题板/随机对比/学生互评/问答题/拍照上传
　　1、定义反馈
　　①教师发送互动题板：给出矩形概念以及性质的题检测学生对矩形定义、性质的掌握情况。

　　②学生答题结束后，进行学生间相互评价（星级表示），学生可以看到其他同伴对自己的评价；
　　③教师随机对比4个同学的答案，进行点评，实现课堂评价的多元化与公平性。④教师发送一道针对矩形性质应用的问答题，学生在纸上作答并拍照上传，完成作答后对其他同学上传的答案进行评价。
　　⑤通过随机抽取选择两位同学的答案进行针对性讲解与点评，让学生进一步掌握运用矩形的性质解决数学问题的方法           环节五：例题讲解例1：矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形周长的和为86cm，对角线长为13cm，那么矩形的周长是多少？解：∵ △AOB、△BOC、△COD和△AOD四个小三角形的周长和为86cm ∴ AB+BC+CD+DA+2(OA+OB+OC+OD) = AB+BC+CD+DA+2(AC+BD) = 86 又∵ AC=BD=13 ∴AB+BC+CD+DA=86-2（AC+BD）= 86-4×13=34（cm）即矩形的周长是34cm 矩形问题可以转化成等边三角形或直角三角形的问题去解决。 通过同屏、广播、直播功能讲解例题，让学生更加直观的对问题解决思路的掌握。 环节六：开放训练体现应用快乐练习：1.如图，矩形ABCD的两条对角线交于点O，且∠AOD＝120°，你能说AC＝2AB吗？                                   如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形①教师发送一道针对矩形性质应用的问答题，学生在纸上作答并拍照上传，完成作答后对其他同学上传的答案进行评价。
　　②通过随机抽取选择两位同学的答案进行针对性讲解与点评，让学生进一步掌握运用矩形的性质解决数学问题的方法
　　 环节七：课堂小结 通过本节课，你学到了什么？学生独立总结通过同屏展示网络格式的总结，让学生对知识点掌握更加的直观 环节八：布置作业   通过平台发送作业