






人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系完美版课件ppt
展开
这是一份人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系完美版课件ppt,共34页。PPT课件主要包含了平面的基本性质及作用,三个基本事实,三个推论,l在α内,l在α外,lm相交于A,lα相交于A,αβ相交于l,l⊄α,l⊂α等内容,欢迎下载使用。
Ping mian
我们已经认识了柱体、锥体、台体等多面体,它们都是由点、线、面构成的,同时,还知道了多面体的一些结构特征,为了进一步研究立体图形的有关问题,需要对点、线、面以及它们之间的位置关系进行再研究。
在初中平面几何中,我们对点和直线有了一定的认识,知道它们都是由现实事物抽象得到的。生活中也有一些物体给我们以平面的直观感觉,比如:桌面、黑板面、平静的水面等.
几何里所说的“平面”就是从这样的一些物体中抽象出来的.类似于直线向两端无限延伸。
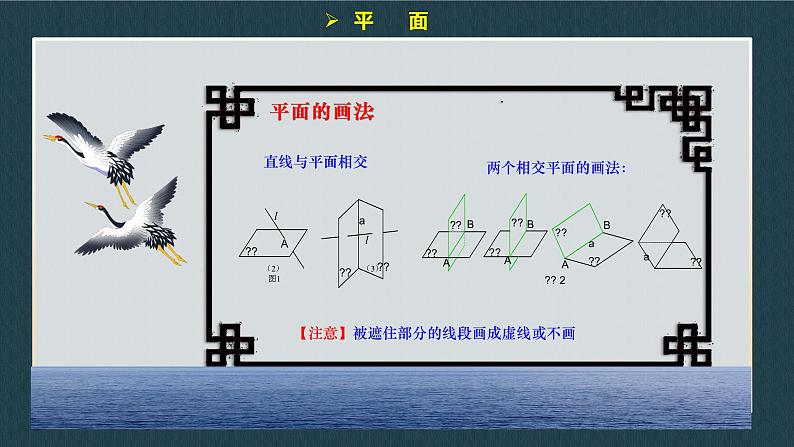
如图所示,与画出直线的一部分表示直线一样,我们可以画出平面的一部分来表示平面. 通常用平行四边形表示平面.
当平面水平放置时,常把平行四边形的一边画成横向;
当平面竖直放置时,常把平行四边形的一边画成竖向.
【注意】被遮住部分的线段画成虚线或不画
图①的平面可表示为平面α、平面AC、平面BD、平面ABCD等
Pingmiandejibenxingzhijizuyng
【问题】 同学们知道:两点可以确定一条直线,那么几点可以确定一个平面呢?
基本事实1 :不在一条直线上的三个点,有且只有一个平面.
简记为:不共线的三点确定一个平面(确定平面的条件).
直线上有无数个点, 平面内有无数个点, 直线、平面都可以看成是点的集合.
点A在直线l上, 记作A∈l; 点B在直线l外, 记作B∉l.
点A在平面α内,记作A∈α; 点P在平面α外,记作P∉α.
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
【经验】在实际生活中,我们有这样的经验,如果一根直尺边缘上的任意两点在桌面上,那么 直尺的整个边缘就落在了桌面上,上述经验和类似的事实可以归纳为以下基本事实:
平面内有无数条直线, 平面可以看成是直线的集合.
如果直线l上所有点都在平面α内,就说直线l在平面α内,记作l⊂α;
如果直线l上有一点不在平面α内,就说直线l不在平面α内,记作l ⊄α.
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该 点的公共直线.
若平面α与β相交于直线l,则把l叫做α与β的交线,记作α∩β=l .
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
利用基本事实1和基本事实2,再结合“两点确定一条直线”,可以得到下面三个推论:
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
点、直线、平面之间的基本位置关系及语言表达
Dianzhixianpingmianzhijiandejibenweizhiguanxijiyuyanbiada
例1. 判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”. (1) 书桌面是平面.( ) (2) 平面α与平面β相交,它们只有有限个公共点.( ) (3) 如果两个平面有三个不共线的公共点,那么这两个平面重合.( )
变式:判断正误. (1) 平面是处处平的面.( ) (2) 平面是无限延展的.( ) (3) 平面的形状是平行四边形.( ) (4) 一个平面的厚度可以是0.001 cm.( )
下列命题正确的是( ). (A) 三点确定一个平面. (B) 一条直线和一个点确定一个平面. (C) 圆心和圆上两点可确定一个平面. (D) 梯形可确定一个平面.
例3. 不共面的四点可以确定几个平面?
例4. 用符号表示下列语句,并画出相应的图形. (1) 点A在平面α内,点B在平面α外. (2) 直线a既在平面α内,又在平面β内.
解 (1) A∈α,A∉β.(如图①)
(2)A∈a,B∈a,A∈α,B∉α,a⊄α.(如图②)
(3)α∩β=a.(如图③)
解(1) 直线和平面都是由点组成的集合,所以A∈b,b⊂β.
(2) 由题图知α∩β=m,n⊂α且m∩n=A,A∈m,A∈n.
例6 求证:两两相交且不共点的三条直线在同一平面内.
如图, l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.
证明 方法一 (纳入法) ∵l1∩l2=A,∴l1和l2确定一个平面α. ∵l2∩l3=B,∴B∈l2. 又∵l2⊂α,∴B∈α. 同理可证C∈α. ∵B∈l3,C∈l3,∴l3⊂α. ∴直线l1,l2,l3在同一平面内.
方法二 (同一法)∵l1∩l2=A,∴l1和l2确定一个平面α.∵l2∩l3=B,∴l2和l3确定一个平面β.∵A∈l2,l2⊂α,∴A∈α.∵A∈l2,l2⊂β,∴A∈β.同理可证B∈α,B∈β,C∈α,C∈β.∴不共线的三个点A,B,C既在平面α内,又在平面β内,∴平面α和β重合,即直线l1,l2,l3在同一平面内.
例7 已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面.
证明 如图所示,∵a∥b, ∴过a,b有且只有一个平面α. 设a∩l=A,b∩l=B, ∴A∈α,B∈α,且A∈l,B∈l, ∴l⊂α,即过a,b,l有且只有一个平面.
证: 如图,∵在梯形ABCD中AD∥BC,∴AB与CD必交于一点,
设AB交CD于点M,则M∈AB,M∈CD,
又∵AB⊂α,CD⊂β,∴M∈α,M∈β,
又∵α∩β=l, ∴M∈l, ∴AB,CD,l共点.
证: ∵AB∥CD,∴AB,CD确定一个平面β, ∵AB∩α=E,E∈AB,E∈α,∴E∈β, ∴E在α与β的交线l上. 同理,F,G,H也在α与β的交线l上, ∴E,F,G,H四点必定共线.
1.知识点: (1)平面的概念. (2)点、线、面之间的位置关系. (3)平面的基本性质及作用.
2.方法:同一法、纳入法.
3.易错点:三种语言的相互转换.
1.下列图形中不一定是平面图形的是A.三角形B.菱形C.梯形D.四边相等的四边形
2.(多选)下列说法不正确的是 A.三点可以确定一个平面 B.空间中两条直线能确定一个平面 C.共点的三条直线确定一个平面 D.圆和平行四边形都可以表示一个平面
解 不共线的三点有且仅有一个平面,故A错误; 只有平行或相交的直线才能确定一个平面,故B错误; 当三条直线相交于一点时,可以确定三个平面,例如三棱锥的三条侧棱,故C错误; 圆和平行四边形是平面图形,可以用来表示平面,故D正确.
3.若直线l与平面α相交于点O,A,B∈l,C,D∈α, 且AC∥BD, 求证:O,C,D三点共线.
证 如图,∵AC∥BD, ∴AC与BD确定一个平面,记作平面β, 则α∩β=直线CD. ∵l∩α=O,∴O∈α. 又∵O∈AB,AB⊂β, ∴O∈β, ∴O∈直线CD,∴O,C,D三点共线.
4.如图,设不全等的△ABC与△A1B1C1不在同一个平面内, 且AB∥A1B1,BC∥B1C1,CA∥C1A1,求证:AA1,BB1, CC1三线共点.
证:不妨设AB≠A1B1,则四边形AA1B1B为梯形, ∴AA1与BB1相交,设其交点为S, 则S∈AA1,S∈BB1. ∵BB1⊂平面BCC1B1,∴S∈平面BCC1B1. 同理可证,S∈平面ACC1A1, ∴点S在平面BCC1B1与平面ACC1A1的交线上,即S∈CC1, ∴AA1,BB1,CC1三线共点.
相关课件
这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教案配套课件ppt,共33页。PPT课件主要包含了学习目标,新知学习,知识点一平面,三个推论,易错辨析,典例剖析,线共面,随堂小测,课堂小结等内容,欢迎下载使用。
这是一份人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系完美版课件ppt,共33页。PPT课件主要包含了学习目标,新知学习,易错辨析,典例剖析,随堂小测,课堂小结等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系授课ppt课件,共41页。










