专题05 四边形的综合问题 -备战2022年中考数学复习重难点与压轴题型专项训练

这是一份专题05 四边形的综合问题 -备战2022年中考数学复习重难点与压轴题型专项训练，文件包含专题05四边形的综合问题解析版-备战2022年中考数学复习重难点与压轴题型专项训练docx、专题05四边形的综合问题原卷版-备战2022年中考数学复习重难点与压轴题型专项训练docx等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。
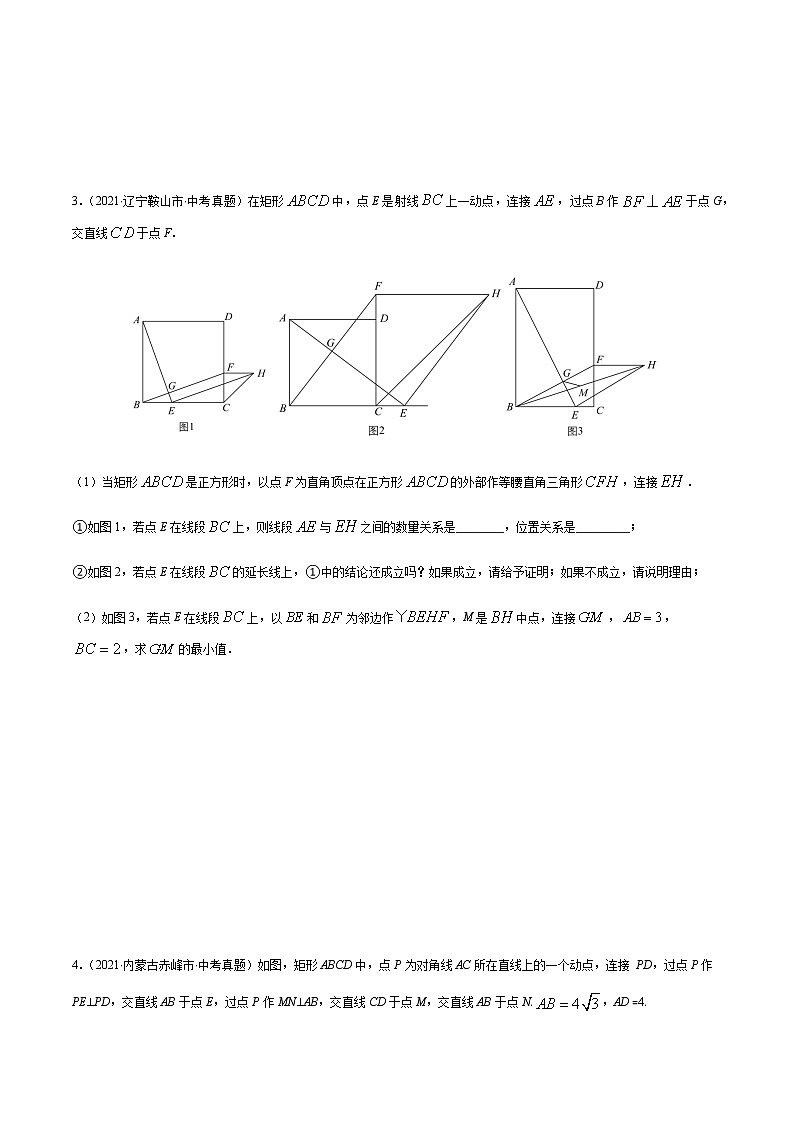
备战2022年中考复习重难点与压轴题型专项训练专题05 四边形的综合问题【专题训练】一、解答题1．（2021·广西贵港市·中考真题）已知：在矩形ABCD中，AB=6，，P是BC边上的一个动点，将矩形ABCD折叠，使点A与点P重合，点D落在点G处，折痕为EF．（1）如图1，当点P与点C重合时，则线段EB=_______________，EF=_____________；（2）如图2，当点P与点B，C均不重合时，取EF的中点O，连接并延长PO与GF的延长线交于点M，连接PF，ME，MA．①求证：四边形MEPF是平行四边形：②当时，求四边形MEPF的面积．       2．（2021·山东青岛市·中考真题）已知：如图，在四边形和中，，，点在上，，，，延长交于点，点从点出发，沿方向匀速运动，速度为；同时，点从点出发，沿方向匀速运动，速度为，过点作于点，交于点．设运动时间为．解答下列问题：     （1）当为何值时，点在线段的垂直平分线上？（2）连接，作于点，当四边形为矩形时，求的值；（3）连接，，设四边形的面积为，求与的函数关系式；（4）点在运动过程中，是否存在某一时刻，使点在的平分线上？若存在，求出的值；若不存在，请说明理由．         3．（2021·辽宁鞍山市·中考真题）在矩形中，点E是射线上一动点，连接，过点B作于点G，交直线于点F．（1）当矩形是正方形时，以点F为直角顶点在正方形的外部作等腰直角三角形，连接．①如图1，若点E在线段上，则线段与之间的数量关系是________，位置关系是_________；②如图2，若点E在线段的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；（2）如图3，若点E在线段上，以和为邻边作，M是中点，连接，，，求的最小值．      4．（2021·内蒙古赤峰市·中考真题）如图，矩形ABCD中，点P为对角线AC所在直线上的一个动点，连接 PD，过点P作PE⊥PD，交直线AB于点E，过点P作MN⊥AB，交直线CD于点M，交直线AB于点N.，AD =4.（1）如图1，①当点P在线段AC上时，∠PDM和∠EPN的数关系为:∠PDM___ ∠EPN；②的值是            ；（2）如图2，当点P在CA延长线上时，（1）中的结论②是否成立?若成立，请证明；若不成立，说明理由；（3）如图3，以线段PD ，PE为邻边作矩形PEFD.设PM的长为x，矩形PEFD的面积为y.请直接写出y与x之间的函数关系式及y的最小值.     5．（2021·湖南益阳市·中考真题）定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形，根据以上定义，解决下列问题：（1）如图1，正方形中，是上的点，将绕点旋转，使与重合，此时点的对应点在的延长线上，则四边形为“直等补”四边形，为什么？（2）如图2，已知四边形是“直等补”四边形，，，，点到直线的距离为．①求的长．②若、分别是、边上的动点，求周长的最小值．         6．（2021·吉林中考真题）能够完全重合的平行四边形纸片和按图①方式摆放，其中，．点，分别在边，上，与相交于点．（探究）求证：四边形是菱形．（操作一）固定图①中的平行四边形纸片，将平行四边形纸片绕着点顺时针旋转一定的角度，使点与点重合，如图②，则这两张平行四边形纸片未重叠部分图形的周长和为______．（操作二）四边形纸片绕着点继续顺时针旋转一定的角度，使点与点重合，连接，，如图③若，则四边形的面积为______．       7．（2021·广东深圳市·中考真题）背景：一次小组合作探究课上，小明将两个正方形按背景图位置摆放（点E，A，D在同一条直线上），发现BE=DG且BE⊥DG．小组讨论后，提出了三个问题，请你帮助解答：（1）将正方形AEFG绕点A按逆时针方向旋转，（如图1）还能得到BE=DG吗？如果能，请给出证明．如若不能，请说明理由：（2）把背景中的正方形分别改为菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转，（如图2）试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE=DG仍成立？请说明理由；（3）把背景中的正方形改成矩形AEFG和矩形ABCD，且，AE=4，AB=8，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG．小组发现：在旋转过程中， BG2+DE2是定值，请求出这个定值．     8．（2021·山西中考真题）综合与实践问题情境：如图①，点为正方形内一点，，将绕点按顺时针方向旋转，得到（点的对应点为点），延长交于点，连接．猜想证明：（1）试判断四边形的形状，并说明理由；（2）如图②，若，请猜想线段与的数量关系并加以证明；解决问题：（3）如图①，若，，请直接写出的长．          9．（2021·湖南邵阳市·中考真题）已知：如图①，将一块45°角的直角三角板与正方形的一角重合，连接，点M是的中点，连接．（1）请你猜想与的数量关系是__________．（2）如图②，把正方形绕着点D顺时针旋转角（）．①与的数量关系是否仍成立，若成立，请证明；若不成立，请说明理由；（温馨提示：延长到点N，使，连接）②求证：；③若旋转角，且，求的值．（可不写过程，直接写出结果）      10．（2021·湖北宜昌市·中考真题）菱形的对角线相交于点O，，点G是射线上一个动点，过点G作交射线于点E，以为邻边作矩形．（1）如图1，当点F在线段上时，求证：；（2）若延长与边交于点H，将沿直线翻折180°得到．①如图2，当点M在上时，求证：四边形为正方形：②如图3，当为定值时，设，k为大于0的常数，当且仅当时，点M在矩形的外部，求m的值．             11．（2021·湖南岳阳市·中考真题）如图1，在矩形中，，动点，分别从点，点同时以每秒1个单位长度的速度出发，且分别在边上沿，的方向运动，当点运动到点时，两点同时停止运动，设点运动的时间为，连接，过点作，与边相交于点，连接．（1）如图2，当时，延长交边于点．求证：；（2）在（1）的条件下，试探究线段三者之间的等量关系，并加以证明；（3）如图3，当时，延长交边于点，连接，若平分，求的值．      12．（2021·四川成都市·中考真题）在矩形的边上取一点，将沿翻折，使点恰好落在边上点处．（1）如图1，若，求的度数；（2）如图2，当，且时，求的长；（3）如图3，延长，与的角平分线交于点，交于点，当时，求出的值．        13．（2021·贵州贵阳市·中考真题）如图，四边形是正方形，点为对角线的中点．（1）问题解决：如图①，连接，分别取，的中点，，连接，则与的数量关系是_____，位置关系是____；（2）问题探究：如图②，是将图①中的绕点按顺时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．判断的形状，并证明你的结论；（3）拓展延伸：如图③，是将图①中的绕点按逆时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．若正方形的边长为1，求的面积．      14．（2021·辽宁丹东市·中考真题）已知：菱形和菱形，，起始位置点在边上，点在所在直线上，点在点的右侧，点在点的右侧，连接和，将菱形以为旋转中心逆时针旋转角（）．（1）如图1，若点与重合，且，求证：；（2）若点与不重合，是上一点，当时，连接和，和所在直线相交于点；①如图2，当时，请猜想线段和线段的数量关系及的度数；②如图3，当时，请求出线段和线段的数量关系及的度数；③在②的条件下，若点与的中点重合，，，在整个旋转过程中，当点与点重合时，请直接写出线段的长．