


初中数学沪教版 (五四制)八年级下册第二十一章 代数方程综合与测试同步达标检测题
展开
第21章 代数方程(巩固篇)
姓名:___________考号:___________分数:___________
(考试时间:100分钟 满分:120分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.桌面上有甲、乙、丙三个圆柱形的杯子,杯深均为15公分,各装有10公分高的水,且表记录了甲、乙、丙三个杯子的底面积.今小明将甲、乙两杯内一些水倒入丙杯,过程中水没溢出,使得甲、乙、丙三杯内水的高度比变为3:4:5.若不计杯子厚度,则甲杯内水的高度变为多少公分?( )
| 底面积(平方公分) |
甲杯 | 60 |
乙杯 | 80 |
丙杯 | 100 |
A.5.4 B.5.7 C.7.2 D.7.5
【答案】C
【解析】
试题解析:设后来甲、乙、丙三杯内水的高度为
根据题意得:
解得:x=2.4,
则甲杯内水的高度变为3×2.4=7.2(厘米).
故选C.
2.某幼儿园要准备修建一个面积为210平方米的矩形活动场地,它的长比宽多12米,设场地的长为x米,可列方程为
A. B.
C. D.
【答案】B
【解析】
设场地的长为x米,则宽为(x﹣12)米,根据面积可列方程,
x(x﹣12)=210,
故选B.
3.从一块正方形铁皮的四角上各剪去一个边长为3cm的小正方形,制成一个无盖的盒子,若盒子的容积为300cm3,则铁皮的边长为( )
A.16cm B.14cm C.13cm D.11cm
【答案】A
【解析】
试题分析:正方形铁皮的边长应是x厘米,则没有盖的长方体盒子的长、宽为(x-3×2)厘米,高为3厘米,根据题意列方程得,(x-3×2)(x-3×2)×3=300,解得=16,=-4(不合题意,舍去);答:正方形铁皮的边长应是16cm.故选A.
4.购买一本书,打八折比打九折少花2元钱,那么这本书的原价是( )
A.10 B.15 C.20 D.25
【答案】C
【解析】解:设原价为x元,由题意得:0.9x-0.8x=2
解得:x=20.故选C.
5.年月日,北京市正式实施《北京市生活垃圾管理条例》,生活垃圾按照厨余垃圾,可回收物,有害垃圾,其他垃圾进行分类.小红所住小区月和月的厨余垃圾分出量和其他三种垃圾的总量的相关信息如下表所示:
类别 月份 | 月 | 月 |
厨余垃圾分出量(千克) | ||
其他三种垃圾的总量(千克) |
厨余垃圾分出量如果厨余垃圾分出率(生活垃圾总量厨余垃圾分出量其他三种垃圾的总量),且该小区月的厨余垃圾分出率约是月的厨余垃圾分出率的倍,那么下面列式正确的是( )
A. B.
C. D.
【答案】B
5月份厨余垃圾分出率=,12月份厨余垃圾分出率= ,
∴由题意得,
故选:B.
6.某工程需要在规定时间内完成,如果甲工程队单独做,恰好如期完成; 如果乙工程队单独做,则多用天,现在甲、乙两队合做天,剩下的由乙队单独做,恰好如期完成,求规定时间.如果设规定日期为天,下面所列方程中错误的是( )
A. B. C. D.
【答案】D
解:设规定日期为天,
由题意可得,,
整理得,或或.
则选项均正确,
故选:D.
7.一辆拖拉机以每小时36千米的速度在公路上行驶,开向寂静的山谷,驾驶员按一声喇叭,3秒后听到回响,这时拖拉机离山谷的距离是( )米.(声音的速度是340米/秒)
A.495 B.490 C.525 D.510
【答案】A
解:如图:
36千米/小时=10米/秒.
设这时拖拉机离山谷的距离是x米,
依题意,得:340×310×3=2x,
解得:x=495.
故选:A.
8.分式方程的解为( )
A. B. C. D.
【答案】A
解:去分母,方程两边同时乘以,
得:,
,
,
检验:时,,
∴原方程的解是
故选A.
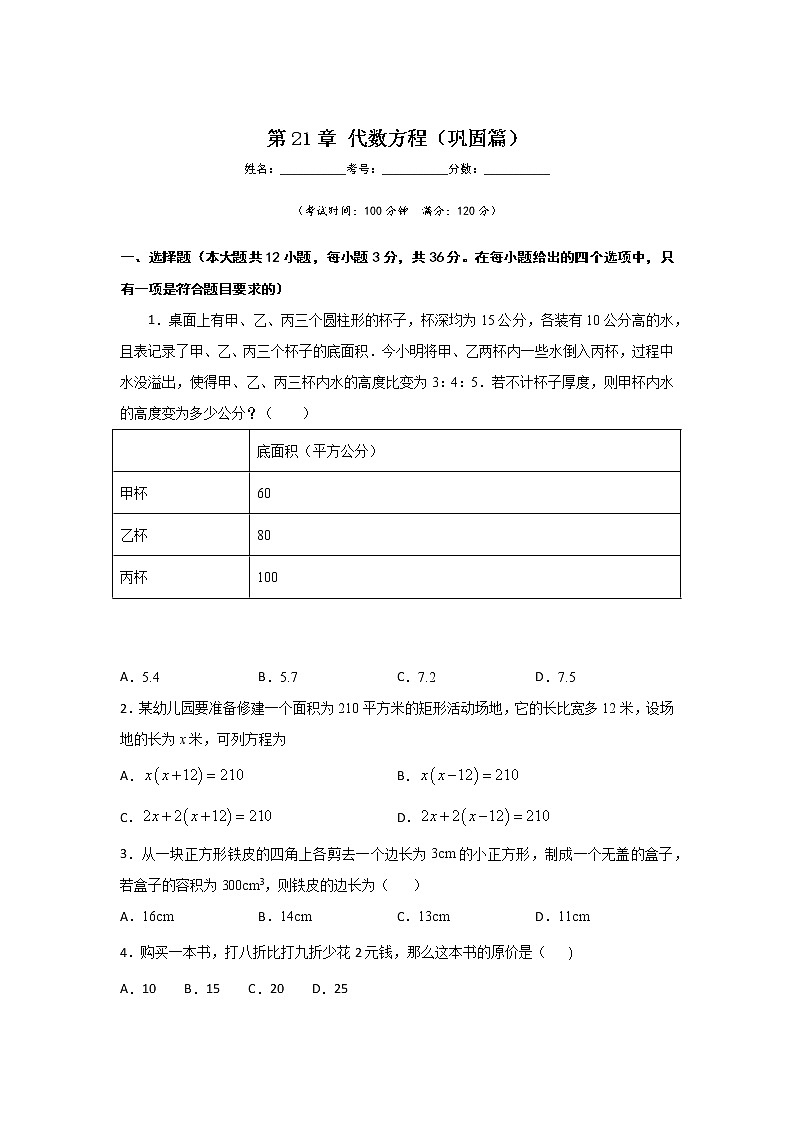
9.图中以两直线,的交点坐标为解的方程组是( )
A. B.
C. D.
【答案】B
解:设一次函数的解析式为:.
①直线经过、,
,
解得,,
函数解析式为,即;
②直线经过、,
,
解得,,
函数解析式为,即;
因此以两条直线,的交点坐标为解的方程组是:.
故选:B.
10.对于两个不相等的有理数a,b,我们规定符号max{a,b}表示a,b两数中较大的数,例如max{2,4}=4.按照这个规定,那么方程max{x,-x}=3x-2的解为( )
A. B.1 C.1或 D.或
【答案】B
解:当x>-x,即x>0时,方程变形得:x=3x-2,
解得:x=1;
当x<-x,即x<0时,方程变形得:-x=3x-2,
解得:x=,不符合题意;
∴方程max{x,-x}=3x-2的解为1,
故选:B.
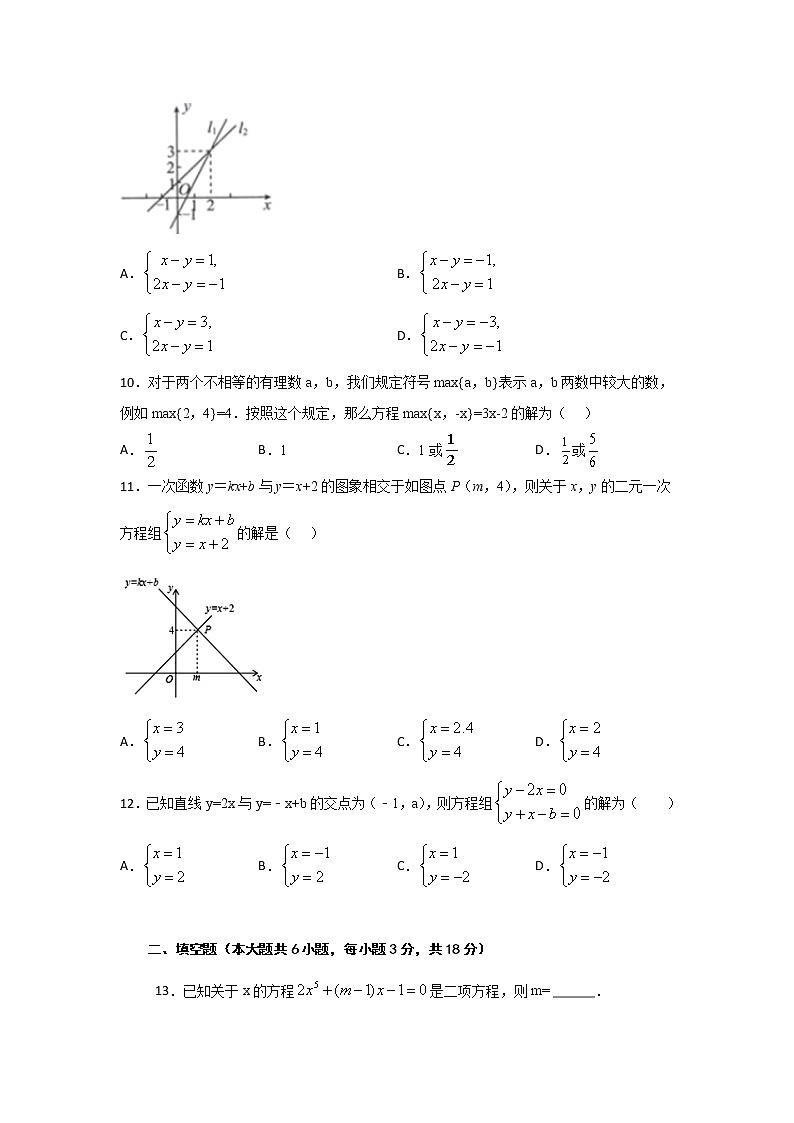
11.一次函数y=kx+b与y=x+2的图象相交于如图点P(m,4),则关于x,y的二元一次方程组的解是( )
A. B. C. D.
【答案】D
解:把P(m,4)代入y=x+2得m+2=4,解得m=2,
所以P点坐标为(2,4),
所以关于x,y的二元一次方程组的解是
故答案选:D.
12.已知直线y=2x与y=﹣x+b的交点为(﹣1,a),则方程组的解为( )
A. B. C. D.
【答案】D
将点(,)代入可得:,
∴直线与直线的交点为(,),
而方程组可变形为:,
∴原方程组的解为:,
故选:D.
二、填空题(本大题共6小题,每小题3分,共18分)
13.已知关于x的方程是二项方程,则m= ______.
【答案】1
解:∵关于x的方程是二项方程,
∴,即,
故答案为:1.
14.已知直线和y=-3x,则它们的交点的坐标为___________.
【答案】(-1,3).
解:解二元一次方程组得:
∴两条直线的交点坐标为:(-1,3).
故答案为:(-1,3).
15.分式方程的解为______.
【答案】x=-2
解:去分母得:x(x+1)+1=(x+1)(x﹣1),
去括号,得:x2+x+1=x2﹣1,
移项、合并同类项,得:x=﹣2,
检验得(x+1)(x﹣1)=3≠0,
所以方程的解为:x=﹣2,
故答案为:x=﹣2.
16.方程的根是____.
【答案】.
解:,
,
,
,
经检验是原方程的根,
.
故答案为:.
17.小亮利用8个同样大小的长方形小木块拼成下面两个图形,经测量得知图②中的小正方形(阴影部分)的面积为,则一个长方形小木块的周长为________.
【答案】16
解:设这8个大小一样的小长方形的长为,宽为.
由题意,得,
解得.
小长方形的周长为,
故答案为.
18.某种商品的标价为元,若以九折降价出售,仍可获利,设该商品的进货价为元,可列方程为_____________________.
【答案】.
解:设进货价为元,
由题意得,,
故答案为:.
三、解答题 (本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程)
19.在平面直角坐标系xOy中,一次函数y=kx+b的图象与直线y=3x平行,且经过点A(1,6).
(1)求一次函数y=kx+b的解析式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
【答案】(1)y=3x+3;(2)
解:(1)∵函数y=kx+b的图象与直线y=3x平行,
∴k=3,
又∵函数y=3x+b的图象经过点A(1,6),
∴6=3+b,
解得b=3,
∴一次函数的解析式为y=3x+3;
(2)在y=3x+3中,令x=0,则y=3;令y=0,则x=﹣1;
∴一次函数y=kx+b的图象与坐标轴交于(0,3)和(﹣1,0),
∴一次函数y=kx+b的图象与坐标轴围成的三角形的面积为 ×1×3=.
20.解下列方程:
(1);
(2);
(3);
(4).
【答案】(1);(2);(3);(4)无解.
(1)去分母,可得,解得,
经检验是分式方程的解,
所以方程的解为;
(2)去分母,可得,解得,
经检验是分式方程的解,
所以方程的解为.
(3),即,即,
即,解得,
经检验,是原方程的根.
(4),去分母得,
化简得,解得,
经检验为方程的增根,原方程无解.
21.解方程组:
【答案】,.
解:设=m,=n,则x=m2-1,y=n2+2,
原方程组可化为
把m+n=5看作①,把看作②,
由①,得m =5-n③
③代入②,得(5-n)2+n2=13,
整理,得2n2-10n+12=0,
即n2-5n+6=0,
解这个方程,得n =2或3,
∴
∴原方程组的解为.
22.解分式方程
(1)
(2)
【答案】(1); (2)
解:(1)
去分母得,3-2=3(2x-2)
去括号得,1=6x-6
移项,合并同类项,得:7=6x
系数化为1,得:
检验:当时,2x-2=≠0
则方程的解为;
(2)
去分母得,
整理得:4x=12
解得,x=3
经检验,x=3是原方程的解,
23.观察下列式子,探索它们的规律并解决问题
…
(1)用正整数表示这个规律:=_________,
试着推论:=______,=_______
_________,
(2)用(1)中的结论计算:
(3)用(1)中的结论解下列方程:
【答案】(1); ;;;
(2) ;(3)4038
解:(1)=
=
=
=
(2)
===
=
=
=
(3)
利用(1)的结论,原方程变形为:
解方程,得:x=4038
检验:当x=4038时,2x(x+2019)≠0
∴x=4038是原分式方程的解.
24.某电厂规定,该厂家属区每户居民如果一个月的用电量不超过A 千瓦·时,那么这户居民这个月只需交10元电费;如果超过A 千瓦·时,则这个月除了要交10元的用电费以外,超过的部,分还要按每千瓦·时 元交费.
(1)该厂某居民2月份用电90千瓦·时,超过了规定的 A 千瓦·时,则超过的部分应交电费 元(用A 表示);
(2)下表是这户居民3月、4月用电情况和交费情况:
月份 | 用电量(千瓦时) | 交电费总数(元) |
3 | 80 | 25 |
4 | 45 | 10 |
根据上表数据,你能求电厂规定的A的值吗? 试试看.
【答案】(1);(2)50
【解析】
分析:(1)由于超过部分要按每千瓦时元收费,所以超过部分电费(90−A)•,化简即可;
(2)依题意,得:(80−A)•=15,解方程即可.此外从表格中知道没有超过45时,电费还是10元,由此可以舍去不符合题意的结果.
详解:(1)(90−A)×;
(2)由表中数据可知(80−A)×+10=25,
得 A2−80A+1500=0,
解得 A1=30,A2=50,
又∵用电45千瓦•时,付费总额10元,
∴A>45,
∴A=50
数学沪教版 (五四制)第二十三章 概率初步综合与测试习题: 这是一份数学沪教版 (五四制)第二十三章 概率初步综合与测试习题,文件包含第23章概率初步强化篇解析版doc、第23章概率初步强化篇原卷版doc等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
数学八年级下册第二十三章 概率初步综合与测试课时练习: 这是一份数学八年级下册第二十三章 概率初步综合与测试课时练习,文件包含第23章概率初步巩固篇解析版doc、第23章概率初步巩固篇原卷版doc等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
2021学年第二十二章 四边形综合与测试练习: 这是一份2021学年第二十二章 四边形综合与测试练习,文件包含第22章四边形巩固篇解析版doc、第22章四边形巩固篇原卷版doc等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。













