
所属成套资源:2022中考数学一轮专题复习学案
备考2022中考数学一轮专题复习学案06 一元一次方程
展开
这是一份备考2022中考数学一轮专题复习学案06 一元一次方程,共8页。
中考命题说明
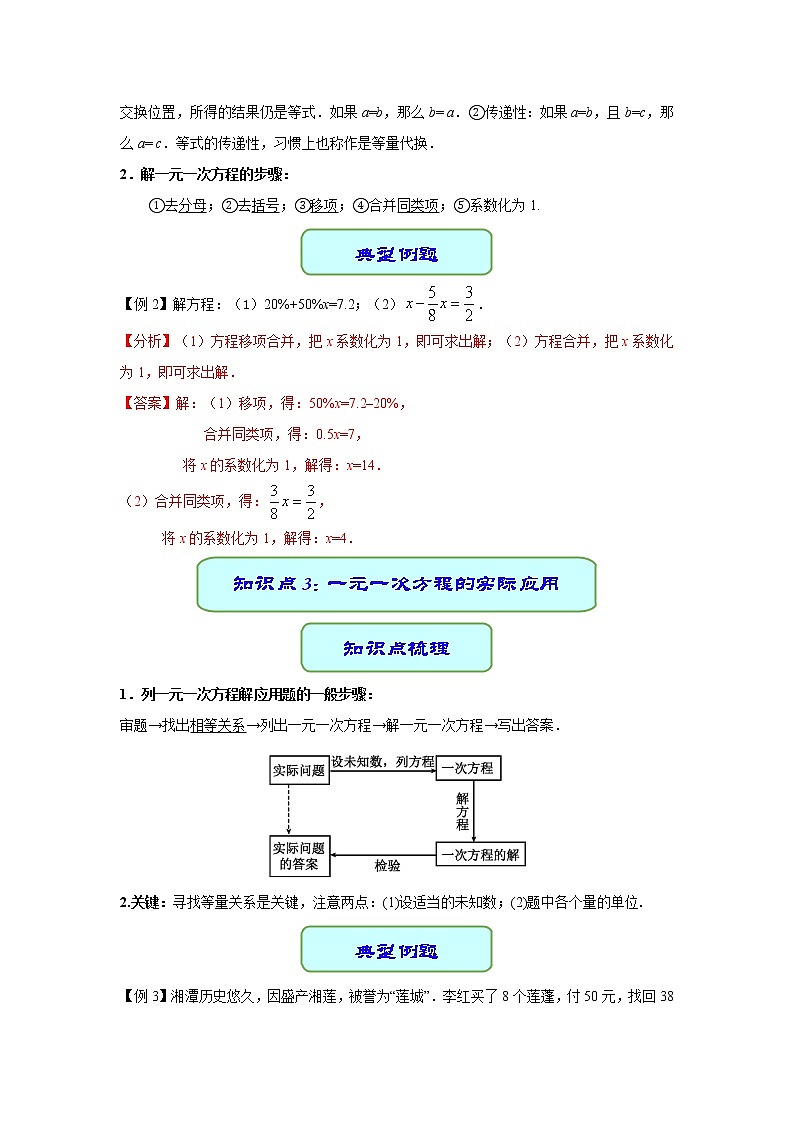
思维导图
知识点1:方程的有关概念
知识点梳理
1.方程、方程的解、解方程:
(1)含有未知数的等式叫做方程.
(2)使方程左右两边的值相等的未知数的值,叫做方程的解.
(3)求方程解的过程叫做解方程.
注意:方程的解与解方程不同.
2.一元一次方程:
在整式方程中,只含有1个未知数,并且未知数的最高次数是1,系数不等于0的方程叫做一元一次方程.
3.一元一次方程的一般形式: ax+b=0(a,b为常数,且a≠0) .
典型例题
【例1】已知3是关于x的方程2x-a=1的解,则a的值是( )
A.-5 B.5 C.7 D.2
【分析】直接利用方程的解的定义可得出关于a的方程:6-a=1,所以a=5.
【答案】B.
知识点2:一元一次方程的解法
知识点梳理
1.等式的基本性质:
(1)等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c= b±c.
(2)等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac= bc;如果a=b(c≠0),那么=.
(3)等式除了以上两条性质外,还有其他的一些性质:①对称性:等式的左、右两边交换位置,所得的结果仍是等式.如果a=b,那么b= a.②传递性:如果a=b,且b=c,那么a= c.等式的传递性,习惯上也称作是等量代换.
2.解一元一次方程的步骤:
①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.
典型例题
【例2】解方程:(1)20%+50%x=7.2;(2).
【分析】(1)方程移项合并,把x系数化为1,即可求出解;(2)方程合并,把x系数化为1,即可求出解.
【答案】解:(1)移项,得:50%x=7.2–20%,
合并同类项,得:0.5x=7,
将x的系数化为1,解得:x=14.
(2)合并同类项,得:,
将x的系数化为1,解得:x=4.
知识点3:一元一次方程的实际应用
知识点梳理
1.列一元一次方程解应用题的一般步骤:
审题→找出相等关系→列出一元一次方程→解一元一次方程→写出答案.
2.关键:寻找等量关系是关键,注意两点:(1)设适当的未知数;(2)题中各个量的单位.
典型例题
【例3】湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个莲蓬,付50元,找回38元,设每个莲蓬的价格为x元,根据题意,列出方程为__________________.
【分析】本题考查二次根式有意义的条件,根据被开方数大于或等于0,列出不等式x-2≥0,解不等式即可.
【答案】50-8x=38.
【例4】根据省“十三五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的2小时18分钟缩短为36分钟,其速度每小时将提高260 km,求提速后的火车速度.(精确到1 km/h)
【分析】根据提速前与提速后连云港至徐州的距离不变,列出方程,求解即可.
【答案】解:设提速后的火车速度是x km/h,根据题意,
得2.3(x-260)=0.6x,
解得x=352.
答:提速后的火车速度是352 km/h.
知识点4:常见的几种应用题类型
用
知识点梳理
1.行程问题:
基本量间的关系:路程=速度×时间
相遇问题:全路程=甲走的路程+乙走的路程
追及问题:被追的路程=甲走的路程-乙走的路程(若甲为快者)
2.工程问题:
基本量间的关系:工作效率=
其他常用关系量:①甲、乙合作的工作效率=甲的工作效率+乙的工作效率;②通常把工作总量看作“1”.
典型例题
【例5】甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快,两人同时从起点同向出发,经过两人首次相遇,此时乙还需跑才能跑完第一圈.
(1)求甲、乙两人的速度分别是每分钟多少米?(列方程或者方程组解答)
(2)若两人相遇后,甲立即以每分钟的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过两人再次相遇,则乙的速度至少要提高每分钟多少米?
【分析】(1)可设乙的速度是每分钟米,则甲的速度是每分钟米,两人同向而行相遇属于追及问题,等量关系为:甲路程与乙路程的差环形场地的路程,列出方程即可求解;
(2)在环形跑道上两人背向而行属于相遇问题,等量关系为:甲路程乙路程环形场地的路程,列出算式求解即可.
【答案】解:(1)设乙的速度是每分钟米,则甲的速度是每分钟米,依题意有:
,
解得,
.
答:甲的速度是每分钟350米,乙的速度是每分钟150米.
(2)
(米,
(米.
答:乙的速度至少要提高每分钟50米.
【例6】为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作多少天?
【分析】设甲工程队每天掘进米,则乙工程队每天掘进米.根据“甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米”列出方程,然后求工作时间.
【答案】解:设甲工程队每天掘进米,则乙工程队每天掘进米,
由题意,得,
解得 ,
所以乙工程队每天掘进5米,
(天
答:甲乙两个工程队还需联合工作10天.
巩固训练
1.请写出一个解为x=2的一元一次方程:__________.
2. 若x=2是关于x的方程2x+3m-1=0的解,则m的值为________.
3. 已知关于x的方程4x-3m=2的解是x=m,则m的值是( )
A.2 B.-2 C.eq \f(2,7) D.-eq \f(2,7)
4. 一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x元,根据题意,下面所列的方程正确的是( )
A.600×0.8-x=20 B.600×8-x=20
C.600×0.8=x-20 D.600×8=x-20
5. A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B种饮料单价为x元/瓶,那么下面所列方程正确的是( )
A.2(x-1)+3x=13 B.2(x+1)+3x=13
C.2x+3(x+1)=13 D.2x+3(x-1)=13
6.在2010年“地球熄灯一小时”活动中,某地区举办烛光晚餐,设有座位x排,每排坐30人,则有8人无座位:每排坐31人,则空26个座位,则下列方程中正确的是( )
A.30x+8=31x+26 B.30x+8=31x-26
C.30x-8=31x-26 D.30x-8=31x+26
7.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员按一下喇叭,4秒后听到回响,这时汽车离山谷多远?已知空气中声音的传播速度约为340米/秒.设听到回响时,汽车离山谷x米,根据题意,列出方程为( )
A.2x+4×20=4×340 B.2x-4×72=4×340
C.2x+4×72=4×340 D.2x-4×20=4×340
8.出售甲、乙两种商品,售价都是1800元,其中甲商品能赢利20%,乙商品亏损20%,如果同时售出甲、乙商品各一件,那么( )
A.共赢利150元 B.共亏损150元
C.不盈也不亏 D.无法判断
9. 为庆祝第29届北京奥运圣火在泉州站传递,甲、乙两校联合准备文艺汇演.甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装(一人买一套)参加演出,下面是服装厂给出的演出服装的价格表:
如果两所学校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?
巩固训练参考答案
2x-2=2.
-1.
A.
A.
A.
6. B.
7. A.
8. B.
9. 解:(1)如果甲、乙两校联合起来购买服装需40×92=3680(元)
比各自购买服装共可以节省:5000-3680=1320(元);
(2)设甲校有学生人(依题意,则乙校有学生人.
依题意得:,
解得:.
经检验符合题意.
(人.
故甲校有52人,乙校有40人.
(3)方案一:各自购买服装需(元;
方案二:联合购买服装需(元;
方案三:联合购买91套服装需(元;
综上所述:因为4980元元元.
所以应该甲乙两校联合起来选择按40元一次购买91套服装最省钱.考点
课标要求
考查角度
1
一元一次方程相关概念及解法
了解方程、一元一次方程的概念,会解一元一次方程.
考查方程的解、解方程、列方程等基础知识.
常以选择题、填空题的形式.
2
解一元一次方程
能够根据具体问题中的数量关系,列出一元一次方程解决实际问题,能根据具体问题的实际意义,检验结果是否合理.
以列方程解应用题的形式考查解方程的基本思想和列方程解应用题的能力.
常以选择、填空题、解答题的形式命题.
购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
相关学案
这是一份【中考一轮复习】2023年中考数学总复习学案——专题06 一元一次方程(原卷版+解析版),文件包含专题07二元一次方程组归纳与讲解解析版docx、专题07二元一次方程组归纳与讲解原卷版docx等2份学案配套教学资源,其中学案共32页, 欢迎下载使用。
这是一份备考2022中考数学一轮专题复习学案25 概率,共14页。
这是一份备考2022中考数学一轮专题复习学案24 统计,共16页。