




专题七 双曲线问题-2022年中考数学二轮复习之重难热点提分专题
展开专题七 双曲线问题
1.(2021连云港)如图,在平面直角坐标系xOy中,反比例函数(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m= ,点C的坐标为 ;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数图象于点E,求△ODE面积的最大值.
【分析】(1)根据待定系数法即可求得m的值,根据A点的坐标即可求得C的坐标;
(2)根据待定系数法求得直线AB的解析式,设出D、E的坐标,然后根据三角形面积公式得到S△ODE(x﹣1)2,由二次函数的性质即可求得结论.
【解析】(1)∵反比例函数y(x>0)的图象经过点A(4,),
∴m6,
∵AB交x轴于点C,C为线段AB的中点.
∴C(2,0);
故答案为6,(2,0);
(2)设直线AB的解析式为y=kx+b,
把A(4,),C(2,0)代入得,解得,
∴直线AB的解析式为yx;
∵点D为线段AB上的一个动点,
∴设D(x,x)(0<x≤4),
∵DE∥y轴,
∴E(x,),
∴S△ODEx•(x)x2x+3(x﹣1)2,
∴当x=1时,△ODE的面积的最大值为.
2.(2021成都)在平面直角坐标系xOy中,反比例函数(x>0)的图象经过点A(3,4),过点A的直线y=kx+b与x轴、y轴分别交于B,C两点.
(1)求反比例函数的表达式;
(2)若△AOB的面积为△BOC的面积的2倍,求此直线的函数表达式.
【分析】(1)把A(3,4)代入y(x>0)即可得到结论;
(2)根据题意得到B(,0),C(0,b),根据三角形的面积公式列方程即可得到结论.
【解析】(1)∵反比例函数y(x>0)的图象经过点A(3,4),
∴k=3×4=12,
∴反比例函数的表达式为y;
(2)∵直线y=kx+b过点A,
∴3k+b=4,
∵过点A的直线y=kx+b与x轴、y轴分别交于B,C两点,
∴B(,0),C(0,b),
∵△AOB的面积为△BOC的面积的2倍,
∴4×||=2||×|b|,
∴b=±2,
当b=2时,k,
当b=﹣2时,k=2,
∴直线的函数表达式为:yx+2,y=2x﹣2.
3.(2021遂宁)如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线(k≠0)于D、E两点,连结CE,交x轴于点F.
(1)求双曲线(k≠0)和直线DE的解析式.
(2)求△DEC的面积.
【分析】(1)作DM⊥y轴于M,通过证得△AOB≌△DMA(AAS),求得D的坐标,然后根据待定系数法即可求得双曲线y(k≠0)和直线DE的解析式.
(2)解析式联立求得E的坐标,然后根据勾股定理求得DE和DB,进而求得CN的长,即可根据三角形面积公式求得△DEC的面积.
【解析】∵点A的坐标为(0,2),点B的坐标为(1,0),
∴OA=2,OB=1,
作DM⊥y轴于M,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∴∠OAB+∠DAM=90°,
∵∠OAB+∠ABO=90°,
∴∠DAM=∠ABO,
在△AOB和△DMA中
,
∴△AOB≌△DMA(AAS),
∴AM=OB=1,DM=OA=2,
∴D(2,3),
∵双曲线y═(k≠0)经过D点,
∴k=2×3=6,
∴双曲线为y,
设直线DE的解析式为y=mx+n,
把B(1,0),D(2,3)代入得,解得,
∴直线DE的解析式为y=3x﹣3;
(2)连接AC,交BD于N,
∵四边形ABCD是正方形,
∴BD垂直平分AC,AC=BD,
解得或,
∴E(﹣1,﹣6),
∵B(1,0),D(2,3),
∴DE3,DB,
∴CNBD,
∴S△DECDE•CN.
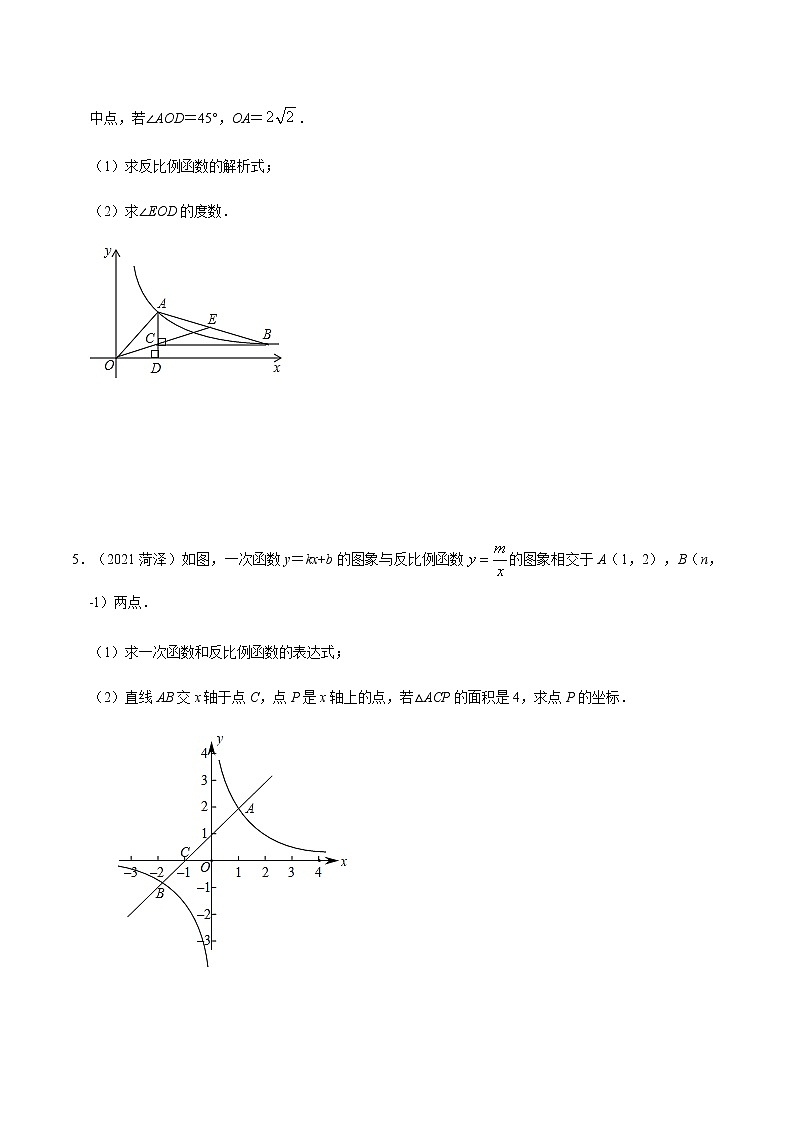
4.(2021江西)如图,Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数(x>0)的图象上,直线AC⊥x轴,垂足为D,连结OA,OC,并延长OC交AB于点E,当AB=2OA时,点E恰为AB的中点,若∠AOD=45°,OA=.
(1)求反比例函数的解析式;
(2)求∠EOD的度数.
【分析】(1)根据题意求得A(2,2),然后代入y(x>0),求得k的值,即可求得反比例函数的解析式;
(2)根据AB=2OA时,点E恰为AB的中点,得出OA=AE=BE,根据直角三角形斜边中线的性质得出CE=AE=BE,根据等腰三角形的性质越久三角形外角的性质即可得出∠AOE=2∠EOD,从而求得∠EOD=15°.
【解析】(1)∵直线AC⊥x轴,垂足为D,∠AOD=45°,
∴△AOD是等腰直角三角形,
∵OA=2,
∴OD=AD=2,
∴A(2,2),
∵顶点A在反比例函数y(x>0)的图象上,
∴k=2×2=4,
∴反比例函数的解析式为y;
(2)∵AB=2OA,点E恰为AB的中点,
∴OA=AE,
∵Rt△ABC中,∠ACB=90°,
∴CE=AE=BE,
∴∠AOE=∠AEO,∠ECB=∠EBC,
∵∠AEO=∠ECB+∠EBC=2∠EBC,
∵BC∥x轴,
∴∠EOD=∠ECB,
∴∠AOE=2∠EOD,
∵∠AOE=45°,
∴∠EOD=15°.
5.(2021菏泽)如图,一次函数y=kx+b的图象与反比例函数的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
【分析】(1)先根据点A坐标求出反比例函数解析式,再求出点B的坐标,继而根据点A、B坐标可得直线解析式;
(2)先根据直线解析式求出点C的坐标,再设P(m,0),知PC=|﹣1﹣m|,根据S△ACP•PC•yA=4求出m的值即可得出答案.
【解析】(1)将点A(1,2)代入y,得:m=2,
∴y,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得:,
解得,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(m,0),
则PC=|﹣1﹣m|,
∵S△ACP•PC•yA=4,
∴|﹣1﹣m|×2=4,
解得m=3或m=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
6.(2021泰安)如图,已知一次函数y=kx+b的图象与反比例函数的图象交于点A(3,a),点B(14﹣2a,2).
(1)求反比例函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,求△ACD的面积.
【分析】(1)点A(3,a),点B(14﹣2a,2)在反比例函数上,则3×a=(14﹣2a)×2,即可求解;
(2)a=4,故点A、B的坐标分别为(3,4)、(6,2),求出一次函数的表达式为:yx+6,则点C(0,6),故OC=6,进而求解.
【解析】(1)∵点A(3,a),点B(14﹣2a,2)在反比例函数上,
∴3×a=(14﹣2a)×2,解得:a=4,则m=3×4=12,
故反比例函数的表达式为:y;
(2)∵a=4,故点A、B的坐标分别为(3,4)、(6,2),
设直线AB的表达式为:y=kx+b,则,解得,
故一次函数的表达式为:yx+6;
当x=0时,y=6,故点C(0,6),故OC=6,
而点D为点C关于原点O的对称点,则CD=2OC=12,
△ACD的面积CD•xA12×3=18.
7.(2021枣庄)如图,在平面直角坐标系中,一次函数和y=﹣2x的图象相交于点A,反比例函数的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数的图象与反比例函数的图象的另一个交点为B,连接OB,求△ABO的面积.
【分析】(1)联立yx+5①和y=﹣2x并解得:,故点A(﹣2.4),进而求解;
(2)S△AOB=S△AOC﹣S△BOCOC•AMOC•BN,即可求解.
【解析】(1)联立yx+5①和y=﹣2x并解得:,故点A(﹣2.4),
将点A的坐标代入反比例函数表达式得:4,解得:k=﹣8,
故反比例函数表达式为:y②;
(2)联立①②并解得:x=﹣2或﹣8,
当x=﹣8时,yx+5=1,故点B(﹣8,1),
设yx+5交x轴于点C(﹣10,0),过点A、B分别作x轴的垂线交于点M、N,
则S△AOB=S△AOC﹣S△BOCOC•AMOC•BN.
8.(2021广东)如图,点B是反比例函数(x>0)图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数(x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)填空:k= ;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
【分析】(1)设点B(s,t),st=8,则点M(s,t),则ks•tst=2;
(2)△BDF的面积=△OBD的面积=S△BOA﹣S△OAD,即可求解;
(3)确定直线DE的表达式为:y,令y=0,则x=5m,故点F(5m,0),即可求解.
【解析】(1)设点B(s,t),st=8,则点M(s,t),
则ks•tst=2,
故答案为2;
(2)△BDF的面积=△OBD的面积=S△BOA﹣S△OAD82=3;
(3)设点D(m,),则点B(4m,),
∵点G与点O关于点C对称,故点G(8m,0),
则点E(4m,),
设直线DE的表达式为:y=sx+n,将点D、E的坐标代入上式得,解得,
故直线DE的表达式为:y,令y=0,则x=5m,故点F(5m,0),
故FG=8m﹣5m=3m,而BD=4m﹣m=3m=FG,
则FG∥BD,故四边形BDFG为平行四边形.
9.(2021绥化)如图,在矩形OABC中,AB=2,BC=4,点D是边AB的中点,反比例函数(x>0)的图象经过点D,交BC边于点E,直线DE的解析式为y2=mx+n(m≠0).
(1)求反比例函数(x>0)的解析式和直线DE的解析式;
(2)在y轴上找一点P,使△PDE的周长最小,求出此时点P的坐标;
(3)在(2)的条件下,△PDE的周长最小值是 .
【分析】(1)根据线段中点的定义和矩形的性质得到D(1,4),解方程和方程组即可得到结论;
(2)作点D关于y轴的对称点D′,连接D′E交y轴于P,连接PD,此时,△PDE的周长最小,求得直线D′E的解析式为yx,于是得到结论;
(3)根据勾股定理即可得到结论.
【解析】(1)∵点D是边AB的中点,AB=2,
∴AD=1,
∵四边形OABC是矩形,BC=4,
∴D(1,4),
∵反比例函数y1(x>0)的图象经过点D,
∴k=4,
∴反比例函数的解析式为y(x>0),
当x=2时,y=2,
∴E(2,2),
把D(1,4)和E(2,2)代入y2=mx+n(m≠0)得,,
∴,
∴直线DE的解析式为y=﹣2x+6;
(2)作点D关于y轴的对称点D′,连接D′E交y轴于P,连接PD,
此时,△PDE的周长最小,
∵D点的坐标为(1,4),
∴D′的坐标为(﹣1,4),
设直线D′E的解析式为y=ax+b,
∴,解得:,
∴直线D′E的解析式为yx,
令x=0,得y,
∴点P的坐标为(0,);
(3)∵D(1,4),E(2,2),
∴BE=2,BD=1,
∴DE,
由(2)知,D′的坐标为(﹣1,4),
∴BD′=3,
∴D′E,
∴△PDE的周长最小值=DE+D′E,
故答案为:.
专题五 商品最大利润问题-2022年中考数学二轮复习之重难热点提分专题: 这是一份专题五 商品最大利润问题-2022年中考数学二轮复习之重难热点提分专题,文件包含专题五商品最大利润问题-2022年中考数学二轮复习之重难热点提分专题解析版docx、专题五商品最大利润问题-2022年中考数学二轮复习之重难热点提分专题原卷版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
专题四 最佳方案问题-2022年中考数学二轮复习之重难热点提分专题: 这是一份专题四 最佳方案问题-2022年中考数学二轮复习之重难热点提分专题,文件包含专题四最佳方案问题-2022年中考数学二轮复习之重难热点提分专题解析版docx、专题四最佳方案问题-2022年中考数学二轮复习之重难热点提分专题原卷版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
专题十一 几何动点问题-2022年中考数学二轮复习之重难热点提分专题: 这是一份专题十一 几何动点问题-2022年中考数学二轮复习之重难热点提分专题,文件包含专题十一几何动点问题-2022年中考数学二轮复习之重难热点提分专题解析版docx、专题十一几何动点问题-2022年中考数学二轮复习之重难热点提分专题原卷版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。












