2022年 人教版数学九年级中考第一轮专题训练 函数及其图象

这是一份2022年 人教版数学九年级中考第一轮专题训练 函数及其图象，共9页。
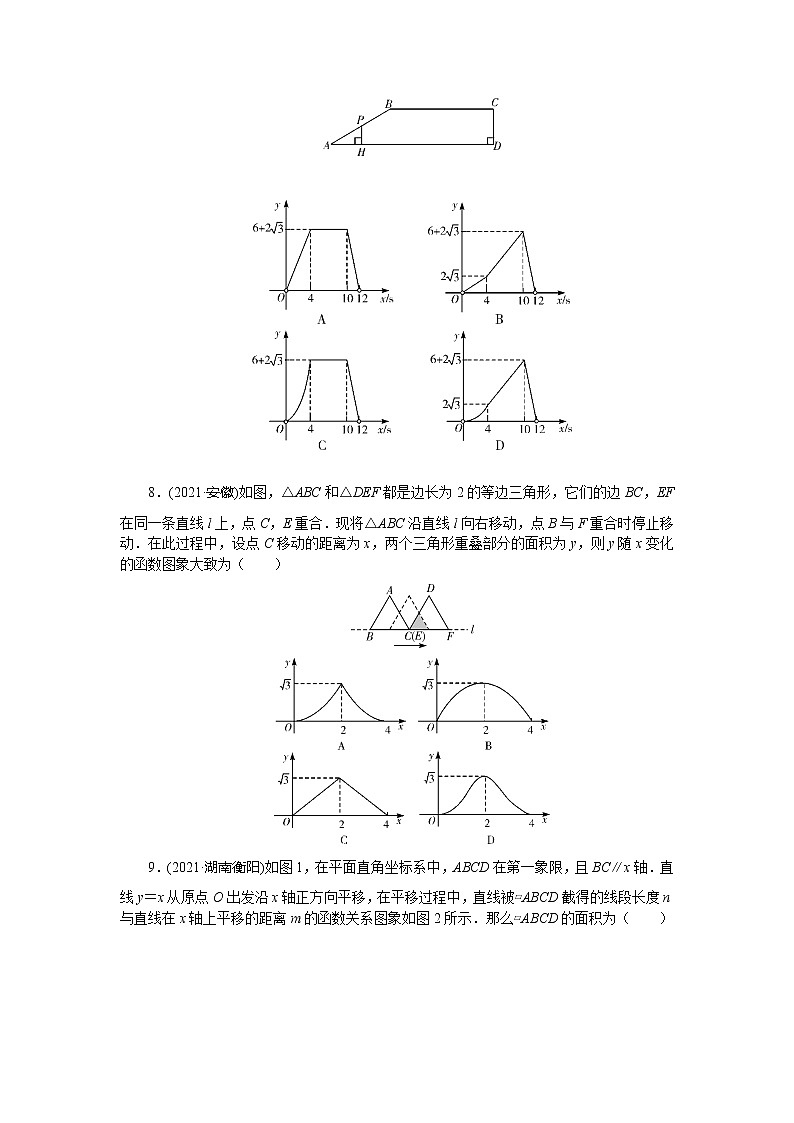
　函数及其图象　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　命题点1　平面直角坐标系中点的坐标特征1．(2021·四川凉山州)点P(2，3)关于x轴对称的点P′的坐标是（    ）A．(2，－3)     B．(－2，3)    C．(－2，－3)    　 D．(3，2)2．(2021·贵州黔东南州)以▱ABCD对角线的交点O为原点，平行于BC边的直线为x轴，建立如图所示的平面直角坐标系．若A点坐标为(－2，1)，则C点坐标为             ．3．(2021·山东枣庄)如图，在平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2.将△AOB绕点O逆时针旋转90°，则点B的对应点B′的坐标是（    ）A．(－，3)     B．(－3，)C．(－，2＋)     D．(－1，2＋)命题点2　函数自变量的取值范围4．(2021·四川遂宁)函数y＝中，自变量x的取值范围是（    ）A．x＞－2 B．x≥－2C．x＞－2且x≠1 D．x≥－2且x≠15．(2021·黑龙江鸡西)在函数y＝中，自变量x的取值范围是            _．6．(2021·甘肃天水)已知函数y＝，则自变量x的取值范围是           ．命题点3　函数图象的分析与判断7．(2021·湖北孝感)如图，在四边形ABCD中，AD∥BC，∠D＝90°，AB＝4，BC＝6，∠BAD＝30°.动点P从点A出发，沿路径A→B→C→D，以每秒1个单位长度的速度向点D运动．过点P作PH⊥AD，垂足为H.设点P运动的时间为x(单位：s)，△APH的面积为y，则y关于x的函数图象大致是（    ）   8．(2021·安徽)如图，△ABC和△DEF都是边长为2的等边三角形，它们的边BC，EF在同一条直线l上，点C，E重合．现将△ABC沿直线l向右移动，点B与F重合时停止移动．在此过程中，设点C移动的距离为x，两个三角形重叠部分的面积为y，则y随x变化的函数图象大致为（    ） 9．(2021·湖南衡阳)如图1，在平面直角坐标系中，ABCD在第一象限，且BC∥x轴．直线y＝x从原点O出发沿x轴正方向平移，在平移过程中，直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数关系图象如图2所示．那么▱ABCD的面积为（    ）A.3 B．3C．6 D．6 1．(2021·贵州毕节)在平面直角坐标系中，第二象限内有一点M，点M到x轴的距离为5，到y轴的距离为4，则点M的坐标是（    ）A．(5，4)     B．(4，5)    C．(－4，5)     D．(－5，4) 2．(2021·江苏泰州)以水平数轴的原点O为圆心，过正半轴Ox上的每一刻度点画同心圆，将Ox逆时针依次旋转30°，60°，90°，…，330°得到11条射线，构成如图所示的“圆”坐标系，点A，B的坐标分别表示为(5，0°)，(4，300°)，则点C的坐标应表示为           ． 3．(2021·新疆)如图，在x轴，y轴上分别截取OA，OB，使OA＝OB，再分别以点A，B为圆心，以大于AB的长为半径画弧，两弧交于点P.若点P的坐标为(a，2a－3)，则a的值为           ． 4．(2021·江苏苏州)如图，在平面直角坐标系中，点A，B的坐标分别为(－4，0)，(0，4)，点C(3，n)在第一象限内，连接AC，BC.已知∠BCA＝2∠CAO，则n＝           ．5．(2021·山东威海)如图1，某广场地面是用A，B，C三种类型地砖平铺而成的．三种类型地砖上表面图案如图2所示．现用有序数对表示每一块地砖的位置：第一行的第一块(A型)地砖记作(1，1)，第二块(B型)地砖记作(2，1)…若(m，n)位置恰好为A型地砖，则正整数m，n须满足的条件是                        _．6．(2021·江苏南通)如图1，E为矩形ABCD的边AD上一点，点P从点B出发沿折线B－E－D运动到点D停止，点Q从点B出发沿BC运动到点C停止，它们的运动速度都是1cm/s.现P，Q两点同时出发，设运动时间为x(s)，△BPQ的面积为y(cm2)，若y与x的对应关系如图2所示，则矩形ABCD的面积是（    ）A．96cm2 B．84cm2C．72cm2 D．56cm27．(2021·北京)小云在学习过程中遇到一个函数y＝|x|(x2－x＋1)(x≥－2).下面是小云对其探究的过程，请补充完整：(1)当－2≤x＜0时，对于函数y1＝|x|，有y1＝－x，当－2≤x＜0时，y1随x的增大而__           ，且y1＞0；对于函数y2＝x2－x＋1，当－2≤x＜0时，y2随x的增大而_           __，且y2＞0.结合上述分析，进一步探究发现，对于函数y，当－2≤x＜0时，y随x的增大而_           __．(2)当x≥0时，对于函数y，y与x的几组对应值如下表： x0123…y01…结合上表，进一步探究发现，当x≥0时，y随x的增大而增大．在如图所示的平面直角坐标系xOy中，画出当x≥0时的函数y的图象．(3)过点(0，m)(m＞0)作平行于x轴的直线l，结合(1)(2)的分析，解决问题：若直线l与函数y＝|x|(x2－x＋1)(x≥－2)的图象有两个交点，则m的最大值是_           ．            　函数及其图象　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　命题点1　平面直角坐标系中点的坐标特征1．(2021·四川凉山州)点P(2，3)关于x轴对称的点P′的坐标是(　A　)A．(2，－3)     B．(－2，3)    C．(－2，－3)    　 D．(3，2)2．(2021·贵州黔东南州)以▱ABCD对角线的交点O为原点，平行于BC边的直线为x轴，建立如图所示的平面直角坐标系．若A点坐标为(－2，1)，则C点坐标为__(2，－1)__．3．(2021·山东枣庄)如图，在平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2.将△AOB绕点O逆时针旋转90°，则点B的对应点B′的坐标是(　A　)A．(－，3)     B．(－3，)C．(－，2＋)     D．(－1，2＋)命题点2　函数自变量的取值范围4．(2021·四川遂宁)函数y＝中，自变量x的取值范围是(　D　)A．x＞－2 B．x≥－2C．x＞－2且x≠1 D．x≥－2且x≠15．(2021·黑龙江鸡西)在函数y＝中，自变量x的取值范围是__x＞0.5__．6．(2021·甘肃天水)已知函数y＝，则自变量x的取值范围是__x≥－2且x≠3__．命题点3　函数图象的分析与判断7．(2021·湖北孝感)如图，在四边形ABCD中，AD∥BC，∠D＝90°，AB＝4，BC＝6，∠BAD＝30°.动点P从点A出发，沿路径A→B→C→D，以每秒1个单位长度的速度向点D运动．过点P作PH⊥AD，垂足为H.设点P运动的时间为x(单位：s)，△APH的面积为y，则y关于x的函数图象大致是(　D　)   8．(2021·安徽)如图，△ABC和△DEF都是边长为2的等边三角形，它们的边BC，EF在同一条直线l上，点C，E重合．现将△ABC沿直线l向右移动，点B与F重合时停止移动．在此过程中，设点C移动的距离为x，两个三角形重叠部分的面积为y，则y随x变化的函数图象大致为(　A　) 9．(2021·湖南衡阳)如图1，在平面直角坐标系中，ABCD在第一象限，且BC∥x轴．直线y＝x从原点O出发沿x轴正方向平移，在平移过程中，直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数关系图象如图2所示．那么▱ABCD的面积为(　B　)A.3 B．3C．6 D．6 1．(2021·贵州毕节)在平面直角坐标系中，第二象限内有一点M，点M到x轴的距离为5，到y轴的距离为4，则点M的坐标是(　C　)A．(5，4)     B．(4，5)    C．(－4，5)     D．(－5，4) 2．(2021·江苏泰州)以水平数轴的原点O为圆心，过正半轴Ox上的每一刻度点画同心圆，将Ox逆时针依次旋转30°，60°，90°，…，330°得到11条射线，构成如图所示的“圆”坐标系，点A，B的坐标分别表示为(5，0°)，(4，300°)，则点C的坐标应表示为__(3，240°)__． 3．(2021·新疆)如图，在x轴，y轴上分别截取OA，OB，使OA＝OB，再分别以点A，B为圆心，以大于AB的长为半径画弧，两弧交于点P.若点P的坐标为(a，2a－3)，则a的值为__3__． 4．(2021·江苏苏州)如图，在平面直角坐标系中，点A，B的坐标分别为(－4，0)，(0，4)，点C(3，n)在第一象限内，连接AC，BC.已知∠BCA＝2∠CAO，则n＝____．5．(2021·山东威海)如图1，某广场地面是用A，B，C三种类型地砖平铺而成的．三种类型地砖上表面图案如图2所示．现用有序数对表示每一块地砖的位置：第一行的第一块(A型)地砖记作(1，1)，第二块(B型)地砖记作(2，1)…若(m，n)位置恰好为A型地砖，则正整数m，n须满足的条件是__m，n同为奇数或m，n同为偶数__．6．(2021·江苏南通)如图1，E为矩形ABCD的边AD上一点，点P从点B出发沿折线B－E－D运动到点D停止，点Q从点B出发沿BC运动到点C停止，它们的运动速度都是1cm/s.现P，Q两点同时出发，设运动时间为x(s)，△BPQ的面积为y(cm2)，若y与x的对应关系如图2所示，则矩形ABCD的面积是(　C　)A．96cm2 B．84cm2C．72cm2 D．56cm27．(2021·北京)小云在学习过程中遇到一个函数y＝|x|(x2－x＋1)(x≥－2).下面是小云对其探究的过程，请补充完整：(1)当－2≤x＜0时，对于函数y1＝|x|，有y1＝－x，当－2≤x＜0时，y1随x的增大而__减小__，且y1＞0；对于函数y2＝x2－x＋1，当－2≤x＜0时，y2随x的增大而__减小__，且y2＞0.结合上述分析，进一步探究发现，对于函数y，当－2≤x＜0时，y随x的增大而__减小__．(2)当x≥0时，对于函数y，y与x的几组对应值如下表： x0123…y01…结合上表，进一步探究发现，当x≥0时，y随x的增大而增大．在如图所示的平面直角坐标系xOy中，画出当x≥0时的函数y的图象．(3)过点(0，m)(m＞0)作平行于x轴的直线l，结合(1)(2)的分析，解决问题：若直线l与函数y＝|x|(x2－x＋1)(x≥－2)的图象有两个交点，则m的最大值是____．解：(1)减小　减小　减小(2)x≥0时的函数y的图象如图所示：(3)∵直线l与函数y＝|x|(x2－x＋1)(x≥－2)的图象有两个交点，观察图象可知，x＝－2时，m的值最大，m最大＝×2×(4＋2＋1)＝.故答案为.