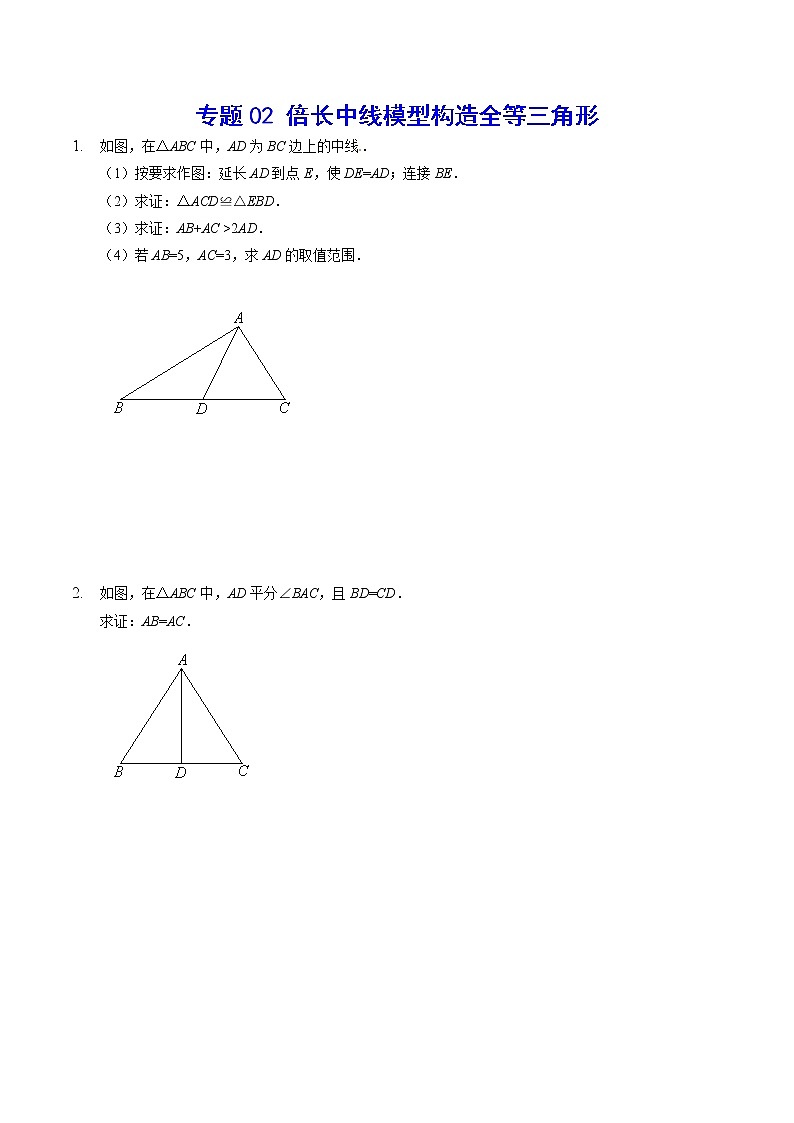
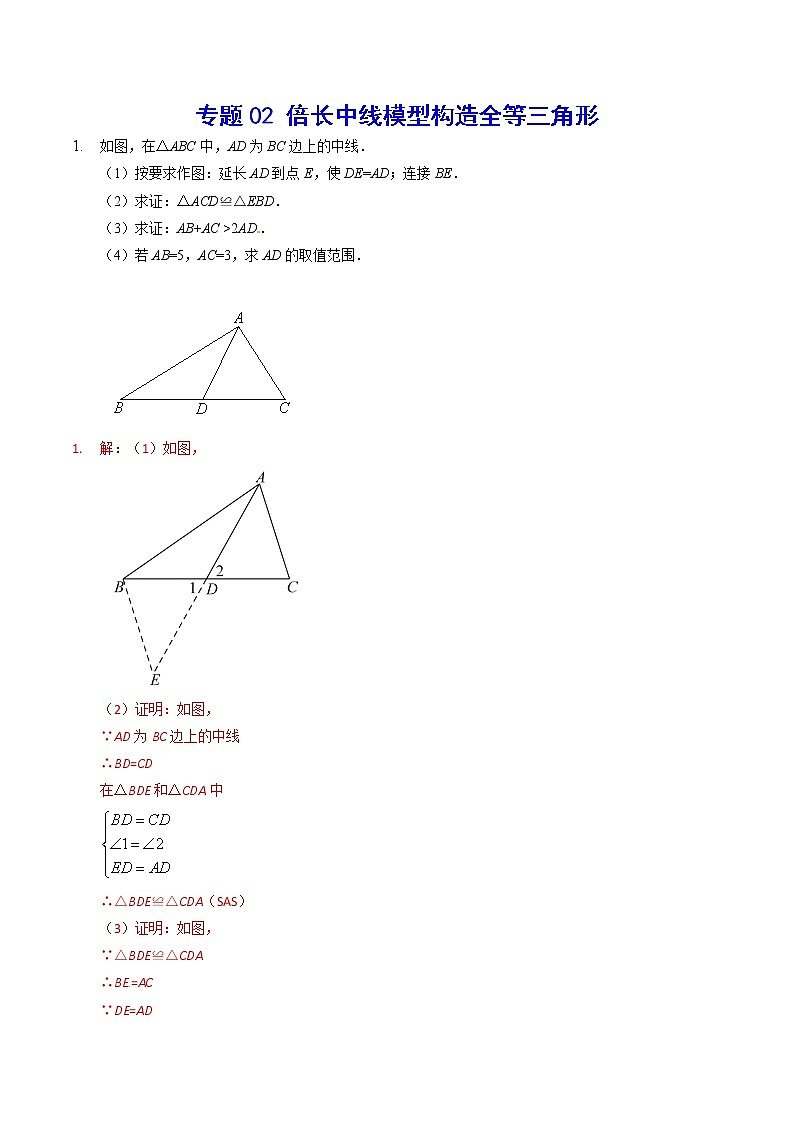


专题02 倍长中线模型构造全等三角形(提升训练)-2022年中考数学重难点专项突破(全国通用)
展开(1)按要求作图:延长AD到点E,使DE=AD;连接BE.
(2)求证:△ACD≌△EBD.
(3)求证:AB+AC >2AD.
(4)若AB=5,AC=3,求AD的取值范围.
解:(1)如图,
(2)证明:如图,
∵AD为BC边上的中线
∴BD=CD
在△BDE和△CDA中
∴△BDE≌△CDA(SAS)
(3)证明:如图,
∵△BDE≌△CDA
∴BE=AC
∵DE=AD
∴AE=2 AD
在△ABE中,AB+BE>AE
∴AB+AC>2AD
(4)在△ABE中,
ABBE
∵AC=3,AB=5
∴53
∴1
求证:AB=AC.
证明:如图,延长AD到E,使DE=AD,连接BE
在△ADC和△EDB中
∴△ADC≌△EDB(SAS)
∴AC=EB,∠2=∠E
∵AD平分∠BAC
∴∠1=∠2
∴∠1=∠E
∴AB=BE
∴AB=AC
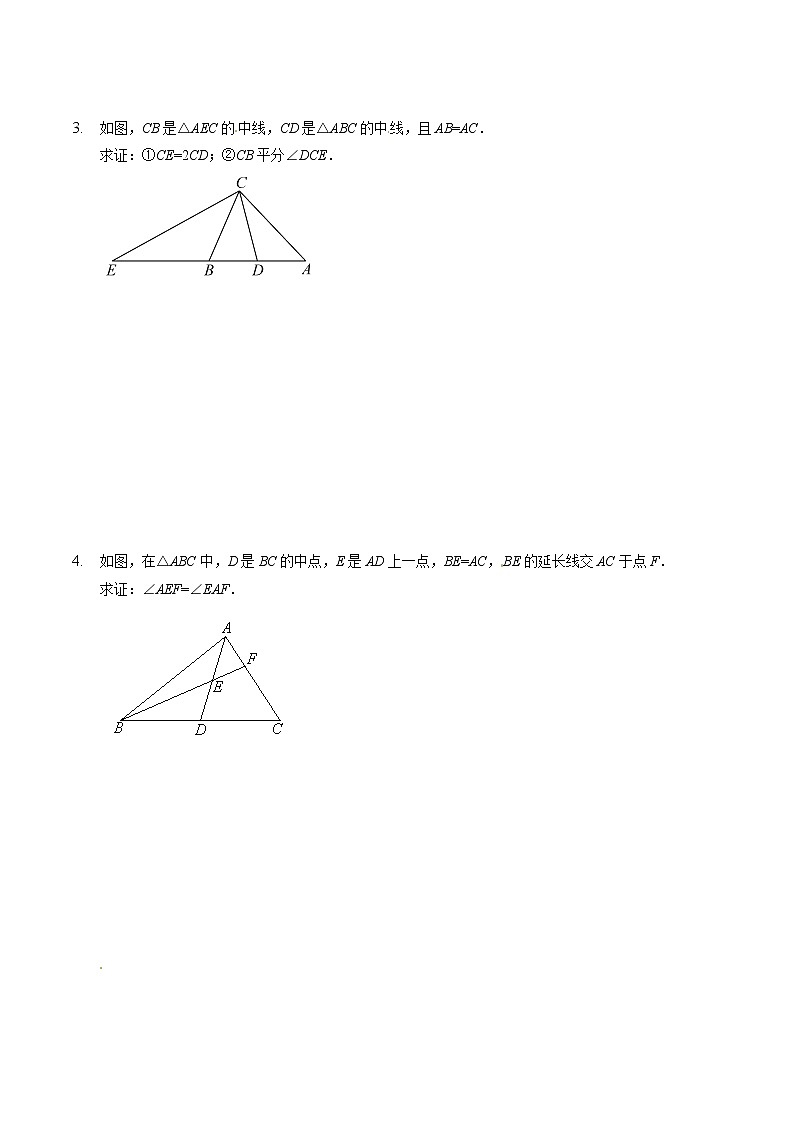
如图,CB是△AEC的中线,CD是△ABC的中线,且AB=AC.
求证:①CE=2CD;②CB平分∠DCE.
证明:如图,延长CD到F,使DF=CD,连接BF
∴CF=2CD
∵CD是△ABC的中线
∴BD=AD
在△BDF和△ADC中
∴△BDF≌△ADC(SAS)
∴BF=AC,∠1=∠F
∵CB是△AEC的中线
∴BE=AB
∵AC=AB
∴BE=BF
∵∠1=∠F
∴BF∥AC
∴∠1+∠2+∠5+∠6=180°
又∵AC=AB
∴∠1+∠2=∠5
又∵∠4+∠5=180°
∴∠4=∠5+∠6
即∠CBE=∠CBF
在△CBE和△CBF中
∴△CBE≌△CBF(SAS)
∴CE=CF,∠2=∠3
∴CE=2CD
CB平分∠DCE
如图,在△ABC中,D是BC的中点,E是AD上一点,BE=AC,BE的延长线交AC于点F.
求证:∠AEF=∠EAF.
证明:如图,延长AD到M,使DM=AD,连接BM
∵D是BC边的中点
∴BD=CD
在△ADC和△MDB中
∴△ADC≌△MDB(SAS)
∴∠1=∠M,AC=MB
∵BE=AC
∴BE=MB
∴∠M=∠3
∴∠1=∠3
∵∠3=∠2
∴∠1=∠2
即∠AEF=∠EAF
如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交AB于点G,BG=CF.
求证:AD为△ABC的角平分线.
证明:如图,延长FE到M,使EM=EF,连接BM
∵点E是BC的中点
∴BE=CE
在△CFE和△BME中
∴△CFE≌△BME(SAS)
∴CF=BM,∠F=∠M
∵BG=CF
∴BG=BM
∴∠1=∠M
∴∠1=∠F
∵AD∥EF
∴∠3=∠F,∠1=∠2
∴∠2=∠3
即AD为△ABC的角平分线
如图,在四边形ABCD中,AD∥BC,点E在BC上,点F是CD的中点,且AF⊥AB,已知AD=2.7,AE=BE=5,求CE的长.
解:如图,延长AF交BC的延长线于点G
∵AD∥BC
∴∠3=∠G
∵点F是CD的中点
∴DF=CF
在△ADF和△GCF中
∴△ADF≌△GCF(AAS)
∴AD=CG
∵AD=2.7
∴CG=2.7
∵AE=BE
∴∠1=∠B
∵AB⊥AF
∴∠1+∠2=90°
∠B+∠G=90°
∴∠2=∠G
∴EG=AE=5
∴CE=EGCG
=52.7
=2.3
如图,在正方形ABCD中,CD=BC,∠DCB=90°,点E在CB的延长线上,过点E作EF⊥BE,且EF=BE.连接BF,FD,取FD的中点G,连接EG,CG.
求证:EG=CG且EG⊥CG.
证明:如图,延长EG交CD的延长线于点M
由题意,∠FEB=90°,∠DCB=90°
∴∠DCB+∠FEB=180°
∴EF∥CD
∴∠FEG=∠M
∵点G为FD的中点
∴FG=DG
在△FGE和△DGM中
∴△FGE≌△DGM(AAS)
∴EF=MD,EG=MG
∵△FEB是等腰直角三角形
∴EF=EB
∴BE=MD
在正方形ABCD中,BC=CD
∴BE+BC=MD+CD
即EC=MC
∴△ECM是等腰直角三角形
∵EG=MG
∴EG⊥CG,∠3=∠4=45°
∴∠2=∠3=45°
∴EG=CG
专题03 一线三垂直模型构造全等三角形(提升训练)-2024年中考数学重难点专项突破(全国通用): 这是一份专题03 一线三垂直模型构造全等三角形(提升训练)-2024年中考数学重难点专项突破(全国通用),文件包含专题03一线三垂直模型构造全等三角形提升训练原卷版docx、专题03一线三垂直模型构造全等三角形提升训练解析版docx等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
专题02 倍长中线模型构造全等三角形(提升训练)-2024年中考数学重难点专项突破(全国通用): 这是一份专题02 倍长中线模型构造全等三角形(提升训练)-2024年中考数学重难点专项突破(全国通用),文件包含专题02倍长中线模型构造全等三角形提升训练原卷版docx、专题02倍长中线模型构造全等三角形提升训练解析版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
专题09 倍长中线模型综合应用(专项训练)-备战中考数学《重难点解读•专项训练》(全国通用): 这是一份专题09 倍长中线模型综合应用(专项训练)-备战中考数学《重难点解读•专项训练》(全国通用),文件包含专题09倍长中线模型综合应用专项训练解析版docx、专题09倍长中线模型综合应用专项训练原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












