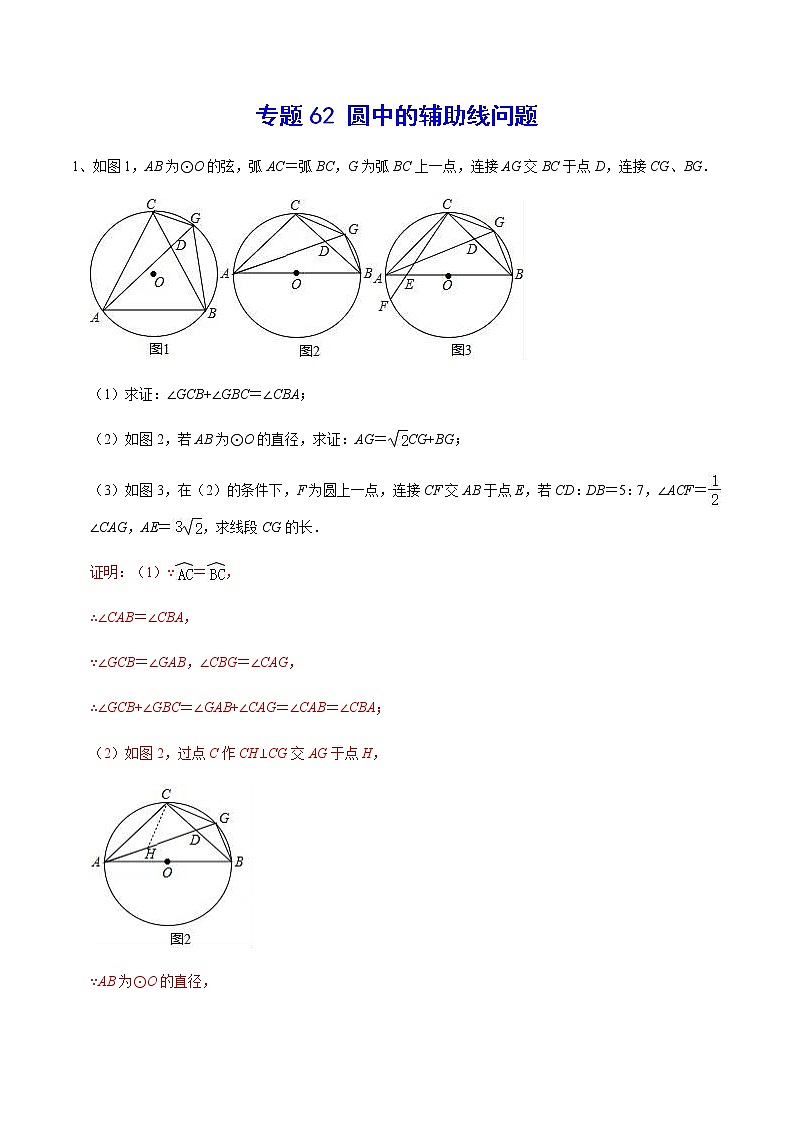
专题62 圆中的辅助线问题-2022年中考数学重难点专项突破（全国通用）

这是一份专题62 圆中的辅助线问题-2022年中考数学重难点专项突破（全国通用），文件包含专题62圆中的辅助线问题解析版docx、专题62圆中的辅助线问题原卷版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。


（1）求证：∠GCB+∠GBC＝∠CBA；
（2）如图2，若AB为⊙O的直径，求证：AG＝CG+BG；
（3）如图3，在（2）的条件下，F为圆上一点，连接CF交AB于点E，若CD：DB＝5：7，∠ACF＝∠CAG，AE＝，求线段CG的长．
证明：（1）∵＝，
∴∠CAB＝∠CBA，
∵∠GCB＝∠GAB，∠CBG＝∠CAG，
∴∠GCB+∠GBC＝∠GAB+∠CAG＝∠CAB＝∠CBA；
（2）如图2，过点C作CH⊥CG交AG于点H，
∵AB为⊙O的直径，
∴∠AGB＝∠ACB＝90°，且AC＝BC，
∴∠ABC＝∠BAC＝45°．
∵∠AGC＝∠ABC，
∴∠AGC＝45°，且CH⊥CG，
∴∠CHG＝∠AGC＝45°，
∴CH＝CG，∠AHC＝135°
∴GH＝CG．
∵∠CGB＝∠CGA+∠AGB＝135°，
∴∠AHC＝∠CGB，CH＝CG，∠CAH＝∠CBG，
∴△ACH≌△BCG（AAS）
∴AH＝BG，
∴AG＝CG+BG；
（3）∵CD：DB＝5：7，
∴设CD＝5a，DB＝7a，
∴BC＝AC＝12a，
∴AD＝＝＝13a．
如图3，过点E作EH⊥AC于H，作AP平分∠GAC，交BC于P，作PQ⊥AD于Q，
∴∠CAP＝∠DAP＝∠CAG，∠PQA＝90°＝∠ACB，且AP＝AP，
∴△CAP≌△QAP（AAS）
∴AC＝AQ＝12a，CP＝PQ，
∴QD＝AD﹣AQ＝a．
∵PD2＝PQ2+QD2，
∴（5﹣PQ）2＝PQ2+a2，
∴PQ＝a，
∴CP＝a，
∵HE⊥AC，∠CAB＝45°，
∴∠HEA＝∠CAB＝45°，
∴AH＝HE，
∵AE2＝AH2+HE2＝（3）2，
∴AH＝HE＝3，
∵∠ACF＝∠CAG，∠CAP＝∠DAP＝∠CAG，
∴∠ACF＝∠CAP，
∴tan∠CAP＝tan∠ACF＝，
∴
∴CH＝15，
∴AC＝3+15＝18＝12a，
∴a＝，
∴CD＝，BD＝，AD＝．
∵∠ACD＝∠AGB＝90°，∠CAD＝∠DBG，
∴△ACD∽△BGD，
∴，
∴，
∴BG＝，DG＝，
∴AG＝AD+DG＝+＝，
∵AG＝CG+BG，
∴＝＝CG，
∴CG＝．
2、如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC平分∠BAD，过C点作CE⊥AD延长线于E点．
（1）求证：CE是⊙O的切线；
（2）若AB＝10，AC＝8，求AD的长．
解：（1）连接OC，
∵OC＝OA，
∴∠OAC＝∠OCA，
又∵AC平分∠BAD，
∴∠CAD＝∠CAO＝∠OCA，
∴OC∥AE，
∵CE⊥AD，
即可得OC⊥CE，
∴CE是⊙O的切线；
（2）∵AB是⊙O的直径，
∴∠ACB＝90°，
∴BC＝＝＝6，
∵∠BAC＝∠DAC，
∴＝，
∴BC＝CD＝6，
延长BC交AE的延长线于F，
∵∠BAC＝∠FAC，AC＝AC，∠ACB＝∠ACF＝90°，
∴△ACB≌△ACF（ASA），
∴FC＝BC＝6，AF＝AB＝10，
∵∠CDF＝180°﹣∠ADC，∠ABF＝180°﹣∠ADC，
∴∠CDF＝∠ABF，
∵∠CFD＝∠AFB，
∴△CFD∽△AFB，
∴＝，
∴＝，
∴AD＝．
3、如图，在Rt△ABC中，AB⊥BC，以AB为直径的圆交AC于点D，E是BC的中点，连接DE．
（1）求证：DE是⊙O的切线；
（2）设⊙O的半径为r，证明r2＝AD•OE；
（3）若DE＝4，sinC＝，求AD之长．
（1）证明：连接OD、BD，
∵AB为圆O的直径，
∴∠BDA＝90°，
∴∠BDC＝180°﹣90°＝90°，
∵E为BC的中点，
∴DE＝BC＝BE，
∴∠EBD＝∠EDB，
∵OD＝OB，
∴∠OBD＝∠ODB，
∵∠EBD+∠DBO＝90°，
∴∠EDB+∠ODB＝90°，
∴∠ODE＝90°，
∴DE是圆O的切线．
（2）证明：如图，连接BD．
由（1）知，∠ODE＝∠ADB＝90°，BD⊥AC．
∵E是BC的中点，O是AB的中点，
∴OE是△ABC的中位线，
∴OE∥AC，
∴OE⊥BD．
∴OE∥AC，
∴∠1＝∠2．
又∵∠1＝∠A，
∴∠A＝∠2．
即在△ADB与△ODE中，∠ADB＝∠ODE，∠A＝∠2，
∴△ADB∽△ODE．
∴＝，即＝．
∴r2＝AD•OE；
（3）∵AB为⊙O的直径，
∴∠ADB＝∠BDC＝90°，
∵点E为BC的中点，
∴BC＝2DE＝8，
∵sinC＝，
∴设AB＝3x，AC＝5x，
根据勾股定理得：（3x）2+82＝（5x）2，
解得x＝2．
则AC＝10．
由切割线定理可知：82＝（10﹣AD）×10，
解得，AD＝3.6．
4、如图，在△ABC中，AB＝AC，以AB为直径作⊙O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．
（1）求证：DH是⊙O的切线；
（2）若EA＝EF＝2，求⊙O的半径；
解：（1）连接OD，
∵OB＝OD，
∴∠OBD＝∠ODB，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠ODB＝∠ACB，
∴OD∥AC，
∵DH⊥AC，
∴DH⊥OD，
∴DH是⊙O的切线；
（2）设⊙O的半径为r，即OD＝OB＝r，
∵EF＝EA，
∴∠EFA＝∠EAF，
∵OD∥EC，
∴∠FOD＝∠EAF，
则∠FOD＝∠EAF＝∠EFA＝∠OFD，
∴DF＝OD＝r，
∴DE＝DF+EF＝r+2，
∴BD＝CD＝DE＝r+2，
在⊙O中，∵∠BDE＝∠EAB，
∴∠BFD＝∠EFA＝∠EAB＝∠BDE，
∴BF＝BD，△BDF是等腰三角形，
∴BF＝BD＝r+2，
∴AF＝AB﹣BF＝2OB﹣BF＝2r﹣（2+r）＝r﹣2，
∵∠BFD＝∠EFA，∠B＝∠E，
∴△BFD∽△EFA，
∴，
即＝
解得：r1＝1+，r2＝1﹣（舍），
综上所述，⊙O的半径为1+．
5、如图，B，E是⊙O上的两个定点，A为优弧BE上的动点，过点B作BC⊥AB交射线AE于点C，过点C作CF⊥BC，点D在CF上，且∠EBD＝∠A．
（1）求证：BD与⊙O相切；
（2）已知∠A＝30°．
①若BE＝3，求BD的长；
②当O，C两点间的距离最短时，判断A，B，C，D四点所组成的四边形的形状，并说明理由．
（1）证明：如图1，作直径BG，连接GE，
则∠GEB＝90°，
∴∠G+∠GBE＝90°，
∵∠A＝∠EBD，∠A＝∠G，
∴∠EBD＝∠G，
∴∠EBD+∠GBE＝90°，
∴∠GBD＝90°，
∴BD⊥OB，
∴BD与⊙O相切；
（2）解：如图2，连接AG，
∵BC⊥AB，
∴∠ABC＝90°，
由（1）知∠GBD＝90°，
∴∠GBD＝∠ABC，
∴∠GBA＝∠CBD，
又∵∠GAB＝∠DCB＝90°，
∴△BCD∽△BAG，
∴＝＝tan30°＝，
又∵Rt△BGE中，∠BGE＝30°，BE＝3，
∴BG＝2BE＝6，
∴BD＝6×＝2；
（3）解：四边形ABCD是平行四边形，理由如下，
由（2）知＝，＝，
∴＝，
∵B，E为定点，BE为定值，
∴BD为定值，D为定点，
∵∠BCD＝90°，
∴点C在以BD为直径的⊙M上运动，
∴当点C在线段OM上时，OC最小，
此时在Rt△OBM中，＝＝，
∴∠OMB＝60°，
∴MC＝MB，
∴∠MDC＝∠MCD＝30°＝∠A，
∵AB⊥BC，CD⊥BC，
∴∠ABC＝∠DCB＝90°，
∴AB∥CD，
∴∠A+∠ACD＝180°，
∴∠BDC+∠ACD＝180°，
∴AC∥BD，
∴四边形ABCD为平行四边形．
6、如图，AB、CE是⊙O的直径，过点C的切线与AB的延长线交于点P，AD⊥PC于D，连接AC、OD、PE．
（1）求证：AC是∠DAP的角平分线；
（2）求证：PC2＝PA•PB；
（3）若AD＝3，PE＝2DO，求⊙O的半径．
证明：（1）∵PC是圆的切线，AD⊥PD，
∴AD∥OC，
∴∠DAC＝∠ACO，
∵AO＝CO，
∴∠CAO＝∠ACO，
∴∠DAC＝∠CAO，
∴AC是∠DAP的平分线；
（2）如右图，连接BC，
∵OC＝OB，
∴∠OCB＝∠OBC，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠CAB+∠OBC＝90°，
∵PC是⊙O的切线，
∴∠OCB+∠BCP＝90°，
∴∠CAB＝∠BCP，
又∵∠CPB＝∠APC，
∴△CPB∽△APC，
∴＝，
∴PC2＝PA•PB；
（3）设半径为r，在Rt△PCE中，PE2＝（2r）2+PC2＝4r2+PC2，
∵PE＝2DO，
∴4DO2＝4r2+PC2，
∴4（DO2﹣r2）＝PC2，
∴4DC2＝PC2，
∴PC＝2CD，
∵AD∥OC，
∴△PCO∽△PDA，
∴＝，
∴＝，
∴r＝2．
7、如图，AB是直经，D是的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于点F．
（1）求证：DE是⊙O的切线．
（2）试探究AE，AD，AB三者之间的等量关系．
（3）若DE＝3，⊙O的半径为5，求BF的长．
（1）证明：如图1，连接OC，OD，BC，
∵AB是直径，
∴∠ACB＝90°，
∵DE⊥AC于E，
∴∠E＝90°，
∴∠ACB＝∠E，
∴BC∥DE，
∵点D是的中点，
∴，
∴∠COD＝∠BOD，
又∵OC＝OB，
∴OD垂直平分BC，
∵BC∥DE，
∴OD⊥DE，
∴DE是⊙O的切线；
（2）AD2＝AE•AB，理由如下：
如图2，连接BD，
由（1）知，，
∴∠EAD＝∠DAB，
∵AB为直径，
∴∠ADB＝∠E＝90°，
∴△AED∽△ADB，
∴＝，
即AD2＝AE•AB；
（3）由（1）知，∠E＝∠ECH＝∠CHD＝90°，
∴四边形CHDE为矩形，
∴ED＝CH＝BH＝3，
∴OH＝＝＝4，
∴CE＝HD＝OD﹣OH＝5﹣4＝1，AC＝＝＝8，
∴AE＝AC+CE＝9，
∵BF是⊙O的切线，
∴∠FBA＝∠E＝90°，
又∵∠EAD＝∠DAB，
∴△EAD∽△BAF，
∴＝，
即＝，
∴BF＝．
8、已知正方形ABCD内接于⊙O，点E为上一点，连接BE、CE、DE．
（1）如图1，求证：∠DEC+∠BEC＝180°；
（2）如图2，过点C作CF⊥CE交BE于点F，连接AF，M为AE的中点，连接DM并延长交AF于点N，求证：DN⊥AF；
（3）如图3，在（2）的条件下，连接OM，若AB＝10，tan∠DCE＝，求OM的长．
（1）证明：连接BD，OC，
∵四边形ABCD为正方形，
∴∠A＝90°，BC＝CD，
∴BD为⊙O的直径，
∵OB＝OD，
∴OC⊥BD，
∴∠BOC＝90°，
∴∠BEC＝∠BOC＝45°，
∵正方形ABED是圆O的内接四边形，
∴∠A+∠DEB＝180°，
∴∠DEB＝90°，
∴∠DEC+∠BEC＝∠DEB+∠BEC+∠BEC＝180°；
（2）证明：如图2，延长ED至G，使ED＝DG，连接AG，
∵CE⊥CF，
∴∠ECF＝90°，
∵∠CEF＝45°，
∴∠CEF＝∠CFE＝45°，
∴CE＝CF，
∵∠BCD＝∠ECF＝90°，
∴∠BCF＝∠DCF，
∵BC＝CD，
∴△BFC≌△DEC（SAS），
∴BF＝DE，
∵DE＝DG，
∴BF＝DG，
∵四边形ABED为圆O的内接四边形，
∴∠ABE+∠ADE＝180°，
∵∠ADE+∠ADG＝180°，
∴∠ABE＝∠ADG，
∵AB＝AD，
∴△ABF≌△ADG（SAS），
∴∠BAF＝∠DAC，
∵∠BAF+∠FAD＝∠BAD＝90°，
∴∠DAG+∠FAD＝90°，
∴∠FAG＝90°，
∵M为AE的中点，
∴DM为△AEG的中位线，
∴DM∥AG，
∴∠DNF＝∠FAG＝90°，
∴DN⊥AF，
（3）解：如图3，连接BD，OC，过点B作BK⊥CF交CF的延长线于点K，过点B作BT⊥AE于点T，
由（1）知∠BOC＝90°，
∴OB＝OC＝，
由（1）知BD为⊙O的直径，在Rt△ABD中，BD＝AB＝10，
∵，
∴∠DBE＝∠DCE，
∴tan∠DCE＝tan∠DBE＝，
∴，设DE＝x，则BE＝7x，
在Rt△BDE中，BD＝＝5x，
∴，
∴x＝2，
∴DE＝2，
∴BF＝2，
∵∠EFC＝45°，
∴∠BFK＝∠EFC＝45°，
∴∠KBF＝∠BFK＝45°，
∴，
由（2）知∠BCF＝∠DCE，
∴tan∠BCF＝tan∠DCE＝，
∴，
∴，
∴，
在Rt△ECF中，EF＝CF＝12，
∴BE＝EF+BF＝14，
∵∠AEB＝∠AEC﹣∠BEC＝90°﹣45°＝45°，
∴∠TBE＝∠TEB，
∴TB＝TE＝，
∴＝，
∴，
∴，
∵M为AE的中点，
∴OM⊥AE，
在Rt△OME中，OM＝＝3．
9、已知：在⊙O中，弦AC⊥弦BD，垂足为H，连接BC，过点D作DE⊥BC于点E，DE交AC于点F．
（1）如图1，求证：BD平分∠ADF；
（2）如图2，连接OC，若AC＝BC，求证：OC平分∠ACB；
（3）如图3，在（2）的条件下，连接AB，过点D作DN∥AC交⊙O于点N，若AB＝3，DN＝9．求sin∠ADB的值．
（1）证明：如图1，
∵AC⊥BD，DE⊥BC，
∴∠AHD＝∠BED＝90°，
∴∠DAH+∠ADH＝90°，∠DBE+∠BDE＝90°，
∵∠DAC＝∠DBC，
∴∠ADH＝∠BDE，
∴BD平分∠ADF．
（2）证明：连接OA、OB．
∵OB＝OC＝OA，AC＝BC
∴△OCB≌△OCA（SSS），
∴OBC＝∠OCA，
∴OC平分∠ACB；
（3）如图3中，连接BN，过点O作OP⊥BD于点P，过点O作OQ⊥AC于点Q．
则四边形OPHQ是矩形，
∵DN∥AC，
∴∠BDN＝∠BHC＝90°，
∴BN是直径，
则OP＝DN＝，
∴HQ＝OP＝，
设AH＝x，则AQ＝x+，AC＝2AQ＝2x+9，BC＝AC＝2x+9，
∴CH＝AC﹣AH＝2x+9﹣x＝x+9
在Rt△AHB中，BH2＝AB2﹣AH2＝（）2﹣x2．
在Rt△BCH中，BC2＝BH2+CH2，
即（2x+9）2＝（）2﹣x2+（x+9）2，
整理得2x2+9x﹣45＝0，
（x﹣3）（2x+15）＝0
解得 x＝3（负值舍去），
BC＝2x+9＝15，CH＝x+9＝12
∵∠ADB＝∠BCH，
∴sin∠ADB＝sin∠BCH＝＝＝．
即sin∠ADB的值为．
10、如图，已知AB为⊙O的直径，AD、BD是⊙O的弦，BC是⊙O的切线，切点为B，OC∥AD，BA、CD的延长线相交于点E．
（1）求证：DC是⊙O的切线；
（2）若AE＝1，ED＝3，求⊙O的半径．
（3）在（2）中的条件下，∠ABD＝30°，将△ABD以点A为中心逆时针旋转120°，求BD扫过的图形的面积（结果用π表示）．
证明：（1）连接DO，如图，
∵AD∥OC，
∴∠DAO＝∠COB，∠ADO＝∠COD，
又∵OA＝OD，
∴∠DAO＝∠ADO，
∴∠COD＝∠COB．
在△COD和△COB中
∴△COD≌△COB（SAS），
∴∠CDO＝∠CBO．
∵BC是⊙O的切线，
∴∠CBO＝90°，
∴∠CDO＝90°，
∴OD⊥CE，
又∵点D在⊙O上，
∴CD是⊙O的切线；
（2）设圆O的半径为R，
则OD＝R，OE＝R+1，
∵CD是圆O的切线，
∴∠EDO＝90°，
∴ED2+OD2＝OE2，
∴9+R2＝（R+1）2，
∴R＝4，
∴圆O的半径为4；
（3）∵∠ABD＝30°，AB＝2R＝8，
∴AD＝4，
∴BD扫过的图形的面积＝＝16π．
11、如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，连结OA、OB、OC，延长BO与AC交于点D，与⊙O交于点F，延长BA到点G，使得∠BGF＝∠GBC，连接FG．
（1）求证：FG是⊙O的切线；
（2）若⊙O的径为4．
①当OD＝3，求AD的长度；
②当△OCD是直角三角形时，求△ABC的面积．
（1）证明：连接AF，
∵BF为⊙O的直径，
∴∠BAF＝90°，∠FAG＝90°，
∴∠BGF+∠AFG＝90°，
∵AB＝AC，
∴∠ABC＝∠ACB，
∵∠ACB＝∠AFB，∠BGF＝∠ABC，
∴∠BGF＝∠AFB，
∴∠AFB+∠AFG＝90°，即∠OFG＝90°，
又∵OF为半径，
∴FG是⊙O的切线；
（2）解：①连接CF，则∠ACF＝∠ABF，
∵AB＝AC，AO＝AO，BO＝CO，
∴△ABO≌△ACO（SSS），
∴∠ABO＝∠BAO＝∠CAO＝∠ACO，
∴∠CAO＝∠ACF，
∴AO∥CF，
∴＝，
∵半径是4，OD＝3，
∴DF＝1，BD＝7，
∴＝＝3，即CD＝AD，
∵∠ABD＝∠FCD，∠ADB＝∠FDC，
∴△ADB∽△FDC，
∴＝，
∴AD•CD＝BD•DF，
∴AD•CD＝7，即AD2＝7，
∴AD＝（取正值）；
②∵△ODC为直角三角形，∠DCO不可能等于90°，
∴存在∠ODC＝90°或∠COD＝90°，
当∠ODC＝90°时，
∵∠ACO＝∠ACF，
∴OD＝DF＝2，BD＝6，
∴AD＝CD，
∴AD•CD＝AD2＝12，
∴AD＝2，AC＝4，
∴S△ABC＝×4×6＝12；
当∠COD＝90°时，
∵OB＝OC＝4，
∴△OBC是等腰直角三角形，
∴BC＝4，
延长AO交BC于点M，
则AM⊥BC，
∴MO＝2，
∴AM＝4+2，
∴S△ABC＝×4×（4+2）＝8+8，
∴△ABC的面积为12或8+8．