专题01 全等三角形中的辅助线做法及常见题型-2022届中考数学压轴大题专项训练

这是一份专题01 全等三角形中的辅助线做法及常见题型-2022届中考数学压轴大题专项训练，文件包含专题01全等三角形中的辅助线做法及常见题型解析版docx、专题01全等三角形中的辅助线做法及常见题型原卷版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
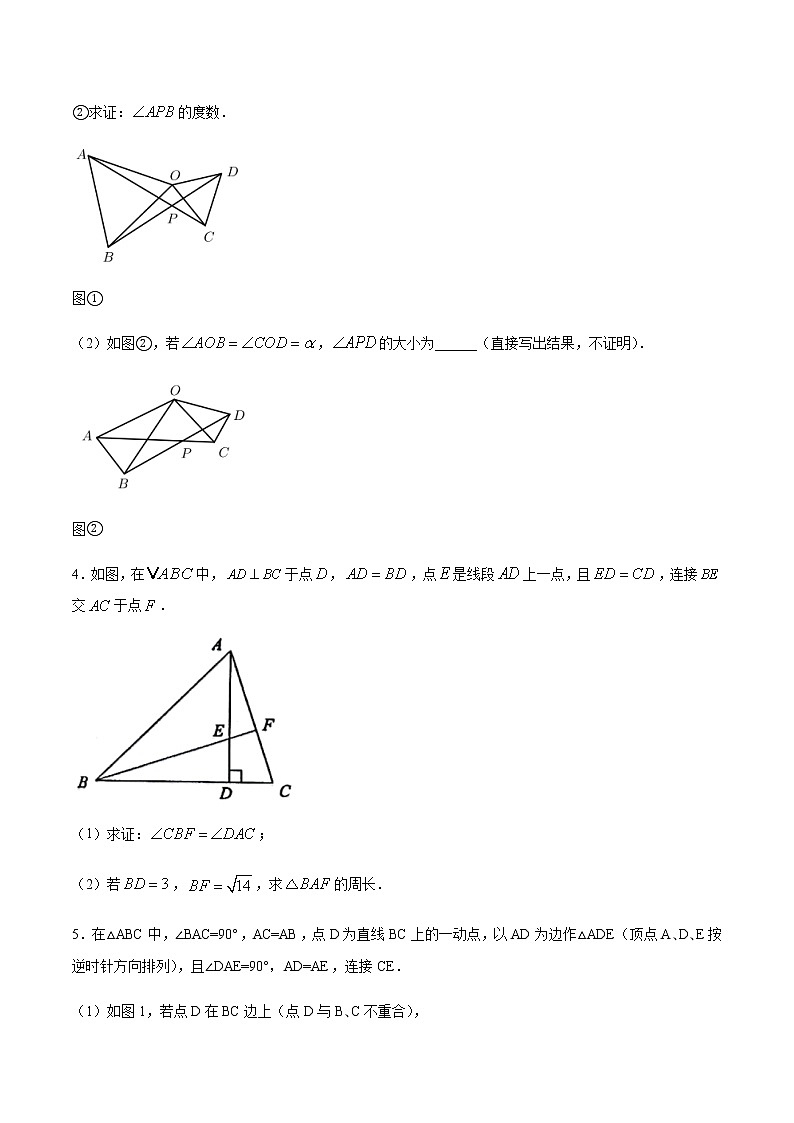
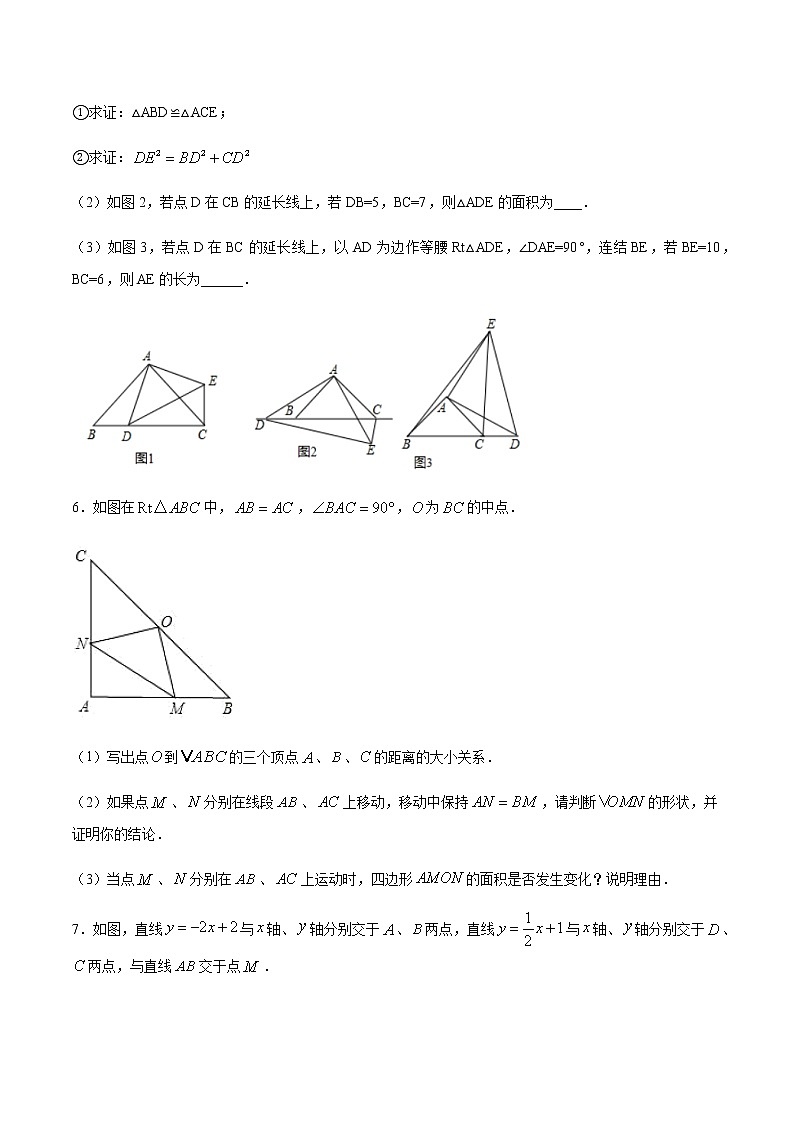
专题01  全等三角形中的辅助线做法及常见题型  2021届中考数学压轴大题专项训练(原卷版)1．如图，在中，，．是的中点，且，点在上，点在上（1）求证：；（2）若，求四边形的面积．2．如图，中，点D在边上，且．   （1）求证：；（2）点E在边上，连接交于点F，且，，求的度数．（3）在（2）的条件下，若，的周长等于30，求的长．3．已知：在和中，，．（1）如图①，若①求证：．②求证：的度数．图①（2）如图②，若，的大小为______（直接写出结果，不证明）．图②4．如图，在中，于点，，点是线段上一点，且，连接交于点．（1）求证：；（2）若，，求的周长．5．在△ABC中，∠BAC=90°，AC=AB，点D为直线BC上的一动点，以AD为边作△ADE（顶点A､D､E按逆时针方向排列），且∠DAE=90°，AD=AE，连接CE．（1）如图1，若点D在BC边上（点D与B､C不重合），①求证：△ABD≌△ACE；②求证：（2）如图2，若点D在CB的延长线上，若DB=5，BC=7，则△ADE的面积为____．（3）如图3，若点D在BC的延长线上，以AD为边作等腰Rt△ADE，∠DAE=90°，连结BE，若BE=10，BC=6，则AE的长为______．6．如图在中，，，为的中点．（1）写出点到的三个顶点、、的距离的大小关系．（2）如果点、分别在线段、上移动，移动中保持，请判断的形状，并证明你的结论．（3）当点、分别在、上运动时，四边形的面积是否发生变化？说明理由．7．如图，直线与轴、轴分别交于、两点，直线与轴、轴分别交于、两点，与直线交于点．（1）填空：点的坐标是（________，________），点的坐标是（________，________）；（2）直线与直线的位置关系________；（3）线段的长为________；（4）在第一象限是否存在点，使得是等腰直角三角形，请直接写出所有满足条件的点的坐标________．8．如图1，两个不全等的等腰直角三角形和叠放在一起，并且有公共的直角顶点．将图1中的绕点顺时针旋转，在图2中作出旋转后的△OAB(保留作图痕迹，不写作法，不证明)；在图1中，你发现线段的数量关系是____，直线 相交成         角(填“锐”、“钝”或“直”)；①将图1中的绕点顺时针旋转一个锐角， 得到图，这时(2)中的两个结论是否仍成立?作出判断并说明理由； ②若将绕点继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．9．问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于，那么它所对的直角边等于斜边的一半．即：如图（1），在中，，，则．探究结论：小明同学对以上结论作了进一步研究．（1）如图（1），作边上的中线，得到结论：①为等边三角形；②与之间的数量关系为_________．（2）如图（2），是的中线，点D是边上任意一点，连接，作等边，且点P在的内部，连接．试探究线段与之间的数量关系，写出你的猜想并加以证明．（3）当点D为边延长线上任意一点时，在（2）中条件的基础上，线段与之间存在怎样的数量关系？直接写出答案即可．10．如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想：图1中，线段PM与PN的数量关系是　   ，位置关系是　   ；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．11．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E(1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；(2)当直线MN绕点C旋转到图2的位置时，直接写出DE、AD、BE的关系为：___；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系，并加以证明．12．（1）（方法探索）如图，在等边中，点在内，且，，，求的长．小敏在解决这个问题时，想到了以下思路：如图，把绕着点顺时针旋转得到，连接，分别证明和是特殊三角形，从而得解．请在此思路提示下，求出PB的长．解：把绕着点顺时针旋转得到，连接，请接着写下去：（2）（方法应用）请借鉴上述利用旋转构图的方法，解决下面问题①如图，点在等边外，且，，，若，求度数；②如图，在中，，，是外一点，连接、、已知，．请直接写出的长．