2022年中考数学二次函数压轴300题终极突破提升训练（12）

这是一份2022年中考数学二次函数压轴300题终极突破提升训练（12），文件包含中考数学二次函数压轴300题终极突破提升训练12解析版doc、中考数学二次函数压轴300题终极突破提升训练12原卷版doc等2份试卷配套教学资源，其中试卷共47页， 欢迎下载使用。
中考数学二次函数压轴300题终极突破提升训练（12）

1．如图，抛物线交轴于，交轴于，直线平行于轴，与抛物线另一个交点为．

（1）求抛物线的函数表达式及点D的坐标；
（2）若抛物线与抛物线关于轴对称，是轴上的动点，在抛物线上是否存在一点，使得以为顶点且为边的四边形是平行四边形，若存在，请求出点的坐标，若不存在，请说明理由.
【答案】（1）；（2，3）（2）存在；(或(或或
【分析】（1）利用点A，B的坐标设抛物线的交点式解析式，再将点C代入即可求解，再令，即可求出D点坐标；
（2）先求出抛物线的解析式，再过点作轴于点，过点作轴于点，根据平行四边形的性质可得，进而证明得到，故可求出N点坐标．
【详解】解：(1)令，则，∴．
设抛物线的函数表达式，
将点代人，
得，，
解得，，
∴抛物线的函数表达式为．
令，即，解得
．
(2)∵抛物线与抛物线关于轴对称，
又，
∴抛物线的函数表达式为．
过点作轴于点，过点作轴于点，
当以为顶点且为边的四边形是平行四边形时，，
∴∠DBE=∠NMF，
又∠DEB=∠NFM=90°
∴
，即．
①当时，
解得，
∴，
②当时，
解得，
∴．

综上，满足条件的点的坐标为(或(或或．
【点评】本题考查了待定系数法法求二次函数解析式，平行四边形的性质及平移规律等，解题关键是能够灵活运用平行四边形的性质及平移规律等．
2．如图，已知抛物线 （ 为常数）经过点 ，与 轴相 交于点 、（点 在点 的右侧）．
（1）求抛物线的解析式和点 的坐标；
（2）将直线 向下平移 （ ）个单位长度后，得到的直线与抛物线只有一个公共点 ，求点 的坐标；
（3）在（2）的条件下，连接 、，在 正半轴上是否存在点 ，使以 、、 为顶点的三角形与 相似.若存在，请求出点 的坐标；若不存在，请说明理由．

【答案】（1）y=x2﹣3x，点B的坐标为（3，0）；（2）（2，﹣2）；（3）存在，点P的坐标为（，0）或（6，0）
【分析】（1）将代入中得出b的值，从而确定抛物线的解析式，再令得出点B 的坐标；
（2）根据待定系数法得出直线OA的解析式y=x，再设出平移后的解析式y=x﹣m，与二次函数解析式组成方程组，再根据△=16﹣4m=0，求出m的值，从而确定 的坐标；
（3）根据A、D两点坐标得出OA和OD的长，再分△OAP∽△OBD和△OAP∽△ODB两种情况进行讨论即可．
【详解】解：（1）∵抛物线y=x2+bx经过A（4，4），
∴将A点坐标代入得：，解得：，
∴抛物线的解析式是y=x2﹣3x．
令，得：，解得：，.
∴点B的坐标为（3，0）.
（2）设直线OA的解析式为y=k1x，由点A（4，4），
得：4=4k1，解得：k1=1 ，
∴直线OA的解析式为y=x，
∴直线OA向下平移m个单位长度后的解析式为：
y=x﹣m，
∴x﹣m=x2﹣3x，
∵抛物线与直线只有一个公共点，∴△=16﹣4m=0，
解得：m=4，
此时x1=x2=2，y=x2﹣3x=﹣2，
∴D点的坐标为（2，﹣2）．
（3）由点A（4，4）可得，∠AOB=45°,
由点D（2，—2）可得，∠DOB=45°,
∴∠AOB=∠DOB.
，
.
如图，当∠OAP=∠OBD时，△OAP∽△OBD,
则，.
∴ ，∴OP=.
‚如图‚，当∠OAP=∠ODB时，△OAP∽△ODB,
则，，即，
∴ OP=6
故点P的坐标为（，0）或（6，0）．
【点评】本题是二次函数的综合题，涉及到待定系数法、二次函数与方程组以及相似三角形的性质等，熟练掌握相关的知识点是解题的关键．
3．如图，已知二次函数y＝ax2＋bx＋4的图象与x轴交于点B(－2，0)、点C(8，0)两点，与y轴交于点A．
(1)求二次函数的表达式；
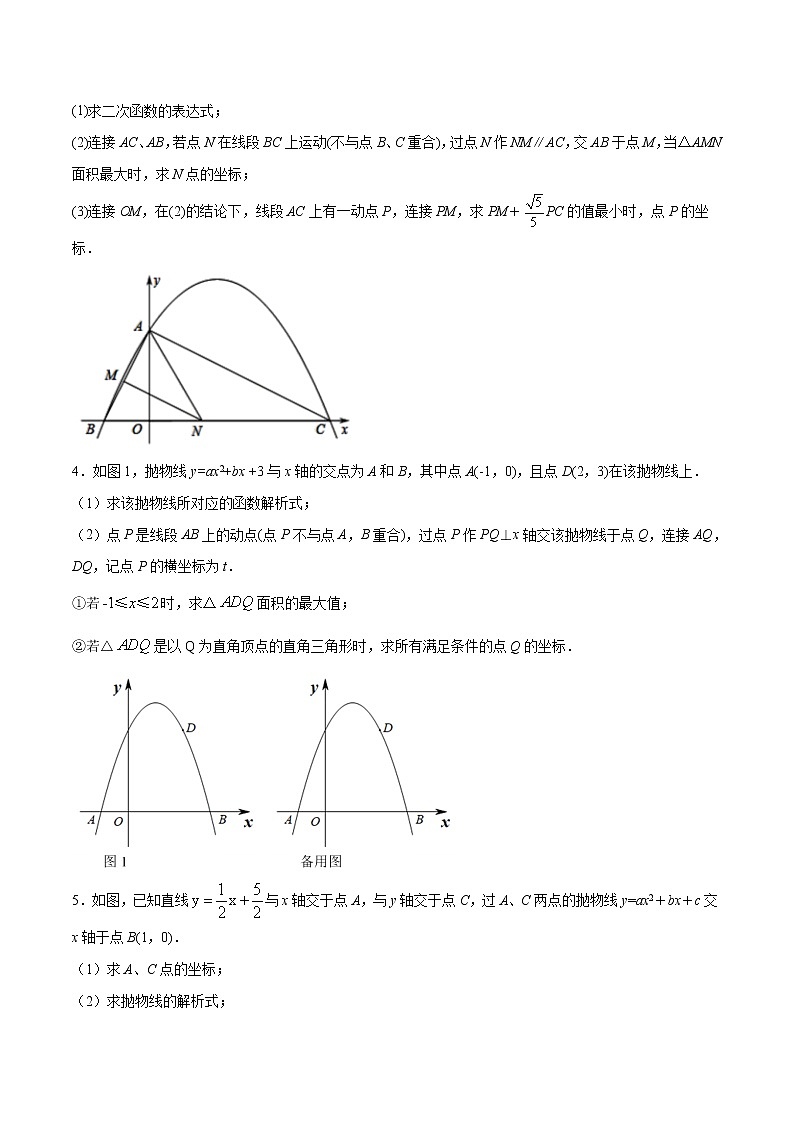
(2)连接AC、AB，若点N在线段BC上运动(不与点B、C重合)，过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；
(3)连接OM，在(2)的结论下，线段AC上有一动点P，连接PM，求PM＋PC的值最小时，点P的坐标．

【答案】（1）y=﹣x2+x+4；(2) N（3，0）； (3) P(1，) ．
【分析】（1）由B、C的坐标，利用待定系数法可求得抛物线解析式；
（2）可设N（n，0），则可用n表示出△ABN的面积，由NM∥AC，可求得，则可用n表示出△AMN的面积，再利用二次函数的性质可求得其面积最大时n的值，即可求得N点的坐标；
（3）过点PD⊥x轴于点D，点E为M关于AC的对称点，作EF⊥x轴于点F，则PM＋PC的最小值即为EF的长．求出直线AC的解析式，并证明,再由（2）知，利用中点公式可得E的坐标，再将点E的横坐标代入直线AC，从而得解．
【详解】（1）将点B，点C的坐标分别代入y=ax2+bx+4可得，

解得，
∴二次函数的表达式为y=﹣x2+x+4；
（2）设点N的坐标为（n，0）（﹣2＜n＜8），则BN=n+2，CN=8﹣n．
∵B（﹣2，0），C（8，0），
∴BC=10，
在y=﹣x2+x+4中，令x=0，可解得y=4，
∴点A（0，4），OA=4，
∴S△ABN=BN•OA=（n+2）×4=2（n+2），
∵MN∥AC，
∴
∴
∴
∵﹣＜0，
∴当n=3时，即N（3，0）时，△AMN的面积最大；
（3）如图，过点PD⊥x轴于点D，点E为M关于AC的对称点，作EF⊥x轴于点F，

,易得，当E、P、D三点共线时，可知PM＋PC的最小值即为EF的长．
由（2）可得M(-1,2),
由A(0,4)，B(-2,0),C(8,0),得直线AC:
在中，，
，

即是直角三角形，且,
∵M,E关于AC对称，
∴A（0，4）是ME的中点，由中点坐标公式得，
∴点P横坐标是1，代入，得y=,
则P(1，) ．
【点评】本题为二次函数的综合应用，涉及待定系数法、平行线分线段成比例、三角形的面积、二次函数的性质、直角三角形的性质、勾股定理等知识．
4．如图1，抛物线y=ax2+bx +3与x轴的交点为A和B，其中点A(-1，0)，且点D(2，3)在该抛物线上．
（1）求该抛物线所对应的函数解析式；
（2）点P是线段AB上的动点(点P不与点A，B重合)，过点P作PQ⊥x轴交该抛物线于点Q，连接AQ，DQ，记点P的横坐标为t．
①若时，求△面积的最大值；
②若△是以Q为直角顶点的直角三角形时，求所有满足条件的点Q的坐标．

【答案】（1）；（2）①当时，△ADQ面积最大为；②Q（，）或（，）．
【分析】（1）把A(-1,0），D（2，3）代入解析式即可求解；
（2）①由P的横坐标为t， Q（t，）,求出直线AD的解析式为，设点C为直线PQ与直线AD的交点，求得点坐标为（），得到，利用，将△面积表示为关于t的二次函数，故可求解；
②△AQD是以Q为直角顶点的直角三角形时,∠AQD=90°，过点D作DK⊥PQ于点K，
证明△PQA∽△KDQ得到，代入得，解出t即可求解．
【详解】（1）解：将A(-1,0）和点D（2，3）代入得，
，
解得，
∴该抛物线的解析式为．
（2）①由P的横坐标为t，则P（t，0），Q（t，）．
设直线AD的解析式为y=kx+b（k≠0）
把A（-1，0），D（2，3）代入得
解得
∴直线AD的解析式为
如图：设点C为直线PQ与直线AD的交点
当时，
∴点坐标为（）
∴

∴




抛物线开口向下
∴当时，△ADQ面积最大为；
②△AQD是以Q为直角顶点的直角三角形时,∠AQD=90°，
过点D作DK⊥PQ于点K，
∴∠APQ=∠QKD=90°，
∵∠DQK+∠PQA=90°，
又∠DQK+∠KDQ=90°，
∴∠PQA=∠KDQ，
∴△PQA∽△KDQ
∴，
∴，
∴，
∵，（即Q不与A、D重合），
∴，整理得：，
解得，
经验证，、均符合题意，
其中：，符合图a的情况，，符合图b的情况．
当时，；当时，，
∴Q（，）或（，）．

【点评】此题主要考查二次函数综合，解题的关键是熟知待定系数法、二次函数的最值及相似三角形的判定与性质．
5．如图，已知直线与x轴交于点A，与y轴交于点C，过A、C两点的抛物线y=ax2＋bx＋c交x轴于点B(1，0)．
（1）求A、C点的坐标；
（2）求抛物线的解析式；
（3）在直线AC上方的抛物线上是否存在点E，使得∠ECA=2∠CAB，若存在这样的点E，求出△ACE的面积；若不存在，请说明理由．

【答案】（1）A(－5，0)，C(0，)；（2） ；（3）存在，．
【分析】（1）分别代入x=0，y=0即可求得；
（2）待定系数法即可求得抛物线解析式；
（3）过点C作CM∥AB，过点E作EF⊥CM，证△CEF∽△ACO，得，设点E（m，)，根据比例关系即可求得.
【详解】解：（1）当y=0时，x＋=0，
解得：x=－5，则A(－5，0)；
当x=0时，y=，
∴C点坐标为（0，）；
（2）设抛物线的解析式为y=ax2＋bx＋c，代入A，B，C三点，
，解得 ，
∴抛物线的解析式为：；
（3）存在．如图，过点C作CM∥AB，过点E作EF⊥CM，

∴∠MCA=∠CAB．
∵∠ECA=2∠CAB=∠ECF＋∠MCA，
∴∠ECF=∠CAB．
∵∠AOC=∠EFC=90°，
∴△CEF∽△ACO，
∴．
设点E（m，)，OC=，
∴，
解得：m=－3或m=0(不合题意，舍去)，
∴点E(－3，4)
∴S△ACE=×(3＋5)×4－××3-×5×=．
【点评】本题为二次函数综合题，结合一次函数主要考查用待定系数法求抛物线的解析式、抛物线上点的坐标特征、相似三角形的判定与性质，有一定的综合性，熟练掌握抛物线性质是解题的关键.
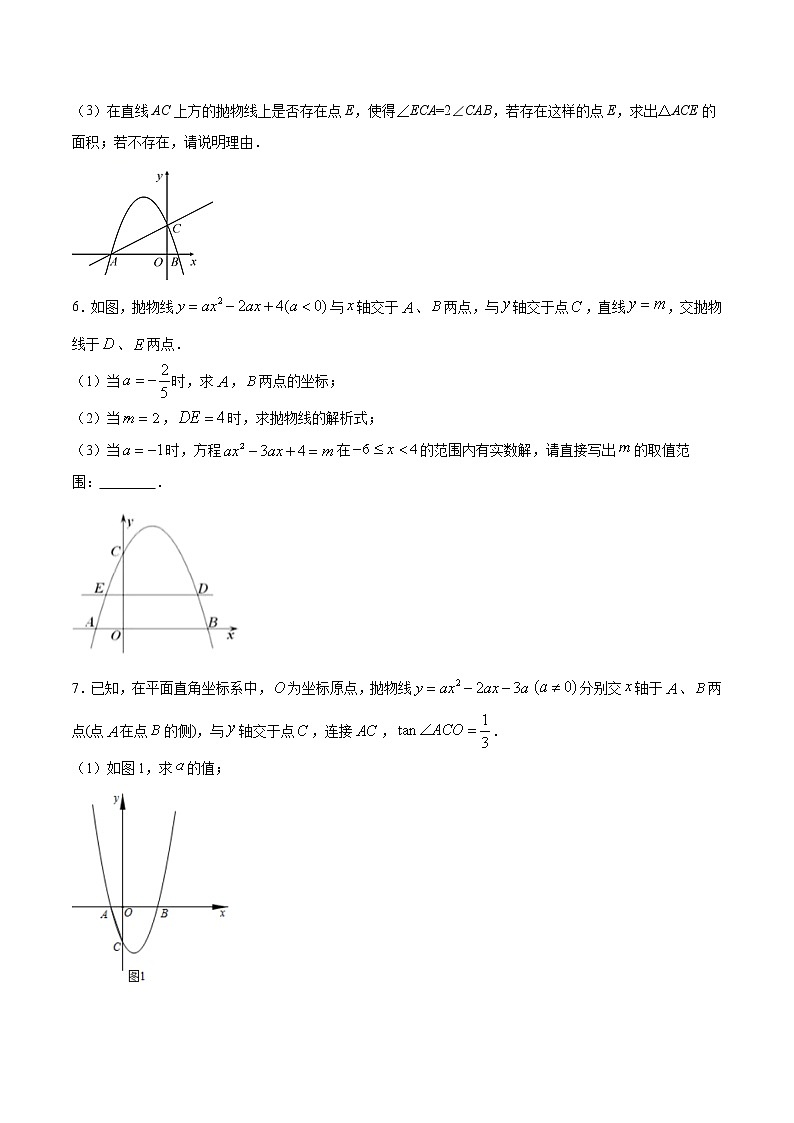
6．如图，抛物线与轴交于、两点，与轴交于点，直线，交抛物线于、两点．
（1）当时，求，两点的坐标；
（2）当，时，求抛物线的解析式；
（3）当时，方程在的范围内有实数解，请直接写出的取值范围：　　　　．

【答案】（1），；（2）；（3）-．
【分析】(1)将代回中，再令y=0即可求解;
(2)求出抛物线的对称轴，再由DE=4进而求出点D的坐标，再代回抛物线中即可求解.
(3)将代回方程中，将方程左边可以看成二次函数，方程右边可以看成，求出在的范围内的最大值和最小值即可求解.
【详解】解：(1)将代回中
得到抛物线的解析式为：
再令，即：
解得
故，.
故答案为：，.
(2)对称轴是直线
∵，，
∴，代入解析式中：
解得
∴抛物线的解析式为：.
故答案为：.
(3) 当时，方程
方程左边可以看成二次函数，
方程右边可以看成，
∵方程在的范围内有实数解
∴函数和直线在的范围内图像上有交点，
∴当时，
函数的最大值为当时取得，此时；
函数的最小值为当时取得，此时；
故的取值范围是：-.
故答案为：.
【点评】本题利用数形结合，根据二次函数性质理解其本质，主要是二次函数图象的轴对称性、增减性、在自变量范围内求函数的最值，熟练记住二次函数的三种表达式、对称轴、顶点公式是解决这类题的关键．
7．已知，在平面直角坐标系中，为坐标原点，抛物线分别交轴于、两点(点在点的侧)，与轴交于点，连接，．
（1）如图1，求的值；

（2）如图2，是轴上一点(不与点、重合)，过点作轴的平行线，交抛物线于点，交直线于点．

①当点在点右侧时，连接AF，当时，求的长．
②当点在运动时，若、、中有两条线段相等，此时点的坐标_________．

【答案】（1）；（2）①；②的坐标为，．
【分析】（1）由ax²−2ax−3a＝0，可得A（−1，0），B（3，0），OA＝1，再根据tan∠ACO＝，可求得C（0，−3），即可求出a的值；
（2）①构造全等三角形，由此AD＝ED，设，建立方程求解；
②分两种情况讨论，分别建立方程进行求解即可得到答案.
【详解】（1）
令，即，解得，，
∴，，
∴，
又∵，
∴；
（2）①由（1）得抛物线，BC所在直线，
设，
∴，
∵，轴，
∴为等腰直角三角形，
又∵，
∴，
∴而，
∴，
∴，，
∴，
∴
②当

，
∴，∴
当
，
∴，即，
∴，
∴D（-2，0），
综上，的坐标为，
【点评】本题考查了二次函数的综合，求抛物线解析式，运用三角函数解直角三角形及勾股定理，全等三角形性质与判定等，关键要善于利用题目中条件构造直角三角形，运用勾股定理和解直角三角形知识解题．
8．如图，一次函数分别交轴、轴于两点，抛物线过两点

（1）求抛物线的解析式；
（2）作直线垂直于轴，在第一象限交直线于点，交抛物线于点，交轴于点．求当取何值时，有最大值？最大值是多少？
（3）在（2）的情况下，以为顶点作平行四边形，请直接写出第四个顶点的坐标．
【答案】（1）；（2）当时，有最大值，最大值是；（3）或
【分析】（1）先求出点A、B的坐标，再利用待定系数法求解；
（2）根据点M、N所在的函数解析式得到点M及N的坐标，计算，并化为顶点式形式，根据函数的性质解答；
（3）先确定M（2,1），N（2,5），设点D的坐标为（m，n），分三种情况，①当MD为对角，②当AM为对角线时，③当MN为对角线时，根据直角坐标系中平行四边形的点坐标的性质解答．
【详解】（1）令中y=0，得，解得x=4，
令中x=0，得y=2，
点的坐标为，
将点A、B的坐标代入中，得
，
解得，
抛物线解析式为；
轴于点，且点，

点在直线上，点在抛物线上，
，




当时，有最大值，最大值是；
(3）∵t=2，
∴M（2,1），N（2,5），
设点D的坐标为（m，n），
∵以为顶点作平行四边形，
∴①当MD为对角线时，m+2=0+2，n+1=2+5，
解得m=0，n=6，
∴D（0,6）；
②当AM为对角线时，m+2=0+2，n+5=2+1，
解得m=0，n=-2，
∴D（0，-2）；
③当MN为对角线时，m+0=2+2，n+2=1+5，
解得m=4，n=4，
∴D（4,4），
综上，所求的点坐标为或．
【点评】此题考查待定系数法求函数解析式，函数图象与坐标轴的交点，二次函数与最值问题，直角坐标系中平行四边形对角顶点的横坐标的和相等，纵坐标的和相等，（3）根据平行四边形的性质解答更为简便，同时运用分类思想解决问题．
9．如图，在平面直角坐标系中，为坐标原点，为等腰底边上的高，直线的解析式为，抛物线的顶点为点，且经过坐标原点．

（1）求该抛物线的解析式；
（2）有一动点从点出发，沿射线方向以每秒个单位长度的速度运动，连接，设的面积为，点的运动时间为秒，求与的关系式，并直接写出自变量的取值范围；
（3）在（2）的条件下，过点做的垂线交射线于点，过点作的垂线交抛物线于点，直接写出当为何值时，的长为，并写出此时点的坐标．
【答案】（1）；（2）或；（3）时，点F为，时，点F为．
【分析】（1）由抛物线的解析式可求得抛物线的对称轴为x=4，根据点A在y=x上可求得点A的坐标为（4，4），将（4，4），（0，0）代入抛物线的解析式可求得a和k的值，从而得到抛物线的解析式；
（2）当点P在线段OA上时，如图1所示，过点P作PM⊥AD于点M．在等腰三角形APM中，利用特殊锐角三角函数值可求得，然后利用三角形的面积公式即可求得S与t的关系式，如图2所示，先求得，然后利用三角形的面积公式即可求得S与t的关系式；
（3）在图3中先证明△PAD≌△ECD，，由PA=AO-OP可得：，解得：，设EF交x轴于点N，在Rt△CEN中，∠ECN=45°，，于是CN=1，故此ON=7，将x=7代入抛物线的解析式可求得点F的坐标；在图4中同理计算即可．
【详解】（1）抛物线的顶点为点，
点的横坐标为，
直线的解析式为，
当时，，
点的坐标为．
将，代入得，解得，
抛物线的解析式为；
（2）①当点在线段上时，如图1，过点作于点，
为等腰底边上的高，且点坐标为，
，
，
，
，
，
此时的取值范围是：，

②当点在线段的延长线上时，如图2，，
，
此时的取值范围是：；

综上，S=8-2t(0