2022年中考数学二次函数压轴300题终极突破提升训练（20）

这是一份2022年中考数学二次函数压轴300题终极突破提升训练（20），文件包含中考数学二次函数压轴300题终极突破提升训练20解析版doc、中考数学二次函数压轴300题终极突破提升训练20原卷版doc等2份试卷配套教学资源，其中试卷共50页， 欢迎下载使用。
中考数学二次函数压轴300题终极突破提升训练（20）

1．如图，在平面直角坐标系中，抛物线与轴交于两点(点在点的左侧)，经过点的直线与轴负半轴交于点与抛物线的另一个交点为，且点的横坐标为．
(1)直接写出点的坐标，并求直线的函数表达式(其中用含的式子表示)；
(2)点是直线上方的抛物线上的动点，若的面积的最大值为，求抛物线的解析式；
(3)在(2)的条件下，求四边形的面积．


【答案】(1)A(-1，0)，()；(2)；(3)
【分析】(1)通过解方程得到点A的横坐标；把点D的横坐标代入二次函数解析式得到，由此求得，结合点A、D的坐标来求直线的函数表达式；
(2)过点E作EF∥y轴，交直线l于点F，由函数图象上点的坐标特征可以设设E(，)，则F(，)，结合图形得到：S△ACE =S△AFE - S△CFE= ( )2，根据二次函数的最值求得答案；
(3)求得点E的坐标为(，)，点D的坐标为(，)，利用S四边形CDBE=S四边形ADBE- S△ACE=S△ABE+S△ABD- S△ACE，即可求解．
【详解】解：(1)当时，，
解得：．
∴A(-1，0)，B(3，0)，
∵直线：经过点A，
∴，，
∴直线的解析式为 ，
∵直线与抛物线的交点D的横坐标为4，令，
∴，
∴，
∴直线的函数表达式为()；
(2)如图1，过点E作EF∥y轴，交直线于点F，

设E(，)，则F(，)，

S△ACE =S△AFE - S△CFE
= ( )( )- ( )
= ( )
= ( )2，
∴当时，△ACE的面积的最大值为 ，
∵△ACE的面积的最大值为 ，
∴，解得，
∴抛物线的解析式为：；
(3)在(2)的条件下可得：
当时，，
∴点E的坐标为(，)，
解方程，得：
，
∴点D的坐标为(，)，


∴S四边形CDBE=S四边形ADBE- S△ACE=S△ABE+S△ABD- S△ACE
=．
【点评】本题考查了待定系数法求函数解析式，二次函数的图象和性质，二次函数的最值，一次函数的图象和性质，解题的关键是灵活应用待定系数法确定函数解析式．
2．如图1，抛物线y＝ax2﹣2ax﹣3a（a≠0）与x轴交于点A，B．与y轴交于点C．连接AC，BC．已知△ABC的面积为2．
（1）求抛物线的解析式；
（2）平行于x轴的直线与抛物线从左到右依次交于P，Q两点．过P，Q向x轴作垂线，垂足分别为G，H．若四边形PGHQ为正方形，求正方形的边长；
（3）如图2，平行于y轴的直线交抛物线于点M，交x轴于点N （2，0）．点D是抛物线上A，M之间的一动点，且点D不与A，M重合，连接DB交MN于点E．连接AD并延长交MN于点F．在点D运动过程中，3NE+NF是否为定值？若是，求出这个定值；若不是，请说明理由．

【答案】（1）；（2）或；（3）是，3NE+NF为定值4
【分析】（1）先将抛物线解析式变形，可得A和B的坐标，从而得AB=1+3=4，根据三角形ABC的面积为2可得OC的长，确定点C的坐标，根据点C的坐标，利用待定系数法即可求出二次函数的解析式；
（2）设点P的纵坐标为m，当y=m时，﹣x2+x+1=m，解方程可得P和Q两点的坐标，从而得G和H的坐标，再利用正方形的性质可得出关于m的方程，解之即可得出结论；
（3）设点D（n，﹣n2+n+1），利用待定系数法求直线AD和BD的解析式，表示FN和OK的长，直接代入计算可得结论．
【详解】（1）如图1，y=ax2﹣2ax﹣3a=a（x2﹣2x﹣3）=a（x﹣3）（x+1），

∴A（﹣1，0），B（3，0），
∴AB=4，
∵△ABC的面积为2，即，
∴OC=1，
∴C（0，1），
将C（0，1）代入y=ax2﹣2ax﹣3a，得：﹣3a=1，
∴a=﹣，
∴该二次函数的解析式为y=﹣x2+x+1；
（2）如图2，设点P的纵坐标为m，当y=m时，﹣x2+x+1=m，

解得：x1=1+，x2=1﹣，
∴点P的坐标为（1﹣，m），点Q的坐标为（1+，m），
∴点G的坐标为（1﹣，0），点H的坐标为（1+，0），
∵矩形PGHQ为正方形，
∴PQ=PG，　
∴1+﹣（1﹣）=m，
解得：m1=﹣6﹣2，m2=﹣6+2，
∴当四边形PGHQ为正方形时，边长为6+2或2﹣6；
（3）如图3，设点D（n，﹣n2+n+1），延长BD交y轴于K，

∵A（﹣1，0），
设AD的解析式为：y=kx+b，
则，解得：，
∴AD的解析式为：y=（﹣）x﹣，
当x=2时，y=﹣n+2﹣n+1=﹣n+3，
∴F（2，3﹣n），
∴FN=3﹣n，
同理得直线BD的解析式为：y=（﹣）x+n+1，
∴K（0，n+1），
∴OK=n+1，
∵N（2，0），B（3，0），
∴，
∵EN∥OK，
∴，
∴OK=3EN，
∴3EN+FN=OK+FN=n+1+3﹣n=4，
∴在点D运动过程中，3NE+NF为定值4．
【点评】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、正方形的性质、待定系数法求一次函数解析式以及平行线分线段成比例定理等知识，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用正方形的性质，找出关于m的方程；（3）利用AD和BD的解析式确定FN和OK的长，可解决问题．
3．在平面直角坐标系中，已知抛物线经过A（－4，0），B（0，－4），C（2，0）三点．

（1）求抛物线的解析式；
（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．
（3）若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
【答案】（1）；（2），时有最大值；（3）或或或．
【分析】（1）先假设出函数解析式，利用三点法求解函数解析式．
（2）设出M点的坐标，利用S＝S△AOM＋S△OBM−S△AOB即可进行解答；
（3）当OB是平行四边形的边时，表示出PQ的长，再根据平行四边形的对边相等列出方程求解即可；当OB是对角线时，由图可知点A与P应该重合．
【详解】解：（1）设此抛物线的函数解析式为：，
将，，三点代入函数解析式得：
，
解得，
所以此函数解析式为：；
（2）∵点的横坐标为，且点在这条抛物线上，
∴点的坐标为：，
∴




∵，
当时，有最大值为：．
答：时有最大值．
（3）设．
当为边时，根据平行四边形的性质知，且，
∴的横坐标等于的横坐标，
又∵直线的解析式为，则．
由，得，
解得，，．（不合题意，舍去）
如图，当为对角线时，知与应该重合，．


四边形为平行四边形则，横坐标为4，
代入得出为．
由此可得或或或．
【点评】本题考查了三点式求抛物线的方法，以及抛物线的性质和最值的求解方法．
4．如图，直线与轴交于点，与轴交于点，抛物线经过点．

（1）求抛物线的解析式；
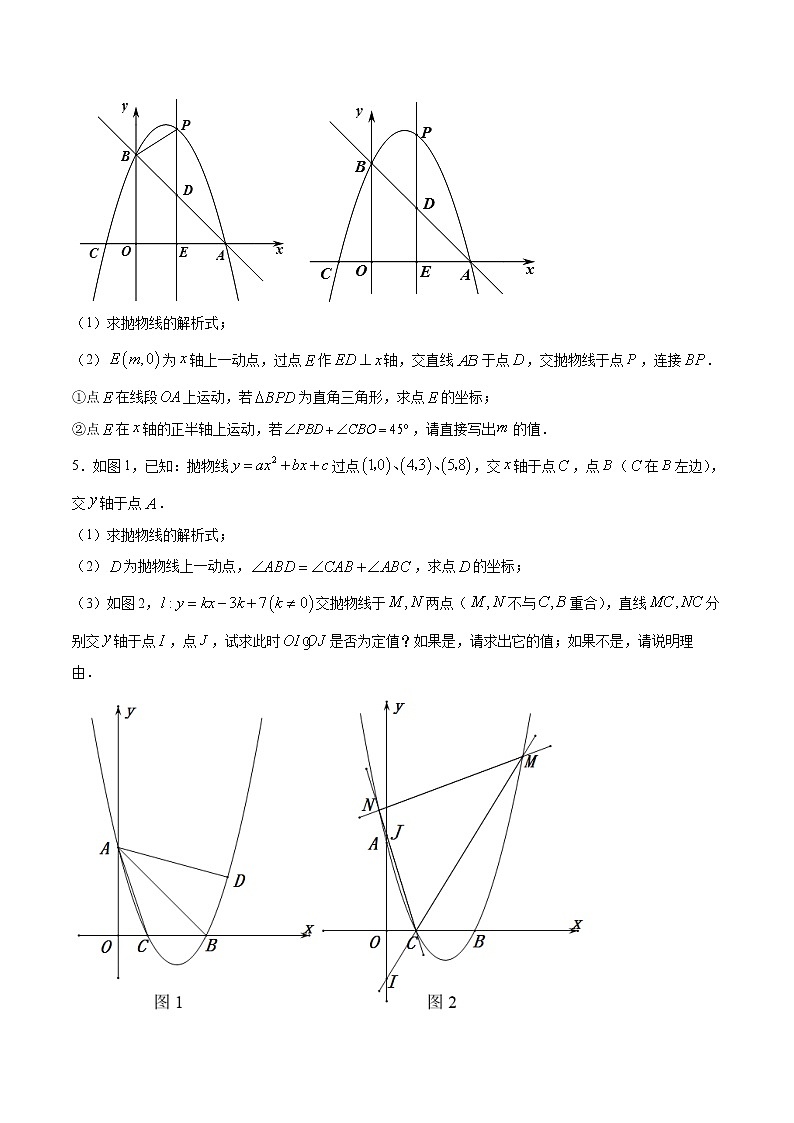
（2）为轴上一动点，过点作轴，交直线于点，交拋物线于点，连接．
①点在线段上运动，若为直角三角形，求点的坐标；
②点在轴的正半轴上运动，若，请直接写出的值．
【答案】（1） ；（2）①点的坐标为或；②的值为5或．
【分析】（1）把点A坐标代入直线解析式可求出n，进而可得点B坐标，再根据待定系数法解答即可；
（2）①由于，故分两种情况考虑，当时，如图1，可得轴，于是可得点的纵坐标为3，代入抛物线的解析式即可求出点P的横坐标，进而可得点E坐标；当时，设直线与轴交于点，如图2，易得△BAH是等腰直角三角形，于是可得点H的坐标，然后利用待定系数法即可求出直线PB的解析式，再联立直线和抛物线的解析式即可求出点P的坐标，进而可得点E坐标；
②若点P在直线BA的上方，如图3，由题意可得PB⊥BC，易求得直线BC的解析式，则直线PB的解析式可得，然后联立直线PB与抛物线的解析式即可求出点P的坐标，进而可得m的值；若点P在直线BA的下方，如图4，由题意易得∠CBO=∠PBO，进而可得直线PB与x轴的交点M的坐标，于是可求出直线PB的解析式，然后联立直线PB与抛物线的解析式即可求出交点P的坐标，从而可得结果．
【详解】解：（1）∵与轴交于点，与轴交于点，
∴，解得，∴．
∵抛物线经过点、，
∴，解得，
∴抛物线的解析式为；
（2）①∵轴，∴．
∴分两种情况考虑，
当时，如图1，则轴，∴点的纵坐标为3．
当时，，解得，．
∴点的坐标为，
∴点的坐标为；

当时，设直线与轴交于点，如图2，

∵OA=OB=3，
∴，
∴．
∴，∴点H的坐标为．
设直线的解析式为，
将，代入，得，解得，
∴直线的解析式为．
解方程组，得，，
∴点的坐标为，
∴点的坐标为．
综上所述：当是直角三角形时，点的坐标为或；
②若点P在直线BA的上方，如图3，
∵，∠ABO=45°，
∴∠CBP=90°，即PB⊥BC，
∵C（﹣1，0），B（0，3），
∴直线BC的解析式是，
∴直线PB的解析式为，
解方程组，得，，
∴点P的坐标为，
∴；

若点P在直线BA的下方，如图4，
∵，∠ABO==45°，
∴∠CBO=∠PBO，
设直线PB交x轴于点M，则OM=OC=1，
∵B（0，3），M（1，0），
∴直线PB的解析式为，
解方程组，得，，
∴点P的坐标为（5，﹣12），
∴m=5；

综上，的值为5或．
【点评】本题是二次函数综合题，主要考查了待定系数法求函数的解析式、函数图象上点的坐标特征、一元二次方程的解法以及直线与抛物线的交点等知识，综合性较强，属于试卷压轴题，熟练掌握二次函数的相关知识、灵活应用数形结合思想是解题的关键．
5．如图1，已知：抛物线过点，交轴于点，点（在左边），交轴于点．
（1）求抛物线的解析式；
（2）为抛物线上一动点，，求点的坐标；
（3）如图2，交抛物线于两点（不与重合），直线分别交轴于点，点，试求此时是否为定值？如果是，请求出它的值；如果不是，请说明理由．

【答案】（1）；（2）不存在点D；（3）是，7
【分析】（1）根据已知条件，将分别代入，解得的值即可；
（2）取作轴于S，构造，计算抛物线与两坐标轴的交点，解得根据题意，证明，从而得到，因为直线，联立直线与抛物线的解析式，求得点D的坐标即可解题；
（3）先联立直线与抛物线的方程组，求得两交点的坐标关系，分别计算直线NC与直线MC的解析式，再代入计算的值即可．
【详解】（1）将代入，
得
（2）取作轴于，

，
在和中

∴

∴，

，

∴，
∴，
而，
∴，∴
∵
∴重合，
∴此时不存在，
∴无解；
（3），设




∴：
同理：：
∴




【点评】本题考查二次函数与一次函数的综合，其中涉及二次函数解析式求法、一次函数解析式求法、全等三角形的判断与性质、等腰直角三角形的性质、平行线判定与性质、一元二次方程的解法、韦达定理等知识，是重要考点，难度较难，作出正确辅助线，掌握相关知识是解题关键．
6．如图，直线y＝﹣x+3与x轴、y轴分别交于点B，点C，经过B，C两点的抛物线y＝x2+bx+c与x轴的另一个交点为A，顶点为P，点M为抛物线的对称轴上的一个动点．
（1）求该抛物线的解析式；
（2）当点M在x轴的上方时，求四边形COAM周长的最小值；
（3）在平面直角坐标系内是否存在点N，使以C，P，M，N为顶点的四边形为菱形？若存在，请写出所有符合条件的点M的坐标；若不存在，请说明理由．

【答案】（1）；见详解；（2）；见详解；（3）存在，点M的坐标为或或或；见详解．
【分析】1）先求出点B，点C坐标，代入解析式可求解；
（2）由抛物线的对称性可得AM＝BM，点A（1，0），由四边形COAM周长＝OC+OA+AM+CM＝4+BM+CM，则点B，点M，点C三点共线时，BM+CM有最小值为BC的长，即四边形COAM周长的最小值＝4+BC，由勾股定理可求解；
（3）由菱形的性质可得△CPM是等腰三角形，分三种情况讨论，由两点距离公式可求解．
【详解】解：（1）∵直线与x轴、y轴分别交于点B，点C，
∴点B，点C，
∵抛物线经过B，C两点，
∴，
解得，
∴抛物线的解析式为：；
（2）如图，连接AM，

∵，
∴抛物线的对称轴为直线x＝2，
∵点A与点B关于对称轴对称，
∴AM＝BM，点A，
∵点C，点A，点B，
∴OA＝1，OC＝3，OB＝3，
∵四边形COAM周长＝OC+OA+AM+CM，
∴四边形COAM周长＝4+BM+CM，
∴当点B，点M，点C三点共线时，BM+CM有最小值为BC的长，
∴四边形COAM周长的最小值＝4+BC，
∵BC＝＝＝，
∴四边形COAM周长的最小值＝；
（3）∵，
∴顶点P，
又∵点C，
∴PC＝＝，
设点M，
∴MC＝＝，
MP＝|t+1|，
∵以C，P，M，N为顶点的四边形为菱形，
∴△CPM是等腰三角形，
若MC＝MP，则＝|t+1|，
∴t＝，
∴点M；
若MP＝PC，则＝|t+1|，
∴， ，
∴点M或；
若MC＝PC，则＝，
解得：（不合题意舍去），，
∴点M；
综上所述：点M的坐标为或或或．
【点评】本题主要考查二次函数与几何的综合运用，熟练掌握二次函数的知识及菱形、等腰三角形的分类讨论是解题的关键．
7．如图1，在平面直角坐标系xOy中，抛物线y＝x2＋k的顶点A在直线：y＝x﹣3上，将抛物线沿直线向右上方平移，使其顶点P始终保持在直线上，设平移后的抛物线与原抛物线交于B点．
（1）请直接写出k的值；
（2）若抛物线y＝x2＋k与直线：y＝x﹣3的另一个交点为C．当点B与点C重合时．求平移后抛物线的解析式；
（3）连接AB，BP，当△ABP为直角三角形时，求出P点的坐标．

【答案】（1）k＝﹣3
（2）y＝x2﹣2x﹣1
（3）（3，0）或（，﹣3）
【分析】（1）先根据直线：y＝x﹣3，可得直线与y轴的交点A的坐标，从而代入抛物线的解析式y＝x2＋k，可得k的值；
（2）将两函数的解析式列方程后可得交点C的坐标，因为点B与点C重合，所以平移后的抛物线的顶点P与C重合，由此可得平移后的抛物线的解析式；
（3）分两种情况：①当∠APB＝90°，如图2，利用勾股定理和两点的距离公式，列方程可得结论；②当∠ABP＝90°，利用勾股定理和两点的距离公式计算量太大，所以作辅助线，构建两个直角三角形，利用等角的正切列比例式可得结论．
【详解】解：（1）直线：y＝x﹣3，
当x＝0时，y＝﹣3，
∴顶点（0，﹣3），
∴抛物线的解析式为：y＝x2﹣3，即k＝﹣3；
（2）由题意得：x2﹣3＝x﹣3，
解得：x1＝0，x2＝1，
∴C（1，﹣2），
当点B与点C重合时，如图1，顶点P（1，﹣2），

∴平移后抛物线的解析式为：y＝（x﹣1）2﹣2＝x2﹣2x﹣1；
（3）∵抛物线顶点P始终保持在直线上，
∴设P（m，m﹣3），则平移后的抛物线的解析式为：y＝（x﹣m）2＋m﹣3，
∴，
解得：，
∴B（，），
∵抛物线x2﹣3沿直线向右上方平移，
∴当△ABP为直角三角形时，∠PAB不可能为直角，
所以分两种情况：
①当∠APB＝90°时，如图2，AP2＋BP2＝AB2，

∴＋＝，
∴m（m﹣1）（m﹣3）＝0，
∴m1＝0（舍），m2＝1（舍），m3＝3，
∴P（3，0）；
②当∠ABP＝90°时，如图3，过B作EF⊥y轴于F，过P作PE⊥EF于E，

∴∠ABF＋∠EBP＝∠EBP＋∠EPB＝90°，
∴∠ABF＝∠EPB，
∴tan∠ABF＝tan∠EPB，即，
∴＝，
解得：m1＝﹣（舍），m2＝，
∴P（，﹣3），
综上，P点的坐标是（3，0）或（，﹣3）．
【点评】本题是二次函数综合题，考查了二次函数的性质，待定系数法求解析式，三角函数，两点距离公式，勾股定理，平移等知识，灵活运用这些性质进行推理是本题的关键．
8．如图1，抛物线与x轴交于A，B两点（点A位于点B的左侧），与y轴负半轴交于点C，若AB＝4．
（1）求抛物线的解析式；
（2）如图2，E是第三象限内抛物线上的动点，过点E作EF∥AC交抛物线于点F，过E作EG⊥x轴交AC于点M，过F作FH⊥x轴交AC于点N，当四边形EMNF的周长最大值时，求点E的横坐标；
（3）在x轴下方的抛物线上是否存在一点Q，使得以Q、C、B、O为顶点的四边形被对角线分成面积相等的两部分？如果存在，求点Q的坐标；如果不存在，请说明理由．

【答案】（1）；见解析；（2）；见解析；（3）存在，点Q的坐标为：（﹣1，﹣4）或（﹣，﹣）或（，）；详解解析．
【分析】（1）＝0，则根据根与系数的关系有AB＝，即可求解；
（2）设点E，点F，四边形EMNF的周长C＝ME+MN+EF+FN，即可求解；
（3）分当点Q在第三象限、点Q在第四象限两种情况，分别求解即可．
【详解】解：（1）依题意得：=0，
则，
则AB＝，
解得：a＝5或﹣3，
抛物线与y轴负半轴交于点C，故a＝5舍去，则a＝﹣3，
则抛物线的表达式为：…①；
（2）由得：点A、B、C的坐标分别为：、，
设点E，OA＝OC，故直线AC的倾斜角为45°，EF∥AC，
直线AC的表达式为：y＝﹣x﹣3，
则设直线EF的表达式为：y＝﹣x+b，将点E的坐标代入上式并解得：
直线EF的表达式为：y＝﹣x+…②，
联立①②并解得：x＝m或﹣3﹣m，
故点F，点M、N的坐标分别为：、，
则EF＝，
四边形EMNF的周长C＝ME+MN+EF+FN＝，
∵﹣2＜0，故S有最大值，此时m＝，
故点E的横坐标为：；
（3）①当点Q在第三象限时，当QC平分四边形面积时，
则，故点Q；
当BQ平分四边形面积时，
则，
则，
解得：，故点Q；
②当点Q在第四象限时，
同理可得：点Q；
综上，点Q的坐标为：或或．
【点评】本题考查的是二次函数的综合运用，涉及到一次函数、图形的面积计算等，其中（1）（3）都要注意分类求解，避免遗漏．
9．如图，在平面直角坐标系xOy中，直线l：y＝x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y＝+bx+c经过点B，且与直线l的另一个交点为C（4，n）．
（1）求n的值和抛物线的解析式；
（2）P是直线AC下方的抛物线上一动点，设其横坐标为a．当a为何值时，△APC的面积最大，并求出其最大值．
（3）M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1，若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．

【答案】（1）2，y＝x2﹣x﹣1；（2）a＝2时，△APC的面积最大，最大值为2；（3）或﹣．
【分析】（1）把点B的坐标代入直线解析式求出m的值，再把点C的坐标代入直线求解即可得到n的值，然后利用待定系数法求二次函数解析式解答；
（2）过点P作PD∥y轴交AC于点D，由题意得P（a，a﹣1），则D（a，a﹣1），得出PD的长，则可求出△APC的面积，由二次函数的性质可得出答案；
（3）根据逆时针旋转角为90°可得A1O1∥y轴时，B1O1∥x轴，然后分①点O1、B1在抛物线上时，表示出两点的横坐标，再根据纵坐标相同列出方程求解即可；②点A1、B1在抛物线上时，表示出点B1的横坐标，再根据两点的纵坐标相差A1O1的长度列出方程求解即可．
【详解】（1）直线l：y=x+m过点B（0，﹣1），
则m=﹣1，
则直线l：y=x﹣1，
将点C（4，n）代入上式并解得：n=2，
故点C（4，2），
将点B、C的坐标代入二次函数表达式得：
，
解得：，
故抛物线的表达式为：y=x2﹣x﹣1；
（2）如图1，过点P作PD∥y轴交AC于点D，
由题意得P（a，a﹣1），则D（a，a﹣1），

∴PD==﹣+2a，
∵A（2，0），C（4，2），
∴△APC的面积为PD×（4﹣2）==﹣+2a=﹣+2，
∴a=2时，△APC的面积最大，最大值为2；
（3）∵△AOB绕点M沿逆时针方向旋转90°，
∴A1O1∥y轴时，B1O1∥x轴，设点A1的横坐标为x，
①如图2，点O1、B1在抛物线上时，点O1的横坐标为x，点B1的横坐标为x+1，

∵点O1和B1的纵坐标相等，
∴x2﹣x﹣1=(x+1)2﹣(x+1)﹣1，
解得x=，
②如图3，点A1、B1在抛物线上时，点B1的横坐标为x+1，点A1的纵坐标比点B1的纵坐标大，
∴x2﹣x﹣1=(x+1)2﹣(x+1)﹣1+，
解得x=﹣，
综上所述，点A1的横坐标为或﹣．
【点评】本题是二次函数综合题型，考查了一次函数图象上点的坐标特征，待定系数法求二次函数解析式，二次函数的性质等知识，熟练掌握方程思想和分类讨论思想是解题的关键．
10．如图，抛物线与轴交于两点，与轴交于点连接．点沿以每秒个单位长度的速度由点向点运动，到达点后再以同样的速度沿轴正半轴运动，同时，点沿以每秒个单位长度的速度由点向点运动，当点停止运动时，点也随之停止运动，连接．过点作轴，与抛物线交于点连接．设点的运动时间为秒，已知点、点的坐标分别为．

（1）求抛物线的解析式．
（2）①直接写出点的坐标（用含的代数式表示，结果需化简）；
②当点在线段上运动，且满足时，求的值．
（3）试探究：在点运动的过程中，是否存在某一时刻，使得的中点落在坐标轴上？若存在，请直接写出此时的值与点的坐标；若不存在，请说明理由．
【答案】（1）；（2）①；②当点在线段上运动，且满足时，的值是；（3）存在．时，；时，
【分析】（1）利用待定系数法代入计算即可；
（2）①过点Q作QH⊥y轴于点H，证得∽利用相似三角形的性质求出HQ及OH，从而表示出点Q的坐标；
②过点Q作QD⊥PM于D，QE⊥x轴于E，得到四边形PDQE是矩形，利用矩形及等腰三角形的性质证得PM=2PE，再根据坐标表示出线段建立方程求解即可；
（3）分“点P在OA上时”和“在y轴正半轴上时”两种情况计算，先根据点P、Q的坐标表示出中点坐标，然后由“中点落在y轴上”或“中点落在x轴上”建立方程求解即可．
【详解】解：（1）将，分别代入，得，
解得，
故抛物线的解析式为；
（2）①过点Q作QH⊥y轴于点H，如图，

则∠CHQ=∠COB=90°，
又∵∠HCQ=∠OCB，
∴∽，
∴，
∵当x=0时，，即C(0，－3)，
∴OC=3，
∵B(4，0)，
∴OB=4，
∴在中，，
又∵，
∴，
∴，,
∴，
∴；
②过点Q作QD⊥PM于D，QE⊥x轴于E，如图，

则四边形是矩形，
∴，
∵，
∴，
∵，
∴，
∴，
解得（舍去），，
∴当点在线段上运动，且满足时，的值是；
（3）存在，时，；时，．
当点P在OA上时，，，中点落在y轴上，
∴中点坐标为，
∴，
∴，，
当点P在y轴正半轴上时，，，中点落在x轴上，
∴中点坐标为，
∴，
∴，，
综上所述，时，；时，．
【点评】本题考查了二次函数与几何动点的综合应用，相似三角形的判定与性质，矩形的判定与性质，等腰三角形的性质，勾股定理，中点公式及坐标轴上点的特征等知识，较为综合，能够熟练应用知识是解题的关键．
11．抛物线y＝ax2－2ax－3a（a＜0）交x轴于点A、B，交y轴于点C，它的对称轴交x轴于点E．
(1) 直接写出点E的坐标为__________
(2) 如图，直线y＝x与抛物线交于点M、N，求OM·ON的值．

(3) 如图2，过点C作CD∥x轴交抛物线于点D，连接DE并延长交y轴于点F，交抛物线于点G．直线AF交CD于点H，交抛物线于点K，连接HE、GK，求证：HE∥GK．

【答案】(1) （1，0）；(2) 6；(3) 见解析.
【分析】（1）利用对称轴公式求解即可．
（2）设M（m,m）、N（n,n）,则OM=，ON=，然后利用一元二次方程根与系数的关系即可求解；
（3）求出直线HF，DF的解析式，利用方程组确定点K，G的坐标，再求出直线EH，GK的解析式即可判断．
【详解】解：（1）对于抛物线y＝ax2－2ax－3a，对称轴x= =1，
∴E（1，0），
故答案为（1，0）．
（2）∵M、N在直线y=x上，
∴设M（m,m）、N（n,n）,
∵M、N是直线y＝x与抛物线y= ax2－2ax－3a的交点，
∴m、n是方程ax2－2ax－3a=x即ax2－（2a+1）x－3a=0的两个根，
∴mn=-3，
∵OM=，ON=，
∴OM·ON====6；
（3）证明：如图，

由题意可得A（-1，0），C（0，-3a），D（2，-3a），E（1，0），
∴直线DE的解析式为y=-3ax+3a，
∴F（0，3a），
∴直线AF的解析式为y=3ax+3a，
∴H（-2，-3a），
∴直线HE的解析式为y=ax-a，
由，
解得或，
∴K（6，21a），
由，
解得或，
∴G（-3，12a），
∴直线GK的解析式为y=ax+15a，
∵直线HE的解析式为y=ax-a，
∴HE∥GK．
【点评】本题属于二次函数综合题，解题的关键是利用方程组确定交点坐标，属于中考压轴题．
12．已知抛物线交x轴于A，B两点（A在B右边），A（3，0），B（1，0）交y轴于C点，C（0，3），连接AC；

（1）求抛物线的解析式；
（2）P为抛物线上的一点，作PE⊥CA于E点，且CE=3PE，求P点坐标；
（3）将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点，过H作直线MH，NH，当MH⊥NH时，求MN恒过的定点坐标．
【答案】（1）y=x2﹣4x+3；（2）（2，﹣1）或（，）；（3）MN恒过的定点（2，1）
【分析】（1）用待定系数解答便可；
（2）分两种情况：P点AC的上方，点P在AC的下方．过点P作PD⊥x轴于点D，过E作EF⊥y轴于F，与PD交于点G，证明EF=3EG，设EG=m，用m的代数式表示P点的横纵坐标，再代入二次函数解析式，便可求得m的值，进而得P点的坐标；
（3）过M作MK⊥x轴于点K，过点N作NL⊥x轴于点L，先求出H点的坐标与新抛物线的解析式，设出M、N的坐标，得出两坐标的联系，表示出MN的解析式，再代入定点（2，1）的坐标进行验证便可得解．
【详解】（1）∵抛物线过A（3，0），B（1，0），
∴可设抛物线的解析式为y=a（x﹣3）（x﹣1）（a≠0），
把c（0，3）代入，得3a=3，
∴a=1，
∴抛物线的解析式是y=（x﹣3）（x﹣1）=x2﹣4x+3，
即y=x2﹣4x+3；
（2）当P点在AC上方时，过点P作PD⊥x轴于点D，过E作EF⊥y轴于F，延长FE与PD交于点G，如图1，

∵A（3，0），C（0，3），
∴OA=OC=3，
∴∠OAC=45°，
∵FG∥OA，
∴∠CEF=45°，
∴CF=EF=CE，
∵PE⊥CA，
∴∠PEG=45°，
∴PG=EG=PE，
∵CE=3PE，
∴EF=3FG，
设EF=3m，则PG=EG=m，FG=4m，
∴DG=OF=OC﹣CF=3﹣3m，
PD=PG+DG=3﹣2m，
∴P（4m，3﹣2m），
把P（4m，3﹣2m）代入y=x2﹣4x+3中得，
3﹣2m=16m2﹣16m+3，
∴m=，或m=0（舍去），
∴P（，）；
当P点AC下方时，如图2，过点P作PD⊥x轴于点D，过E作EF⊥y轴于F，延长FE与PD交于点G，

∵A（3，0），C（0，3），
∴OA=OC=3，
∴∠OAC=45°，
∵FE∥OA，
∴∠CEF=45°，
∴CF=EF=CE，
∵PE⊥CA，
∴∠PEG=45°，
∴PG=EG=PE，
∵CE=3PE，
∴EF=3FG，
设EF=3m，则PG=EG=m，EG=2m，
∴DG=OF=OC﹣CF=3﹣3m，
PD=PG﹣DG=4m﹣3，
∴P（2m，3﹣4m），
把P（2m，3﹣4m）代入y=x2﹣4x+3中得，
3﹣4m=4m2﹣8m+3，
∴m=1，或m=0（舍去），
∴P（2，﹣1）；
综上，P点的坐标为（2，﹣1）或（，）；
（3）∵y=x2﹣4x+3=（x﹣2）2﹣1，
∴抛物线y=x2﹣4x+3的顶点为（2，﹣1），
∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点，
∴H（2，0），
由题意知，点H是新抛物线的顶点，
∴新抛物线的解析式为y=（x﹣2）2，
设M（m，（m﹣2）2），N（n，（n﹣2）2），
过M作MK⊥x轴于点K，过点N作NL⊥x轴于点L，如图3，

则MK=（m﹣2）2，KH=2﹣m，HL=n﹣2，NL=（n﹣2）2，
∵MH⊥NH，
∴∠MHK+∠HMK=∠MHK+∠NHL=90°，
∴∠HMK=∠NHL，
∵∠MKH=∠HLN=90°，
∴△KHM∽△LNH，
∴，
，
∴，
∴，
设直线MN的解析式为：y=kx+b（k≠0），则，
∴，
∴直线MN的解析式为：，
当x=2时，=（m-2）2﹣（m2﹣4m+3）
=m2﹣4m+4﹣m2+4m﹣3=1，
∴MN恒过的定点（2，1）．
【点评】本题是二次函数综合题，考查了待定系数法求二次函数解析式，勾股定理，一次函数图象与性质，相似三角形的性质与判定，平移的性质等相关知识点．第三题难度极大，关键是构造相似三角形，找到M、N两点坐标的联系，运用直线的解析式确定定点坐标．第二题要分两种情况解决，容易漏掉第二种情况的解．
13．如图，抛物线过点A（0，1）和C，顶点为D，直线AC与抛物线的对称轴BD的交点为B（，0），平行于y轴的直线EF与抛物线交于点E，与直线AC交于点F，点F的横坐标为，四边形BDEF为平行四边形．
（1）求点F的坐标及抛物线的解析式；
（2）若点P为抛物线上的动点，且在直线AC上方，当△PAB面积最大时，求点P的坐标及△PAB面积的最大值；
（3）在抛物线的对称轴上取一点Q，同时在抛物线上取一点R，使以AC为一边且以A，C，Q，R为顶点的四边形为平行四边形，求点Q和点R的坐标．

【答案】（1）（，﹣）；y＝﹣x2+2x+1 （2）（，）； （3）Q，R或Q（，﹣10），R（）
【分析】（1）由待定系数法求出直线AB的解析式为y＝﹣x+1，求出F点的坐标，由平行四边形的性质得出﹣3a+1＝a﹣8a+1﹣（﹣），求出a的值，则可得出答案；
（2）设P（n，﹣n2+2n+1），作PP'⊥x轴交AC于点P'，则P'（n，﹣n+1），得出PP'＝﹣n2+n，由二次函数的性质可得出答案；
（3）联立直线AC和抛物线解析式求出C（，﹣），设Q（，m），分两种情况：①当AQ为对角线时，②当AR为对角线时，分别求出点Q和R的坐标即可．
【详解】解：（1）设抛物线的解析式为y＝ax2+bx+c（a≠0），
∵A（0，1），B（，0），
设直线AB的解析式为y＝kx+m，
∴，
解得，
∴直线AB的解析式为y＝﹣x+1，
∵点F的横坐标为，
∴F点纵坐标为﹣+1＝﹣，
∴F点的坐标为（，﹣），
又∵点A在抛物线上，
∴c＝1，
对称轴为：x＝﹣，
∴b＝﹣2a，
∴解析式化为：y＝ax2﹣2ax+1，
∵四边形DBFE为平行四边形．
∴BD＝EF，
∴﹣3a+1＝a﹣8a+1﹣（﹣），
解得a＝﹣1，
∴抛物线的解析式为y＝﹣x2+2x+1；
（2）设P（n，﹣n2+2n+1），作PP'⊥x轴交AC于点P'，

则P'（n，﹣n+1），
∴PP'＝﹣n2+n，
S△ABP＝OB•PP'＝﹣n＝﹣，
∴当n＝时，△ABP的面积最大为，此时P（，）．
（3）∵，
∴x＝0或x＝，
∴C（，﹣），
设Q（，m），
①当AQ为对角线时，
∴R（﹣），
∵R在抛物线y＝+4上，
∴m+＝﹣+4，
解得m＝﹣，
∴Q，R；
②当AR为对角线时，
∴R（），
∵R在抛物线y＝+4上，
∴m﹣+4，
解得m＝﹣10，
∴Q（，﹣10），R（）．
综上所述，Q，R；或Q（，﹣10），R（）．
【点评】本题是二次函数综合题，考查了待定系数法，二次函数的性质，二次函数图象上点的坐标特征，平行四边形的性质等知识，熟练掌握二次函数的性质及方程思想，分类讨论思想是解题的关键．
14．如图，已知抛物线y＝ax2+bx+5经过A（﹣5，0），B（﹣4，﹣3）两点，与x轴的另一个交点为C，顶点为D，连接BD，CD．

（1）求该抛物线的表达式；
（2）判断△BCD的形状，并说明理由；
（3）点为该抛物线上一动点P （与点B、C不重合），该抛物线上是否存在点P，使得∠PBC＝∠BCD？若存在，请直接写出满足条件的所有点P的坐标；若不存在，请说明理由．
【答案】（1）y＝x2+6x+5；（2）直角三角形，理由见解析；（3）存在，点P的坐标为（﹣，﹣）或（0，5）
【分析】（1）由题意利用待定系数法将点A、B坐标代入二次函数表达式，即可求解；
（2）根据题意令y＝0，则x2+6x+5＝0，解得x得出点C，进而利用勾股定理逆定理进行判断即可；
（3）根据题意分点P在直线BC下方、上方两种情况，分别进行分析求解即可．
【详解】解：（1）将点A、B坐标代入二次函数表达式得：
，解得：，
故抛物线的表达式为：y＝x2+6x+5①．
（2）令y＝0，则x2+6x+5＝0，解得x＝﹣1或﹣5，
即点C（﹣1，0），
∵y＝（x+3）2﹣4，
∴D（﹣3，﹣4），
∵B（﹣4，﹣3），
∴BD＝＝，BC＝＝3，CD＝＝2，
∴CD2＝BD2+BC2，
∴∠CBD＝90°，
∴△CBD是直角三角形．
（3）设直线BP与CD交于点H，

当点P在直线BC下方时，
∵∠PBC＝∠BCD，
∴点H在BC的中垂线上，
线段BC的中点坐标为（﹣，﹣），
过该点与BC垂直的直线的k值为﹣1，
设BC中垂线的表达式为：y＝﹣x+m，将点（﹣，﹣）代入上式并解得：
直线BC中垂线的表达式为：y＝﹣x﹣4③，
同理直线CD的表达式为：y＝2x+2④，
联立③④并解得：x＝﹣2，即点H（﹣2，﹣2），
同理可得直线BH的表达式为：y＝x﹣1⑤，
联立①⑤并解得：x＝﹣或﹣4（舍去﹣4），
故点P（﹣，﹣）；
当点P（P′）在直线BC上方时，
∵∠PBC＝∠BCD，
∴BP′//CD，
则直线BP′的表达式为：y＝2x+s，将点B坐标代入上式并解得：s＝5，
即直线BP′的表达式为：y＝2x+5⑥，
联立①⑥并解得：x＝0或﹣4（舍去﹣4），
故点P（0，5）；
故点P的坐标为（﹣，﹣）或（0，5）．
【点评】本题属于二次函数综合题，考查二次函数的性质，涉及到一次函数、等腰三角形性质、图形的面积计算等，同时解题时要注意分类讨论求解，避免遗漏．
15．如图，在平面直角坐标系中，直线交x轴，y轴于A，C两点，二次函数的图象经过A，C两点，与x轴另一个交点是B．动点P从A点出发，沿以每秒2个单位长度的速度，向终点B运动，过点P作于点D．（点P不与点A，B重合）作，边交射线于点Q．设P点运动时间为t．

（1）求二次函数关系式；
（2）设与重叠面积为S，求S与t之间函数关系；
（3）拋物线上是否存在点M，使，若存在，直接写出点M坐标；若不存在，说明理由．
【答案】（1）；（2）；（3）存在，，
【分析】（1）确定点A、C坐标，再把抛物线经过两点，坐标代入求解即可；
（2）分情况讨论，当时，在中，利用三角函数值求出PD、AD的值，再利用面积公式解答即可；当时，计算CQ的值，在中，三角形PDQ面积减三角形ECQ的面积即可；
（3）根据分两种情况设出直线解析式并求出解析式，联立抛物线即可求出点M的坐标．
【详解】解：（1）∵直线与x轴，y轴交于点A，C
∴，
∵二次函数经过A，C两点
∴解得
∴二次函数关系式为：；
（2）在中，
∴
∵
∴
∴
当点Q和点C重合时，，
当时
在中，，
∴，

当时，
在中，，
∴CE=CQ tan∠CQE，
∴2（t-1）
∴
∴

（3），
∵∠OAC=30°，即∠BAC=30°,
若M在第二象限，设M ，作MN⊥x轴于点N，如图，
∴MN=- ，ON=-x，
∴BN=ON+OB=1-x，
在Rt△MNB中，tan∠ABM=，
即：
解得：x=-2或x=1（舍去）
当x=-2时，-=- ，
∴M点的坐标为（-2， ）；

若M在第三象限，设M，作M’N’⊥x轴于点N’，
此时，M´N´=-（-）=，
ON´=-x，BN´=1-x，
∴tan∠ABM´= ，即 ，
解得：（舍去），
当x=-4时，
-=-=-；
此时，M´（-4，）
故M（-2， ）或（-4，）．
【点评】此题主要考查二次函数的综合问题，会根据点求抛物线和直线的解析式，会运用变量表示三角形面积并解决最值问题，会根据角相等分析点的坐标的存在性是解题的关键．