广东省佛山市顺德区2021-2022学年九年级下学期第一次教学质量数学试题(word版含答案)

这是一份广东省佛山市顺德区2021-2022学年九年级下学期第一次教学质量数学试题(word版含答案)，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年广东省佛山市顺德区中考数学一模试卷
一、选择题（12个题，每题3分，共36分）
1．（3分）如果a与﹣2互为相反数，那么a等于（　　）
A．﹣2 B．2 C．−12 D．12
2．（3分）(−3)2的结果是（　　）
A．﹣3 B．9 C．3 D．﹣9
3．（3分）下面几何体的俯视图是圆的是（　　）
A． B．
C． D．
4．（3分）抛物线y＝3（x﹣1）2+1的顶点坐标是（　　）
A．（1，1） B．（﹣1，1） C．（﹣1，﹣1） D．（1，﹣1）
5．（3分）如图，直线AB∥CD，AB平分∠EAD．若∠1＝100°，则∠2的度数是（　　）

A．30° B．40° C．50° D．60°
6．（3分）已知扇形的圆心角为100°，半径为9，则弧长为（　　）
A．452π B．5π C．8π D．10π
7．（3分）2022年北京冬奥会激起我校学生学习冬奥知识的热情．为了引领学生更深入地学习，组织了一次知识竞赛，随机抽取6名同学的分数（单位：分）如下：80，90，85，92，86，88，则这6个数据的中位数是（　　）
A．85 B．86 C．87 D．88.5
8．（3分）如图，将正方形ABCD剪去4个全等的直角三角形（图中阴影部分），得到边长为c的四边形EFGH．下列等式成立的是（　　）

A．a+b＝c B．c2＝（a+b）2﹣4ab
C．c2＝（a+b）（a﹣b） D．a2+b2＝c2
9．（3分）化简x2+4x+4x+2÷x2+2xx−2−1的结果是（　　）
A．x−2x B．−2x C．﹣3 D．x﹣3
10．（3分）如图，AB⊥CD，且AB＝CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE＝a，BF＝b，EF＝c，则AD的长为（　　）

A．a+c B．b+c C．a﹣b+c D．a+b﹣c
11．（3分）如图，数轴上的点A、B分别表示数1、﹣2x+3．则表示数﹣x+2的点P与线段AB的位置关系是（　　）

A．P在线段AB上
B．P在线段AB的延长线上
C．P在线段AB的反向延长线上
D．不能确定
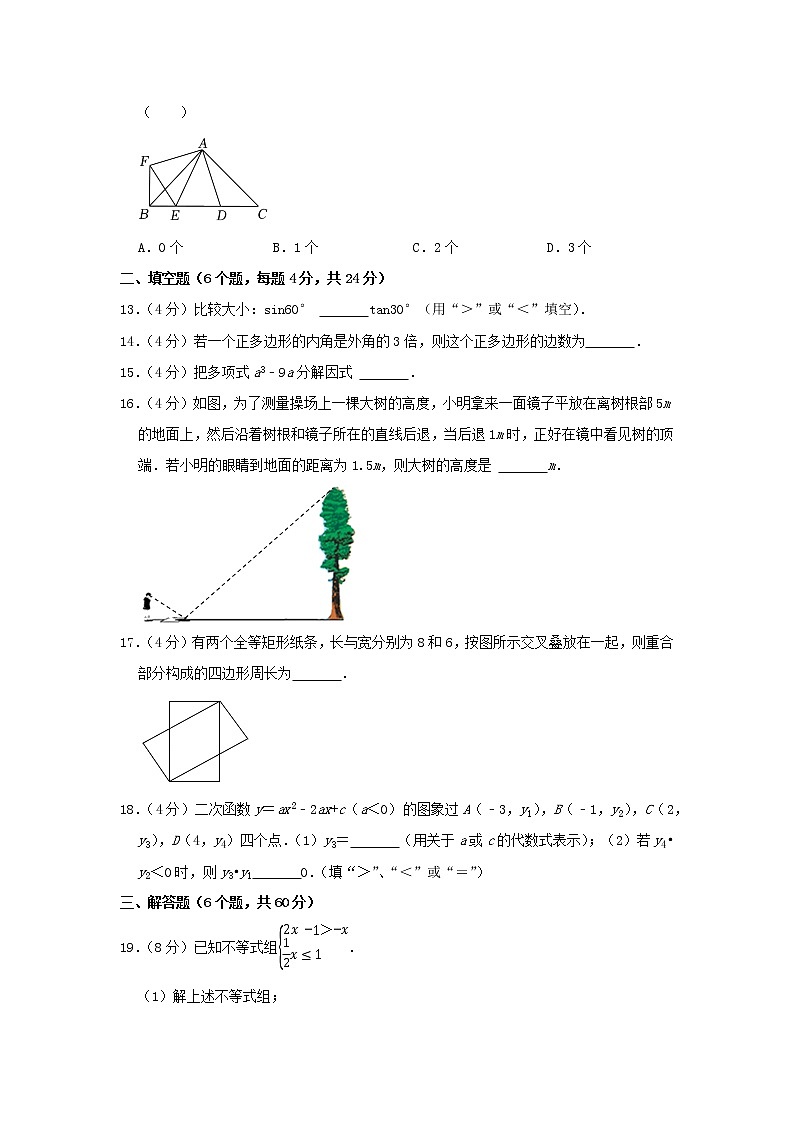
12．（3分）在△ABC中，∠BAC＝90°，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°得到△AFB，连接EF．下列结论：①BE⊥BF；②△ABC的面积等于四边形AFBD的面积；③当BE＝CD时，线段DE的长度最短．其中正确的个数是（　　）

A．0个 B．1个 C．2个 D．3个
二、填空题（6个题，每题4分，共24分）
13．（4分）比较大小：sin60° 　 　tan30°（用“＞”或“＜”填空）．
14．（4分）若一个正多边形的内角是外角的3倍，则这个正多边形的边数为　 　．
15．（4分）把多项式a3﹣9a分解因式 　 　．
16．（4分）如图，为了测量操场上一棵大树的高度，小明拿来一面镜子平放在离树根部5m的地面上，然后沿着树根和镜子所在的直线后退，当后退1m时，正好在镜中看见树的顶端．若小明的眼睛到地面的距离为1.5m，则大树的高度是 　 　m．

17．（4分）有两个全等矩形纸条，长与宽分别为8和6，按图所示交叉叠放在一起，则重合部分构成的四边形周长为　 　．

18．（4分）二次函数y＝ax2﹣2ax+c（a＜0）的图象过A（﹣3，y1），B（﹣1，y2），C（2，y3），D（4，y4）四个点．（1）y3＝　 　（用关于a或c的代数式表示）；（2）若y4•y2＜0时，则y3•y1　 　0．（填“＞”、“＜”或“＝”）
三、解答题（6个题，共60分）
19．（8分）已知不等式组2x−1＞−x12x≤1．
（1）解上述不等式组；
（2）从（1）的结果中选择一个整数是方程1−xx−2=m2−x−2的解，求m的值．
20．（8分）如图，A，B，C，D是⊙O上的四个点，∠ADB＝∠BDC＝60°，过点A作AE∥BC交CD延长线于点E．
（1）求∠ABC的大小；
（2）证明：AE是⊙O的切线．

21．（10分）为落实“垃圾分类回收，科学处理”的政策，某花园小区购买A、B两种型号的垃圾分类回收箱20只进行垃圾分类投放，共支付费用4320元．A、B型号价格信息如表：
型号
价格
A型
200元/只
B型
240元/只
（1）请问小区购买A型和B型垃圾回收箱各多少只？
（2）因受到居民欢迎，准备再次购进A、B两种型号的垃圾分类回收箱共40只，其中A类的数量不大于B类的数量的2倍．求购买多少只A类回收箱支出的费用最少，最少费用是多少元？
22．（10分）抛物线C1：y＝﹣ax2﹣4（a﹣1）x﹣a+5（a≠0）．
（1）将C1先向右平移m个单位．再向下平移n个单位得到C2，点A（3，4﹣n）和点B（4，6﹣2n）在C2上．当C1的对称轴为y轴时，求C2的表达式；
（2）求证：不论a为何值，抛物线C1与x轴总有公共点．
23．（12分）已知∠MON＝90°，点A，B分别在射线OM，ON上（不与点O重合），且OA＞OB，OP平分∠MON，线段AB的垂直平分线分别与OP，AB，OM交于点C，D，E，连接CB，在射线ON上取点F，使得OF＝OA，连接CF．
（1）依题意补全图形；
（2）求证：CB＝CF；
（3）用等式表示线段CF与AB之间的数量关系，并证明．

24．（12分）如图，点O是平面直角坐标系的原点，P是反比例函数y=kx（k＞0，x＞0）图象上的动点，以P为圆心，PO为半径的圆与x、y轴分别交于点A，B，连接AB．
（1）求△OAB的面积；
（2）当k＝4时，求线段AB的最小值；
（3）在（2）的条件下，点C是反比例函数图象上的一点（不与点P重合），连接PC，AC．当∠ACP是直角时，求点C横坐标的近似值（结果保留一位小数）．



2022年广东省佛山市顺德区中考数学一模试卷
答案与详解
一、选择题（12个题，每题3分，共36分）
1．（3分）如果a与﹣2互为相反数，那么a等于（　　）
A．﹣2 B．2 C．−12 D．12
【分析】一个数的相反数就是在这个数前面添上“﹣”号．
【解答】解：﹣2的相反数是2，那么a等于2．
故选：B．
2．（3分）(−3)2的结果是（　　）
A．﹣3 B．9 C．3 D．﹣9
【分析】根据a2=|a|计算即可．
【解答】解：(−3)2=|﹣3|＝3．
故选：C．
3．（3分）下面几何体的俯视图是圆的是（　　）
A． B．
C． D．
【分析】直接利用俯视图即从物体的上面观察得到视图判断即可．
【解答】解：A．俯视图是圆，故本选项符合题意；
B．俯视图是带圆心的圆，故本选项不符合题意；
C．俯视图是三角形，故本选项不符合题意；
D．俯视图是矩形，故本选项不符合题意；
故选：A．
4．（3分）抛物线y＝3（x﹣1）2+1的顶点坐标是（　　）
A．（1，1） B．（﹣1，1） C．（﹣1，﹣1） D．（1，﹣1）
【分析】已知抛物线顶点式y＝a（x﹣h）2+k，顶点坐标是（h，k）．
【解答】解：∵抛物线y＝3（x﹣1）2+1是顶点式，
∴顶点坐标是（1，1）．故选：A．
5．（3分）如图，直线AB∥CD，AB平分∠EAD．若∠1＝100°，则∠2的度数是（　　）

A．30° B．40° C．50° D．60°
【分析】根据邻补角的定义、角平分线的定义及平行线的性质求解即可．
【解答】解：∵∠1＝100°，
∴∠EAD＝180°﹣∠1＝80°，
∵AB平分∠EAD，
∴∠EAB＝∠BAD=12∠EAD＝40°，
∵AB∥CD，
∴∠2＝∠EAB＝40°，
故选：B．
6．（3分）已知扇形的圆心角为100°，半径为9，则弧长为（　　）
A．452π B．5π C．8π D．10π
【分析】根据扇形的弧长公式l=nπr180，直接代入求出即可．
【解答】解：根据扇形的弧长公式可得：l=nπr180=100π×9180=5π，
故选：B．
7．（3分）2022年北京冬奥会激起我校学生学习冬奥知识的热情．为了引领学生更深入地学习，组织了一次知识竞赛，随机抽取6名同学的分数（单位：分）如下：80，90，85，92，86，88，则这6个数据的中位数是（　　）
A．85 B．86 C．87 D．88.5
【分析】根据中位数的定义先把这组数据从小到大排列，再求出最中间两个数的平均数即可．
【解答】解：将这组数据从小到大排列为：80，85，86，88，90，92，
最中间两个数的平均数是：（86+88）÷2＝87，
则中位数是87；
故选：C．
8．（3分）如图，将正方形ABCD剪去4个全等的直角三角形（图中阴影部分），得到边长为c的四边形EFGH．下列等式成立的是（　　）

A．a+b＝c B．c2＝（a+b）2﹣4ab
C．c2＝（a+b）（a﹣b） D．a2+b2＝c2
【分析】用两种方法表示剩下正方形的面积，列出等式，化简即可得到答案．
【解答】解：由图可得剩下正方形面积为：（a+b）2﹣4×12ab，
根据正方形面积公式，剩下正方形面积也可以表示为：c2，
∴（a+b）2﹣4×12ab＝c2，化简得a2+b2＝c2，
故选：D．
9．（3分）化简x2+4x+4x+2÷x2+2xx−2−1的结果是（　　）
A．x−2x B．−2x C．﹣3 D．x﹣3
【分析】把能分解的进行分解，除法转为乘法，再约分即可．
【解答】解：x2+4x+4x+2÷x2+2xx−2−1
=(x+2)2x+2⋅x−2x(x+2)−1
=x−2x−1
=x−2−xx
=−2x，
故选：B．
10．（3分）如图，AB⊥CD，且AB＝CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE＝a，BF＝b，EF＝c，则AD的长为（　　）

A．a+c B．b+c C．a﹣b+c D．a+b﹣c
【分析】只要证明△ABF≌△CDE，可得AF＝CE＝a，BF＝DE＝b，推出AD＝AF+DF＝a+（b﹣c）＝a+b﹣c；
【解答】解：∵AB⊥CD，CE⊥AD，BF⊥AD，
∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，
∴∠A＝∠C，∵AB＝CD，
∴△ABF≌△CDE，
∴AF＝CE＝a，BF＝DE＝b，
∵EF＝c，
∴AD＝AF+DF＝a+（b﹣c）＝a+b﹣c，
故选：D．
11．（3分）如图，数轴上的点A、B分别表示数1、﹣2x+3．则表示数﹣x+2的点P与线段AB的位置关系是（　　）

A．P在线段AB上
B．P在线段AB的延长线上
C．P在线段AB的反向延长线上
D．不能确定
【分析】根据绝对值的几何意义得出：PA＝|﹣x+1|，PB＝|﹣x+1|，AB＝2|﹣x+1|，推出PA+PB＝AB，即点P在线段AB上．
【解答】解：∵PA＝|﹣x+2﹣1|＝|﹣x+1|，PB＝|（﹣x+2）﹣（﹣2x+3）|＝|x﹣1|＝|﹣x+1|，AB＝|﹣2x+3﹣1＝2|﹣x+1|，
∴PA+PB＝AB，
∴点P在线段AB上．
故选：A．
12．（3分）在△ABC中，∠BAC＝90°，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°得到△AFB，连接EF．下列结论：①BE⊥BF；②△ABC的面积等于四边形AFBD的面积；③当BE＝CD时，线段DE的长度最短．其中正确的个数是（　　）

A．0个 B．1个 C．2个 D．3个
【分析】由旋转的性质可得∠ABF＝∠ACB＝45°，可求∠FBE＝90°，可得BE⊥BF，故①正确；由旋转的性质可得△ADC≌△ABF，由面积的和差关系可得△ABC的面积等于四边形AFBD的面积，故②正确；由“SAS”可证△FAE≌△DAE，可得DE＝EF，由勾股定理可得BE2+DC2＝DE2，即可求解．
【解答】解：∵∠BAC＝90°，AB＝AC，
∴∠ABC＝∠ACB＝45°，
∵将△ADC绕点A顺时针旋转90°得到△AFB，
∴∠ABF＝∠ACB＝45°，
∴∠FBE＝∠ABF+∠ABC＝90°，
∴BE⊥BF，故①正确；
∵将△ADC绕点A顺时针旋转90°得到△AFB，
∴△ADC≌△ABF，
∴S△ADC＝S△AFB，
∴S△ADB+S△ADC＝S△ADB+S△ABF，
∴△ABC的面积等于四边形AFBD的面积，故②正确；
∵△AFB≌△ADC，
∴BF＝DC，∠CAD＝∠BAF，∠DAF＝90°，
∵∠BAC＝90°，∠DAE＝45°，
∴∠BAE+∠DAC＝45°，
∴∠EAF＝∠BAF+∠BAE＝∠DAC+∠BAE＝45°，
即∠FAE＝∠DAE＝45°，
在△FAE和△DAE中
AE=AE∠FAE=∠DAEAF=AD，
∴△FAE≌△DAE（SAS），
∴DE＝EF，
在Rt△FBE中，由勾股定理得：BE2+BF2＝EF2，
∵BF＝DC，EF＝DE，
∴BE2+DC2＝DE2，
∵（BE﹣DC）2≥0，
∴BE2+DC2≥2BE•DC，
∴BE＝DC时，BE2+DC2有最小值，
∴当BE＝CD时，线段DE的长度最短，故③正确，
故选：D．
二、填空题（6个题，每题4分，共24分）
13．（4分）比较大小：sin60° 　＞　tan30°（用“＞”或“＜”填空）．
【分析】根据60°的正弦值和30°的正切值进行大小比较．
【解答】解：∵sin60°=32，tan30°=33，
而32＞33，
∴sin60°＞tan30°．
故答案为：＞．
14．（4分）若一个正多边形的内角是外角的3倍，则这个正多边形的边数为　8　．
【分析】设正多边形的边数为n，利用多边形的内角和公式和外角和定理即可解答．
【解答】解：设正多边形的边数为n，由题意得：
（n﹣2）•180°＝3×360°，
解得：n＝8，
故答案为：8．
15．（4分）把多项式a3﹣9a分解因式 　a（a+3）（a﹣3）　．
【分析】原式提取a，再利用平方差公式分解即可．
【解答】解：原式＝a（a2﹣9）
＝a（a+3）（a﹣3）．
故答案为：a（a+3）（a﹣3）．
16．（4分）如图，为了测量操场上一棵大树的高度，小明拿来一面镜子平放在离树根部5m的地面上，然后沿着树根和镜子所在的直线后退，当后退1m时，正好在镜中看见树的顶端．若小明的眼睛到地面的距离为1.5m，则大树的高度是 　7.5　m．

【分析】入射角等于反射角，两个直角相等，那么图中的两个三角形相似，利用对应边成比例可求得树高．
【解答】解：∵∠ABC＝∠DBE，∠ACB＝∠DEB＝90°，
∴△ABC∽△DBE，
∴BC：BE＝AC：DE，
即1：5＝1.5：DE，
∴DE＝7.5（m），
故答案为：7.5．

17．（4分）有两个全等矩形纸条，长与宽分别为8和6，按图所示交叉叠放在一起，则重合部分构成的四边形周长为　25　．

【分析】由题意得出∠A＝90°，AB＝BE＝6，AD∥BC，BF∥DE，AD＝8，证四边形BGDH是菱形，得出BH＝DH＝DG＝BG，设BH＝DH＝x，则AH＝8﹣x，在Rt△ABH中，由勾股定理得出方程，解方程求出BG，即可得出答案．
【解答】解：如图所示：
由题意得：矩形ABCD≌矩形BEDF，
∴∠A＝90°，AB＝BE＝6，AD∥BC，BF∥DE，AD＝8，
∴四边形BGDH是平行四边形，
∴平行四边形BGDH的面积＝BG×AB＝BH×BE，
∴BG＝BH，
∴四边形BGDH是菱形，
∴BH＝DH＝DG＝BG，
设BH＝DH＝x，则AH＝8﹣x，
在Rt△ABH中，由勾股定理得：62+（8﹣x）2＝x2，
解得：x=254，
∴BG=254，
∴四边形BGDH的周长＝4BG＝25；
故答案为：25．

18．（4分）二次函数y＝ax2﹣2ax+c（a＜0）的图象过A（﹣3，y1），B（﹣1，y2），C（2，y3），D（4，y4）四个点．（1）y3＝　c　（用关于a或c的代数式表示）；（2）若y4•y2＜0时，则y3•y1　＜　0．（填“＞”、“＜”或“＝”）
【分析】将x＝2代入抛物线解析式可得y3＝c，根据抛物线解析式可得抛物线开口方向及对称轴，根据各点到对称轴的距离可判断y1＞y4＞y2＞y3，进而求解．
【解答】解：将x＝2代入y＝ax2﹣2ax+c得y＝c，
∴y3＝c，
∵y＝ax2﹣2ax+c（a＜0），
∴抛物线开口向下，对称轴为直线x=−2a−2a=1，
∴与抛物线对称轴距离越近的点的纵坐标越大，
∵1﹣（﹣3）＞4﹣1＞1﹣（﹣1）＞2﹣1，
∴y1＞y4＞y2＞y3，
若y4•y2＜0，则y1＞y4＞0＞y2＞y3，
∴y3•y1＜0，
故答案为：c，＜．
三、解答题（6个题，共60分）
19．（8分）已知不等式组2x−1＞−x12x≤1．
（1）解上述不等式组；
（2）从（1）的结果中选择一个整数是方程1−xx−2=m2−x−2的解，求m的值．
【分析】（1）根据解一元一次不等式组的一般步骤进行解答即可；
（2）先求出（1）中不等式组的整数解，再考虑分母x﹣2≠0，然后把整数代入分式方程得出关于m的方程，解方程即可求出m的值．
【解答】解：（1）2x−1＞−x①12x≤1②，
解不等式①得：x＞13，
解不等式②得：x≤2，
∴不等式组的解集为13＜x≤2；
（2）∵13＜x≤2；
∴x的整数值为1和2，
∵x﹣2≠0，即x≠2，
∴把x＝1代入方程1−xx−2=m2−x−2得：m﹣2＝0，
解得：m＝2．
20．（8分）如图，A，B，C，D是⊙O上的四个点，∠ADB＝∠BDC＝60°，过点A作AE∥BC交CD延长线于点E．
（1）求∠ABC的大小；
（2）证明：AE是⊙O的切线．

【分析】（1）根据圆周角定理得到∠CAB＝∠BDC＝60°，∠ACB＝∠ADB＝60°，根据等边三角形的性质解答即可；
（2）连接AO并延长交BC于F，根据垂径定理的推论得到AF⊥BC，根据平行线的性质得到AF⊥AE，根据切线的判定定理证明结论．
【解答】（1）解：由圆周角定理得：∠CAB＝∠BDC＝60°，∠ACB＝∠ADB＝60°，
∴△ABC为等边三角形，
∴∠ABC＝60°；
（2）证明：连接AO并延长交BC于F，
∵AB＝AC，
∴AB=AC，
∴AF⊥BC，
∵AE∥BC，
∴AF⊥AE，
∵OA是⊙O的半径，
∴AE是⊙O的切线．

21．（10分）为落实“垃圾分类回收，科学处理”的政策，某花园小区购买A、B两种型号的垃圾分类回收箱20只进行垃圾分类投放，共支付费用4320元．A、B型号价格信息如表：
型号
价格
A型
200元/只
B型
240元/只
（1）请问小区购买A型和B型垃圾回收箱各多少只？
（2）因受到居民欢迎，准备再次购进A、B两种型号的垃圾分类回收箱共40只，其中A类的数量不大于B类的数量的2倍．求购买多少只A类回收箱支出的费用最少，最少费用是多少元？
【分析】（1）根据题意列方程组x+y=20200x+240y=4320，解方程组即可；
（2）设购买m只A型回收箱，则购买了（40﹣m）只B型回收箱，根据题意，得m≤2（40﹣m），求出m的取值范围，再表示总费用w＝﹣40m+9600，根据一次函数的增减性即可求解．
【解答】解：设小区购买A型垃圾回收箱x只，B型垃圾回收箱y只，
根据题意，得x+y=20200x+240y=4320，
解得x=12y=8，
∴小区购买A型垃圾回收箱12只，B型垃圾回收箱8只．
（2）设购买m只A型回收箱，则购买了（40﹣m）只B型回收箱，
则有m≤2（40﹣m），
解不等式得m≤803，
设总费用w＝200m+240（40﹣m）＝﹣40m+9600，
∵﹣40＜0，
∴w随着m的增大而减小，
∴当m＝26时，w最小，
此时w最小值＝﹣40×26+9600＝8560．
∴购买A型回收箱26只时，总费用最小为8560元．
22．（10分）抛物线C1：y＝﹣ax2﹣4（a﹣1）x﹣a+5（a≠0）．
（1）将C1先向右平移m个单位．再向下平移n个单位得到C2，点A（3，4﹣n）和点B（4，6﹣2n）在C2上．当C1的对称轴为y轴时，求C2的表达式；
（2）求证：不论a为何值，抛物线C1与x轴总有公共点．
【分析】（1）由C1的对称轴为y轴可得a的值，从而且求出C1解析式，根据抛物线的平移可得C2的解析式，将点A（3，4﹣n）和点B（4，6﹣2n）代入解析式求解．
（2）令y＝0，通过抛物线与x轴交点个数与Δ的关系求解．
【解答】解：（1）∵y＝﹣ax2﹣4（a﹣1）x﹣a+5，
∴C1的对称轴为直线x=−−4(a−1)−2a，
∵C1的对称轴为y轴，
∴a﹣1＝0，
解得a＝1，
∴C1解析式为y＝﹣x2+4，
∵C2的图象是由C1先向右平移m个单位．再向下平移n个单位得到，
∴C2的表达式为y＝﹣（x﹣m）2+4﹣n，
∵点A（3，4﹣n）和点B（4，6﹣2n）在C2上，
∴−(3−m)2+4−n=4−n−(4−m)2+4−n=6−2n，
解得m=3n=3，
∴C2的表达式为y＝﹣（x﹣3）2+1．
（2）证明：将y＝0代入y＝﹣ax2﹣4（a﹣1）x﹣a+5得﹣ax2﹣4（a﹣1）x﹣a+5＝0，
∴Δ＝[﹣4（a﹣1）]2﹣4（﹣a）（﹣a+5）
＝16（a﹣1）2+4a（﹣a+5）
＝12a2﹣12a+16
＝12（a−12）2+13，
∵12（a−12）2+13＞0，
∴抛物线C1与x轴总有2个交点．
23．（12分）已知∠MON＝90°，点A，B分别在射线OM，ON上（不与点O重合），且OA＞OB，OP平分∠MON，线段AB的垂直平分线分别与OP，AB，OM交于点C，D，E，连接CB，在射线ON上取点F，使得OF＝OA，连接CF．
（1）依题意补全图形；
（2）求证：CB＝CF；
（3）用等式表示线段CF与AB之间的数量关系，并证明．

【分析】（1）根据几何语言画出对应的几何图形；
（2）过点C作CE垂直平分AB，CF⊥OP，垂足分别为D，C，根据线段的垂直平分线的性质得到CA＝CB，根据角平分线的定义得到∠AOC＝∠FOC，则可判断△AOC≌△FOC，从而得到CB＝CF；
（3）证明∠ACB＝90°，结合（2）证明三角形ABC是等腰直角三角形，进而可得线段CF与AB之间的数量关系．
【解答】（1）解：如图即为补全的图形；

（2）证明：连接CA，
∵OP是∠MON的平分线，
∴∠AOC＝∠FOC，
在△AOC和△FOC中，
OA=OF∠AOC=∠FOCOC=OC，
∴△AOC≌△FOC（SAS），
∴CA＝CF，
∵CD是线段AB的垂直平分线，
∴CA＝CB，
∴CB＝CF；
（3）AB=2CF，
证明：∵△AOC≌△FOC，
∴∠CAO＝∠CFB，
∵CF＝CB，
∴∠CBF＝∠CFB，
∴∠CAO＝∠CBF，
∵∠CBF+∠CBO＝180°，
∴∠CAO+∠CBO＝180°，
∴∠AOB+∠ACB＝180°，
∵∠AOB＝90°，
∴∠ACB＝90°，
∵CA＝CB，
∴△ABC是等腰直角三角形，
∴AB=2CB，
∴AB=2CF．
24．（12分）如图，点O是平面直角坐标系的原点，P是反比例函数y=kx（k＞0，x＞0）图象上的动点，以P为圆心，PO为半径的圆与x、y轴分别交于点A，B，连接AB．
（1）求△OAB的面积；
（2）当k＝4时，求线段AB的最小值；
（3）在（2）的条件下，点C是反比例函数图象上的一点（不与点P重合），连接PC，AC．当∠ACP是直角时，求点C横坐标的近似值（结果保留一位小数）．


【分析】（1）作PD⊥OA于D，可知AB是直径，得PO＝PA，则S△POA＝k，可得答案；
（2）由OP=12AB，当OP最小时，AB的值最小，求出点P的坐标，从而得出OP的最小值；
（3）过点C作CH⊥x轴于H，过点P作PG∥x轴，交CH于G，则△PCG∽△CAH，设C（m，4m），得出m的方程并化简得，m2﹣4m=8m，将m的值看成函数y＝m2﹣4m与函数y=8m在第一象限内交点的横坐标，画出图象从而得出答案．
【解答】解：（1）作PD⊥OA于D，

∵∠AOB＝90°，
∴AB是直径，
∴PO＝PA，
∵OD＝AD，
∵P是反比例函数y=kx（k＞0，x＞0）图象上的动点，
∴OD×PD＝k，
∴S△POA＝k，
∵点P是AB的中点，
∴△OAB的面积为2S△POA＝2k；
（2）∵OP=12AB，
∴当OP最小时，AB的值最小，
当4x=x时，x＝2（负值舍去），
∴当P（2，2）时，OP最小为22，
∴AB的最小值为42；
（3）由（2）知，P（2，2），A（4，0），设C（m，4m），

过点C作CH⊥x轴于H，过点P作PG∥x轴，交CH于G，
∵∠ACP＝90°，
∴∠ACH+∠PCG＝90°，
∵∠ACH+∠CAH＝90°，
∴∠PCG＝∠CAH，
∵∠G＝∠AHC，
∴△PCG∽△CAH，
∴CGAH=PGCH，
∴2−4mm−4=m−24m，
化简得，m2﹣4m=8m，
将m的值看成函数y＝m2﹣4m与函数y=8m在第一象限内交点的横坐标，画出图象为：

∴m的近似值约为4.4，
∴点C横坐标的近似值约为4.4．