专题3.2 一次函数-2021年中考数学第一轮总复习课件（全国通用）

这是一份专题3.2 一次函数-2021年中考数学第一轮总复习课件（全国通用），共28页。PPT课件主要包含了＜m＜2，k＞0b＞0，k＞0b＜0，k＜0b＞0，k＜0b＜0，k1≠k2，k1·k2－1，yx＋b，－2＜x＜2，x-1等内容，欢迎下载使用。

考点1 一次函数的图象与性质
考点2 求一次函数的解析式
考点3 一次函数与方程(不等式)
考点4 一次函数的应用　
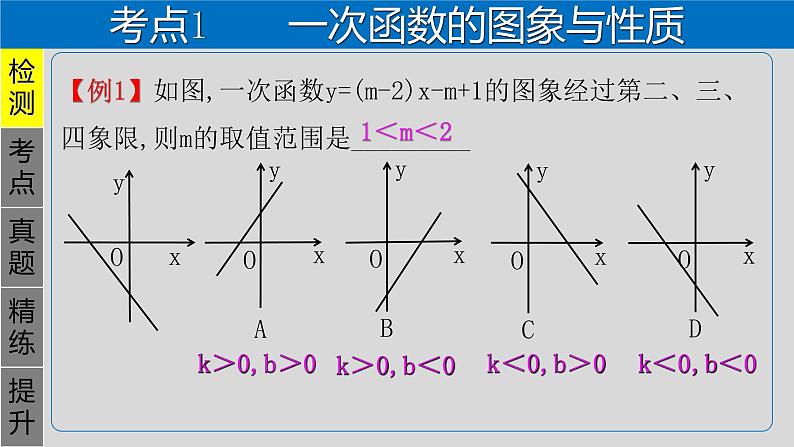
【例1】如图,一次函数y=(m-2)x-m+1的图象经过第二、三、四象限,则m的取值范围是_________
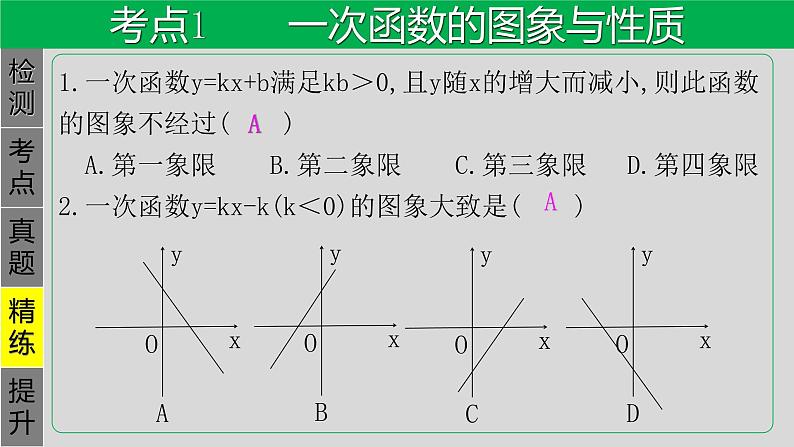
1.一次函数y=kx+b满足kb＞0,且y随x的增大而减小,则此函数的图象不经过(　　) A.第一象限 B.第二象限 C.第三象限 D.第四象限2.一次函数y=kx-k(k＜0)的图象大致是( )
3.一次函数y＝kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为(　　) A.(-5,3) B.(1，-3) C.(2,2) D.(5，-1)4.若点M(-7,m),N(-8,n)都在函数y=-(k2＋2k＋4)x＋1(k为常数)的图象上,则m和n的大小关系是(　　) A.m＞n B.m＜n C.m＝n D.不能确定5.一次函数y=-2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1＜x2,则y1____y2.(填“＞”“＜”“＝”)
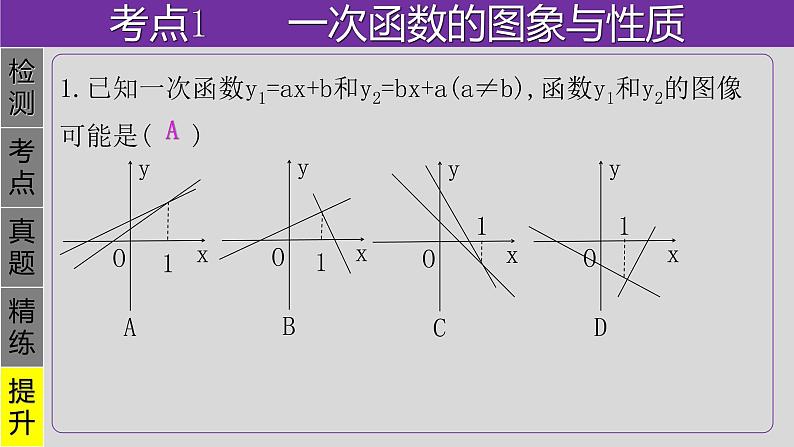
1.已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图像可能是( )
l1:y＝k1x＋b1和l2:y＝k2x＋b2的位置关系 1.平行⇔ 2.相交⇔ 3.垂直⇔
【例2】在平面直角坐标系中,将直线y=-2x＋1的图象向左平移2个单位,再向上平移1个单位,得到的直线的解析式是( 　) A.y=-2x-2　 B.y=-2x＋6 C.y=-2x-4 D.y=-2x＋4
k1＝k2，b1≠b2
【例3】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).(1)求直线AB的解析式；(2)若直线AB上的点C在第一象限,且S△BOC=2, 求点C的坐标．
【例4】已知一次函数y=kx＋2的图象与两坐标轴围成的三角形面积为2,求此一次函数的解析式．
1.(2016·T15)如图,过点A(2,0)的两条直线l1,l2分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=(1)求点B的坐标；(2)若△ABC的面积为4,求直线l2的解析式。
【考点】两条直线相交或平行问题；待定系数法求一次函数解析式；勾股定理的应用．
2.(2019·T17)如图,在平面直角坐标系中,点A,B的坐标分别为 ,连接AB,以AB为边向上作等边三角形ABC．(1)求点C的坐标；(2)求线段BC所在直线的解析式．
【考点】知识点：数形结合思想,转化思想与方程思想,计算能力；四基：几何推理,运算能力
3.(2020·T6)在平面直角坐标系中,点O为坐标原点,抛物线y=x2-2x-3与y轴交于点A,与x轴正半轴交于点B,连接AB,将Rt△OAB向右上方平移,得到Rt△O´A´B´,且点O´,A´落在抛物线的对称轴上,点B´落在抛物线上,则直线A´B´的表达式为( ) A.y=x B.y=x+1 C.y=x+0.5 D.y=x+2
1.将直线y=2x-3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( 　) A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-22.若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于( ) A.-1 B.0 C.3 D.43.将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为_____.
方法一：利用函数解析式求a的值；方法二：利用相似求a的值。
4.【教材母题】一个函数的图象是经过原点的直线,且这条直线过第四象限及点(2,-3a)与点(a,-6),求这个函数的解析式.
5.在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2)．(1)当-2＜x≤3时，求y的取值范围；(2)已知点P(m,n)在该函数的图象上,且m-n=4,求点P的坐标．
1.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( 　) A.5 B.4 C.3 D.22.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为6,则满足条件的直线l的条数是( 　) A.5 B.4 C.3 D.2
【例5】如图,直线y1=k1x+b1和y2=k2x+b2的图象如图所示,求下列方程(组)的解、不等式(组)的解集。 ①k1x+b1=0 ②k2x+b2=1 ③k1x+b1≤-2 ④k2x+b2＜4 ⑤k1x+b1＞k2x+b2
1.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b为(　) A.2 B.4 C.6 D.82.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线 y=-0.5x+b-1上,则常数b=(　 ) A.0.5 B.2 C.－1 D.13.一次函数y=-x-2与y=2x+m的图象相交于点P(n,-4),则关于x的不等式组 的解集为____________.
4.如图1,直线y=kx+b与y轴交于点(0,3)、与x轴交于点(a,0),当a满足-3≤a＜0时,k的取值范围是(　　) A.-1≤k＜0 B.1≤k≤3 C.k≥1 D.k≥35.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图2所示.根据图象信息可求得关于x的方程kx+b=0的解为______．
1.若函数y=kx+b的图象如图,则关于x的不等式k(x-3)+b＞0的解集为(　　) A.x＜2 B.x＜5 C.x＞2 D.x＞5【类比】我们知道方程x2+2x-3=0的解是x1=1,x2=-3,现给出另一个方程(2x+3)2+2(2x+3)-3=0,它的解是( ) A.x1=1,x2=3 B.x1=1,x2=-3 C.x1=-1,x2=3 D.x1=-1,x2=-3
利用一次函数进行方案选择
【例6】某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示：(1)填空：甲种收费方式的函数关系式是____________； 乙种收费方式的函数关系式是_________．(2)该校某年级每次需印制100≤x≤450 份学案,选择哪种印刷方式较合算？
利用一次函数解决分段函数问题
【例7】为响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的阶梯电价,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如折线图,请根据图象回答下列问题：(1)当用电量是180千瓦时时,电费是___元；(2)第二档的用电量范围是___________；(3)“基本电价”是___元/千瓦时；(4)小明家8月份的电费是328.5元,本月他家用电多少千瓦时?