



所属成套资源:2021年中考数学第一轮总复习课件(全国通用)
专题6.1 与圆有关的性质-2021年中考数学第一轮总复习课件(全国通用)
展开
这是一份专题6.1 与圆有关的性质-2021年中考数学第一轮总复习课件(全国通用),共27页。PPT课件主要包含了轴对称,平分弦所对的弧,º或105º,在同圆或等圆中,方法二角←→弧,圆心角的一半等内容,欢迎下载使用。
考点1 圆的有关概念
考点2 圆的性质与垂径定理
考点3 圆心角、弧、弦之间的关系
考点4 圆周角定理及推论
考点5 与圆有关的综合运用
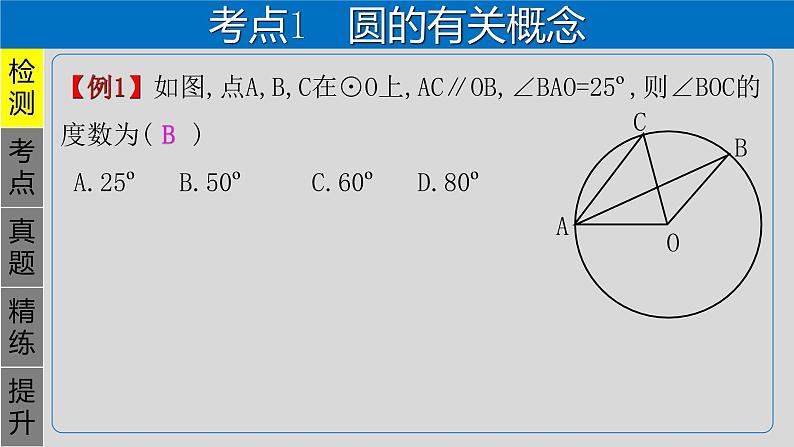
【例1】如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25º,则∠BOC的度数为( ) A.25º B.50º C.60º D.80º
1.圆的有关概念(1)圆:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆,其固定的端点O叫做圆心,线段OA叫做半径.(2)弧:圆上任意两点间的部分叫做圆弧,简称弧.(3)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.直径是圆内最长的弦.(4)等弧:在同圆或等圆中,能够互相_____的弧是等弧.(5)圆心角:顶点在圆心的角叫做圆心角.(6)圆周角:顶点在圆上,两边都与圆相交的角叫做圆周角.
2.圆的确定条件 圆心确定圆的位置,半径的确定圆的大小. (1)过一点和两点均可作无数个圆. (2)过不在同一直线上的三点确定一个圆,
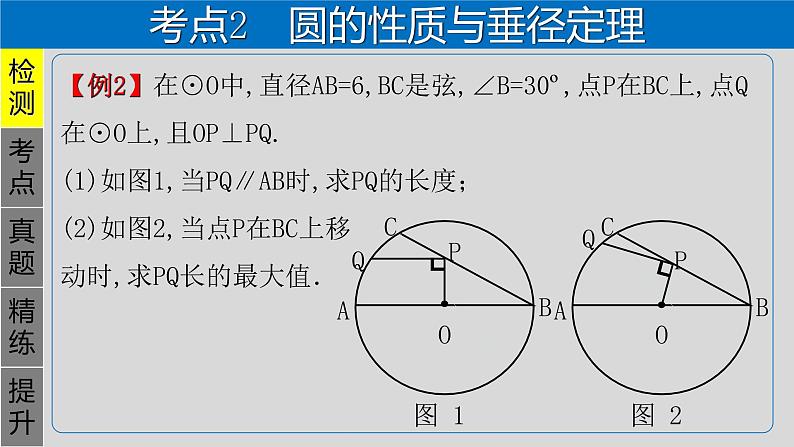
【例2】在⊙O中,直径AB=6,BC是弦,∠B=30º,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.
1.圆的性质(1)圆是_______图形;其对称轴是任意一条过_____的直线.(2)圆是______对称图形,对称中心为_____.(3)圆具有旋转不变性,即圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
2.垂径定理(1)垂径定理:_____于弦的直径_____这条弦,并且____弦所对的两条弧.(2)推论1:平分弦(不是直径)的直径_____于弦,并且_______________.(3)推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧. (4)推论3:平分弧的直径垂直平分弧所对的弦.
3.如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135º,则AB=_____.4.在半径为1的⊙O中,弦AB,AC的长分别为1和 ,则∠BAC的度数为___________.
1.如图,A,B,C,D为⊙O上四个点,若∠C=2∠ODB,∠ABD=70º,则∠ODB的度数为______.
(1)弧、弦、圆心角的关系:________________,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.(2)推论:在同圆或等圆中,如果两个圆心角,两条弧,两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都相等.
1.在同圆或等圆中,下列说法错误的是( ) A.相等弦所对的弧相等 B.相等弦所对的圆心角相等 C.相等圆心角所对的弧相等 D.相等圆心角所对的弦相等
【例4】如图,AB是半圆的直径,C,D是半圆上两点,∠ADC=106º,则∠CAB等于( ) A.10º B.14º C.16º D.26º
方法一:连接BD,∠CAB=∠CDB=∠ADC-∠ADB=106º-90º=16º
方法三:连接BC,利用圆内接四边形对角互补求∠CAB
1.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的______________2.推论:(1)半圆(直径)所对的圆周角是_____, 90º的圆周角所对的弦是_______; (2)在同圆或等圆中,相等的圆周角所对的弧相等.
3.圆内接四边形(1)定义:如果一个四边形的四个顶点在同一个圆上,那么这个四边形叫做这个圆的内接四边形,这个圆叫做四边形的外接圆.(2)性质:圆内接四边形的对角_____,任何一个外角都等于它的内对角.(3)判定:对角互补(或一边所对两个角相等)的四边形四个顶点共圆.4.四点共圆 (1)若四个点到一个定点的距离相等,则这四个点共圆; (2)对角互补(或外角等于它的内对角)的四边形四顶点共圆; (3)一边所对的两个角相等的四边形四顶点共圆.(定边对等角); (4)有公共斜边的两个直角三角形的顶点共圆, 且圆心为斜边的中点。
3.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50º,则∠DAC的大小为( ) A.130º B.100º C.65º D.50º4.如图,四边形ABCD内接于⊙O,若∠B=130º,则∠AOC的大小是( ) A.130º B.120º C.110º D.100º
5.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20º,则∠BCD的度数为( ) A.100º B.110º C.115º D.120º
方法一:角度转化为弧度;方法二:圆内接四边形对角互补。
【例5】如图,在⊙O位于直径AB的异侧有定点C和动点P,AC=0.5AB,点P在半圆弧AB上运动(不与A,B两点重合),过点C作直线PB的垂线CD交PB于D点.(1)如图①,求证:△PCD∽△ABC;(2)当点P运动到什么位置时,△PCD≌△ABC?请在图②中画出△PCD,并说明理由;(3)如图③,当点P运动到CP⊥AB时,求∠BCD的度数.
相关课件
这是一份专题6.1 与圆有关的性质-中考数学第一轮总复习课件,共24页。
这是一份专题6.3 与圆有关的计算-2023年中考数学第一轮总复习课件(全国通用),共22页。PPT课件主要包含了正多边形与圆,扇形的弧长与面积,圆锥的有关计算,外接圆的圆心,外接圆的半径,S侧πrl,π+2等内容,欢迎下载使用。
这是一份专题6.1 与圆有关的性质-2023年中考数学第一轮总复习课件(全国通用),共24页。PPT课件主要包含了圆的有关概念,圆的轴对称性,圆的旋转不变性,圆周角定理,圆内接四边形,另一个端点A,定点O,定长r,圆上任意两点间的部分,大于半圆等内容,欢迎下载使用。









