专题6.2 与圆有关的位置关系-2021年中考数学第一轮总复习课件（全国通用）

这是一份专题6.2 与圆有关的位置关系-2021年中考数学第一轮总复习课件（全国通用），共30页。PPT课件主要包含了考点4切线长定理，＜r＜5，点C在圆内，点A在圆外，点B在圆上，d＞r，d＝r，三边垂直平分线，三条角平分线等内容，欢迎下载使用。

考点 1 点与圆的位置关系
考点2 直线与圆的位置关系
考点3 圆的切线的性质及判定
考点5 三角形的内切圆、外接圆
【例1】在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是__________.
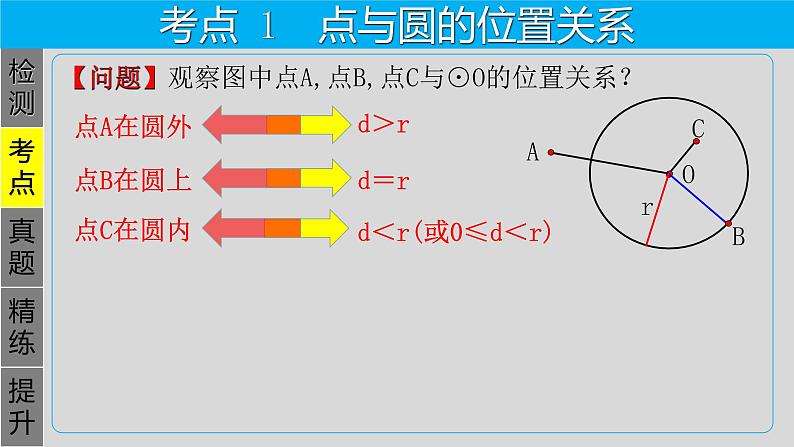
d＜r(或0≤d＜r)
【问题】观察图中点A,点B,点C与⊙O的位置关系？
1.一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是(　 ) 或7.5cm D.3cm或15cm2.在Rt△ABC中,∠C=90º,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为_______
【例2】Rt△ABC中,∠C=90º,AC=3cm,BC=4cm,以C为圆心,r为半径作圆,若⊙aC与直线AB相切,则r的值为(　　) A.2cm　 　　 　C.3cm　 　D.4cm
【问题】观察图中直线l1,直线l2,直线l3,与⊙O的位置关系？
【例3】如图,已知点E在Rt△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.(1)求证：AD平分∠BAC；(2)若BE=2,BD=4,求⊙O的半径．
“见切点,作垂直,得半径”。
【例4】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120º,连接PB.(1)求BC的长；(2)求证：PB是⊙O的切线．
(1)“有交点,作半径,证垂直”；(2)“无交点,作垂直,证半径”；
(2020·T21)已知∠MPN的两边分别与圆O相切于点A、B,圆O的半径为r.(1)如图1,点C在点A,B之间的优弧上,∠MPN=80º,求∠ACB的度数；(2)如图2,点C在圆上运动,当PC最大时,要使四边形APBC为菱形,∠APB的度数应为多少?请说明理由；(3)若PC交圆O于点D,求第(2)问中对应的阴影部分的周长(用含r的式子表示).
1.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接BC,若∠P=36º,则∠B等于(　　) A.27º B.32º C.36º D.54º
2.如图,AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( 　) A.4 B. C.3 D.2.5
【例5】如图,PA、PB分别切⊙O于A、B两点,连接PO、AB相交于D、C是⊙O上一点,∠C=60º.(1)求∠APB的大小；(2)若PO=20cm,求△AOB的面积．
1.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36º,则∠B等于(　) A.27º B.32º C.36º D.54º2.如图,AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( 　) A.4 B. C.3 D.2.5
3.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22º,则∠OCB=_____.
4.如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.求证：(1)DE⊥AE； (2)AE+CE=AB.
【例6】如图2,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是(　 ) A. B. C. D．
1.确定圆的条件:2.①外心：△ABC_______________的交点, ②∠BOC=2∠BAC3.①内心：△ABC_____________的交点, ②∠BIC=90º+0.5∠BAC
不在同一直线的三个点确定一个圆
1.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________2.如图,在△ABC中,∠A=66º,点I是内心,则∠BIC的大小为( ) A.114° B.122° C.123° D.132° 3.如图为4×4的网格图,A,B,C,D,O均在格点上,点O是(　　)A.△ACD的外心 B.△ABC的外心 C.△ACD的内心 D.△ABC的内心
6.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D、E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( 　) A.r C.2r
(2016·T18)如图,AB是⊙O的直径,点P是弦AC上一动点(不与A、C重合),过点P作PE⊥AB,垂足为E,射线EP交AC于点F,交过点C的切线于点D.(1)求证:DC=DP(2)若∠CAB=30º,当F是AC的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由；
(2017·T21)如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30º,过点P作PD⊥OP交⊙O于点D．(1)如图2,当PD∥AB时,求PD的长；(2)如图3,当DC=AC时,延长AB至点E,使BE=0.5AB,连接DE．①求证：DE是⊙O的切线；②求PC的长．
(2018·T20)如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C，过点A作AD⊥BO交BO的廷长线于点D,且∠AOD=∠BAD．(1)求证：AB为⊙O的切线；(2)若BC=6,tan∠ABC= ,求AD的长．
(2019·T19)如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线，过半圆上的点C作CD∥AB交AF于点D，连接BC．(1)连接DO,若BC∥OD,求证：CD是半圆的切线；(2)如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论．