考点24-2 图形的翻折-2022年中考数学专项分类提分训练（天津专用）

考点24—2图形的翻折

1．如图1，在平面直角坐标系中有长方形OABC，点，将长方形OABC沿AC折叠，使得点B落在点D处，CD边交x轴于点E，．

（1）求点D的坐标；

（2）如图2，在直线AC以及y轴上是否分别存在点M，N，使得△EMN的周长最小？如果存在，求出△EMN周长的最小值；如果不存在，请说明理由；

（3）点P为y轴上一动点，作直线AP交直线CD于点Q，是否存在点P使得△CPQ为等腰三角形？如果存在，请求出∠OAP的度数；如果不存在，请说明理由．

2．等边的边长为，是边上任一点（与不重合），连接，以为边向两侧作等边和等边，分别与边交于点（如图1）

（1）求证：；

（2）若，求四边形与重叠部分的面积；

（3）连接，分别与边交于点（如图2），当时，求的长，判断此时以这三条线段为边构成的三角形是什么特殊三角形，并说明理由．

3．在矩形ABCD中，将矩形折叠，使点B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于点F（如图1和图2），然后展开铺平，连接BE，EF．

（1）操作发现：

①在矩形ABCD中，任意折叠所得的△BEF是一个　   　三角形；

②当折痕经过点A时，BE与AE的数量关系为　   　．

（2）深入探究：

在矩形ABCD中，AB＝，BC＝2．

①当△BEF是等边三角形时，求出BF的长；

②△BEF的面积是否存在最大值，若存在，求出此时EF的长；若不存在，请说明理由．

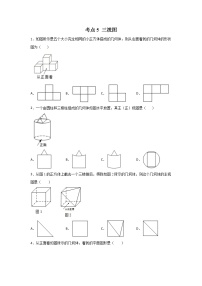
4．将长方形纸片，按下列要求折叠．并回答问题1，2，3；

（折叠一）

第1步：将长方形纸片，按图1所示的方法折叠；

第2步：按图2所示的方法折叠；

第3步：将图形展开，如图3，在长方形ABCD中，EF，GD为折叠过程中产生的折痕

问题1：EF与GD平行？请说明理由．

（折叠二）

第1步：将长方形纸片，按图4所示的方法折叠；

第2步：按图5所示的方法折叠；

第3步：将图形展开，如图6，将长方形ABCD中，EF，GH为折叠过程中产生的折痕．

问题2：EF与GH平行吗？请说明理由．

问题3：如图7，在（折叠二）中，若纸片的长为16厘米，宽为2厘米，则阴影部分面积的最大值为＿＿＿＿＿＿＿＿．

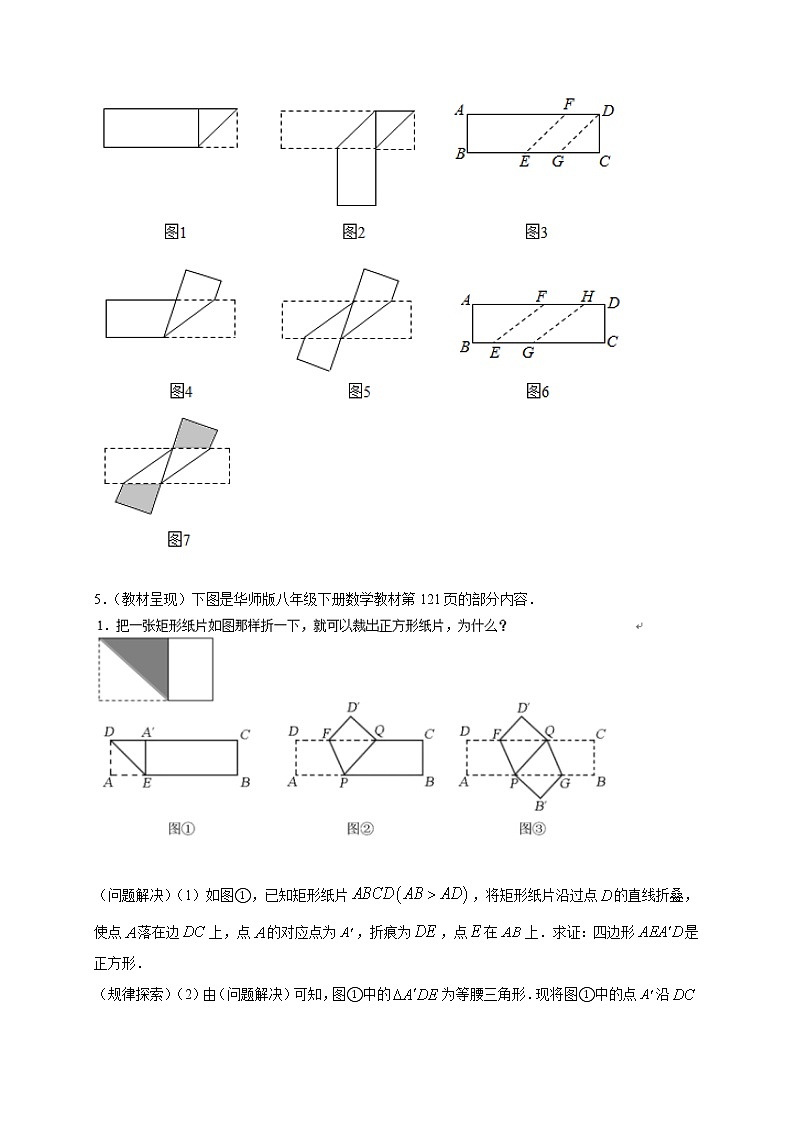
5．（教材呈现）下图是华师版八年级下册数学教材第121页的部分内容．

（问题解决）（1）如图①，已知矩形纸片，将矩形纸片沿过点的直线折叠，使点落在边上，点的对应点为，折痕为，点在上．求证：四边形是正方形．

（规律探索）（2）由（问题解决）可知，图①中的为等腰三角形．现将图①中的点沿向右平移至点处（点在点的左侧），如图②，折痕为，点在上，点在上，那么还是等腰三角形吗？请说明理由．

（结论应用）（3）在图②中，当时，将矩形纸片继续折叠如图③，使点与点重合，折痕为，点在上．要使四边形为菱形，则___________．

6．如图，在矩形中，，点是边上的一个动点，将四边形沿直线折叠，得到四边形，点、的对应点分别为点、．直线交于点．

（1）求证：；

（2）连接，已知．

①如图①，当，时，求的长度；

②如图②，当四边形为菱形时，请直接写出的长度．

图①                                图②

7．如图，在矩形ABCD中，AB=10，BC=m，E为BC边上一点，沿AE翻折△ABE，点B落在点F处．

（1）连接CF，若CF//AE，求EC的长（用含m的代数式表示）；

（2）若EC=，当点F落在矩形ABCD的边上时，求m的值；

（3）连接DF，在BC边上是否存在两个不同位置的点E，使得？若存在，直接写出m的取值范围；若不存在，说明理由．

8．如图，在平面直角坐标系中，矩形的顶点O与坐标原点重合，顶点A、C在坐标轴上，，将矩形沿折叠，使点A与点C重合．

（1）求点E的坐标；
（2）点P从O出发，沿折线方向以每秒2个单位的速度匀速运动，到达终点E时停止运动，设P的运动时间为t，的面积为S，求S与t的关系式，直接写出t的取值范围；
（3）在（2）的条件下，当时，在平面直角坐标系中是否存在点Q，使得以点P、E、G、Q为顶点的四边形为平行四边形？若不存在，请说明理由；若存在，请求出点Q的坐标．

9．（1）、动手操作：

如图①：将矩形纸片ABCD折叠，使点D与点B重合，点C落在点处，折痕为EF，若∠ABE＝20°，那么的度数为        .

（2）、观察发现：

小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．

（3）、实践与运用：

将矩形纸片ABCD按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP＝MN＝PQ（如图④），求∠MNF的大小.

10．如图，在矩形中，点是上的一点（不与点，重合），沿折叠，得，点的对称点为点．

（1）当时，点会落在上吗？请说明理由．

（2）设，且点恰好落在上．

①求证：．

②若，用等式表示的关系．

11．如图，在矩形中，，点E是边上的动点，将矩形沿折叠，点A落在点处，连接.

（1）如图，求证：；

（2）如图，若点恰好落在上，求的值；

（3）点E在边上运动的过程中，的度数是否存在最大值，若存在，求出此时线段的长；若不存在，请说明理由.

12．如图1，已知矩形纸片ABCD中，AB＝6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．

（1）求矩形ABCD的边AD的长．

（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP＝x cm，DM＝y cm，试求y与x的函数关系式，并指出自变量x的取值范围．

（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；

②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式

13．如图，已知一个直角三角形纸片ACB，其中∠ACB＝90°，AC＝4，BC＝3，E、F分别是AC、AB边上点，连接EF，将纸片ACB的一角沿EF折叠．

（1）如图①，若折叠后点A落在AB边上的点D处，且使S四边形ECBF＝3S△AEF，则AE＝    ；

（2）如图②，若折叠后点A落在BC边上的点M处，且使MF∥CA．求AE的长；

（3）如图③，若折叠后点A落在BC延长线上的点N处，且使NF⊥AB．求AE的长．

14．如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）

（1）用这样的两个三角形构造成如图（2）的图形，利用这个图形，证明：a2+b2＝c2；

（2）用这样的两个三角形构造图3的图形，你能利用这个图形证明出题（1）的结论吗？如果能，请写出证明过程；

（3）当a＝3，b＝4时，将其中一个直角三角形放入平面直角坐标系中，使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合（如图4中Rt△AOB的位置）．点C为线段OA上一点，将△ABC沿着直线BC翻折，点A恰好落在x轴上的D处．

①请写出C、D两点的坐标；

②若△CMD为等腰三角形，点M在x轴上，请直接写出符合条件的所有点M的坐标．

15．实践操作：在矩形ABCD中，AB＝4，AD＝3，现将纸片折叠，点D的对应点记为点P，折痕为EF（点E、F是折痕与矩形的边的交点），再将纸片还原．

初步思考：

（1）若点P落在矩形ABCD的边AB上（如图①）

①当点P与点A重合时，∠DEF＝　   　°；当点E与点A重合时，∠DEF＝　   　°；

②当点E在AB上，点F在DC上时（如图②），

求证：四边形DEPF为菱形，并直接写出当AP＝3.5时的菱形EPFD的边长．

深入探究

（2）若点P落在矩形ABCD的内部（如图③），且点E、F分别在AD、DC边上，请直接写出AP的最小值　   　．

拓展延伸

（3）若点F与点C重合，点E在AD上，线段BA与线段FP交于点M（如图④）．在各种不同的折叠位置中，是否存在某一情况，使得线段AM与线段DE的长度相等？若存在，请直接写出线段AE的长度；若不存在，请说明理由．

16．如图1，已知的边平行于轴，点的坐标为，点的坐标为，点在第四象限，点是边上的一个动点．

（1）若点在边上，求点的坐标；

（2）若点在边或上，点是与轴的交点如图2，过点作轴的平行线过点作轴的平行线它们相交于点，将沿直线翻折，当点的对应点落在坐标轴上时，求点的坐标．(直接写出答案)

17．在中，，点是边的中点，动点在边上(点不与点重合)，连接，将沿直线翻折，点落在点处得．

（1）如图①，若点恰好与点重合，求线段的长；

（2）如图②，若交于点，四边形为菱形，求证：；

（3）连接与重叠部分的面积为的面积为，若时，请直接写出的值．

18．再读教材：宽与长的比是(约为0.618)的矩形叫作黄金矩形．黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计．下面，我们用宽为2的矩形纸片折叠黄金矩形(提示：)．

第一步：在矩形纸片一端 ，利用图1的方法折出一个正方形，然后把纸片展平；

第二步：如图2，把这个正方形折成两个相等的矩形，再把纸片展平；

        图1                  图2

第三步：折出内侧矩形的对角线，并把折到图3中所示的处；

第四步：展平纸片，按照所得的点折出，使，则图4中就会出现黄金矩形．

         图3                图4

(1)在图3中_________ (保留根号)；

(2)如图3，则四边形的形状是_________；

(3)在图4中黄金矩形是_________．

19．如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到到B′的位置，AB′与CD交于点E.

（1）求证：△AED≌△CEB′

（2）若AB = 8，DE = 3，点P为线段AC上任意一点，PG⊥AE于G，PH⊥BC于H.求PG + PH的值.

20．取一张矩形纸片进行折叠，具体操作过程如下：第一步：先把矩形ABCD对折，折痕为MN，如图1；第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B'，得Rt△AB'E，如图2；第三步：沿EB'线折叠得折痕EF，使A点落在EC的延长线上，如图3．　　

利用展开图4探究：  

（1）△AEF是什么三角形?证明你的结论；

（2）对于任一矩形，按照上述方法是否都能折出这种三角形?请说明理由．

21．如图，矩形纸片ABCD中，AB=，BC=．某课题小组利用这张矩形纸片依次进行如下操作（每次折叠后均展开）．

如图①，第一次将纸片折叠，使点B与点D重合，折痕与BD交于点O1，设O1D的中点为D1；

如图②，第二次将纸片折叠，使点B与点D1重合，折痕与BD交于点O2，设O2D3的中点为D2；

如图③，第三次将纸片折叠，使点B与点D2重合，折痕与BD交于点O3，设O3D2的中点为D3；

…

根据以上操作结果，回答下列问题：

（1）如图①，MN是折痕，求证：△DA′M≌△DCN；

（2）分别求出线段BO1、BO2、BO3的长，并直接写出第n次折叠后BOn的长（用含n的式子表示）；

（3）如图②，第二次折叠时，折痕一定会经过点A吗？请通过计算判断．

22．如图，在平面直角坐标系中，矩形OABC的顶点O是坐标原点，OA、OC分别在x轴、y轴的正半轴上，且OA＝5，OC＝4．

(1)如图①，将矩形沿对角线OB折叠，使得点A落在点D处，OD与CB相交于点E，请问重叠部分△OBE是什么三角形？说明你的理由：并求出这个三角形的面积；

(2)如图②，点E、F分别是OC、OA边上的点，将△OEF沿EF折叠，使得点O正好落在BC边上的D点，过点D作DH⊥OA，交EF于点G，交OA于点H，若CD＝2，求点G的坐标；

(3)如图③，照(2)中条件，当点E、F在OC、OA上移动时，点D也在边BC上随之移动，请直接写出BD的取值范围．

23．如图1，在矩形纸片ABCD中，AB＝12cm，AD＝20cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．

（1）求证：四边形BFEP为菱形；

（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；

①当点Q与点C重合时（如图2），求菱形BFEP的边长；

②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．

24．如图，四边形是一张矩形纸片，，把纸片对折，折痕为，展开后再过点折叠该纸片，使点落在上的点处，且折痕与相交于点，再次展平后，连接，，并延长交于点．

（1）求证：是等边三角形；

（2）求，的长；

（3）为线段上一动点，是的中点，则的最小值是　　　　．（请直接写出结果）

25．对一张矩形纸片进行折叠，具体操作如下：

第一步：先对折，使与重合，得到折痕，展开；

第二步：再一次折叠，使点落在上的点处，并使折痕经过点，得到折痕，同时，得到线段，，展开，如图①；

第三步：再沿所在的直线折叠，点落在上的点处，得到折痕，同时得到线段，展开，如图②.

（1）求证：

（2）求证：四边形为菱形.

26．如图，在矩形ABCD中，AB=4，AD=6，E是AD边上的一个动点，将四边形BCDE沿直线BE折叠，得到四边形BC′D′E，连接AC′，AD′.

（1）若直线DA交BC′于点F，求证：EF=BF；

（2）当AE=时，求证：△AC′D′是等腰三角形；

（3）在点E的运动过程中，求△AC′D′面积的最小值．

27．如图①，在矩形纸片ABCD中，AB=4，AD=6．点E，F分别在AB，DC上（E不与A，D重合，F不与B，C重合），现以EF为折痕，将矩形纸片ABCD折叠．

（1）当A点落在BC上时（如图②），求证：△EFA′是等腰三角形；

（2）当A′点与C重合时，试求△EFA’的面积；

（3）当A′点与DC的中点重合时，试求折痕EF的长．

28．已知长方形中，，点在边上，由往运动，速度为，运动时间为秒，将沿着翻折至，点对应点为，所在直线与边交于点，

（1）如图，当时，求证：；

（2）如图，当为何值时，点恰好落在边上；

（3）如图，当时，求的长.

29．如图，平面直角坐标系中，四边形OABC是长方形，O为原点，点A在x轴上，点C在y轴上且A（10，0），C（0，6），点D在AB边上，将△CBD沿CD翻折，点B恰好落在OA边上点E处． 

（1）求点E的坐标；   

（2）求折痕CD所在直线的函数表达式；   

（3）请你延长直线CD交x轴于点F．  ①求△COF的面积；

②在x轴上是否存在点P，使S△OCP=S△COF？若存在，求出点P的坐标；若不存在，请说明理由．

30．（问题情境）如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

小丽给出的提示是：如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．

请根据小丽的提示进行证明．

（变式探究）如图③，当点P在BC延长线上时，其余条件不变，试猜想PD、PE、CF三者之间的数量关系并证明．

（结论运用）如图④，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值．