人教版九年级上册第二十二章 二次函数综合与测试教学课件ppt

这是一份人教版九年级上册第二十二章 二次函数综合与测试教学课件ppt，共23页。PPT课件主要包含了二次函数与实际问题，a＞0，a＜0，yax2+bx+c，没有实数根，x＜x1或x＞x2，x≠x1的一切实数，所有实数，x1＜x＜x2，m≤5等内容，欢迎下载使用。

二次函数的图象及性质
二次函数与一元二次方程
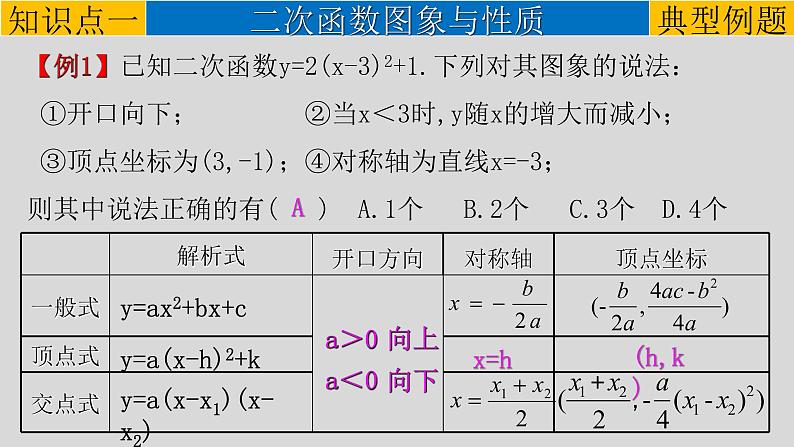
【例1】已知二次函数y=2(x-3)2+1.下列对其图象的说法： ①开口向下； ②当x＜3时,y随x的增大而减小； ③顶点坐标为(3,-1)；④对称轴为直线x=-3；则其中说法正确的有( 　) A.1个 B.2个 C.3个　D.4个
y=a(x-h)2+k
y=a(x-x1)(x-x2)
1.对于y=2(x-3)2+2的图像下列叙述正确的是(　　)A.顶点坐标为(-3,2) B.当x≥3时,y随x的增大而增大 C.对称轴为y＝3 D.当x≥3时,y随x的增大而减小2.抛物线y=a(x+3)(x-1)的对称轴是直线( 　)　A.x=1 B.x=-1　　C.x=-3 D.x=33.下列对二次函数y＝x2-x的图象的描述,正确的是(　　) A.开口向下 B.对称轴是y轴 C.经过原点 D.在对称轴右侧部分是下降的
4.若点A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=(x+1)2+k的图象上的三点,则y1、y2、y3的大小关系是( ) A.y1＜y2＜y3 B.y2＜y1＜y3 C.y3＜y1＜y2 D.y1＜y3＜y25.若抛物线y=-x2+bx+c经过点(-2,3),则2c-4b-9的值是(　　) A.5 B.-1 C.4 D.186.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下：则该函数图象的对称轴是(　) A.直线x=-3 B.直线x=-2 C.直线x=-1 D.直线x=0
7.抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( ) A.m＞1 B.m＞0 C.m＞-1 D.-1＜m＜08.已知二次函数y=ax2-2ax-3a(a≠0),关于此函数的图象及性质,下列结论中不一定成立的是( ) A.该图象的顶点坐标为(1,-4a)； B.该图象与x轴的交点为(-1,0),(3,0)； C.若该图象经过点(-2,5),则一定经过点(4,5)； D.当x＞1时,y随x的增大而增大。
1.已知抛物线y=-(x+1)2+k的图像上有A(-2,y1),B(1,y2),C(2,y3)三点,则y1,y2,y3的大小关系是( ) A.y1＞y2＞y3 B.y1＞y3＞y2 C.y3＞y2＞y1 D.y3＞y1＞y22.已知二次函数y=x2-2x-3,当0≤x≤3时,y的最大值和最小值分别是( ) A.0，-4 B.0，-3 C.-3，-4 D.0，03.已知抛物线y=x2-8x+c的顶点在x轴上,则c=＿＿.
4.把抛物线y=-x2沿着x轴方向平移3个单位长度，那么平移后抛物线的解析式是 .5.如果一条抛物线的形状与 形状相同,且顶点坐标是(4,-2),则这个函数关系式为___________________________.6.抛物线y=(m+1)xm2-m+3,当x＞0时y随x的增大而增大,则m=___.7.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则a=____.8.抛物线y=ax2+c与x轴交于A(-2,0),B两点,与y轴交于点C(0,-4),则三角形ABC的面积是___.
y=-(x+3)2或y=-(x-3)2
【例4】已知二次函数y=x2-3x+m的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是(　 ) A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
有两个不等的实数根x1,x2
x1=x2=-b/2a
1.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c-8=0的根的情况是( ) A.有两个不相等的正实数根 B.没有实数根 C.有两个相等的实数根 D.有两个异号实数根2.函数y=ax2+2ax+m(a＜0)的图象过点(2,0),则使函数值y＜0成立的x的取值范围是(　　) A.x＜-4或x＞2 B.-4＜x＜2 C.x＜0或x＞2 D.0＜x＜2
x1=-1,x2=3　　
【变式1】小丽跳绳时,发现在绳子运动到最高点时,绳子可以看做是一条抛物线,此时测得两手柄外端之间的距离AB=1米,手柄离地面的距离为1.2米,小丽的头顶离地面的距离为1.95米,绳子在小丽头顶同高度的C,D处相距0.5米。则绳子的最高点离地面的距离为______米.
【解析】如图建立平面直角坐标系， 则可求得抛物线的解析式为y=-4x2+1， ∴顶点E的坐标为(0,1)， ∴绳子的最高点离地面的距离为2.2米。
2.二次函数y=ax2+bx+c的图象如图所示,则函数值y＜0时,x的取值范围是( 　) A.x＜-1 B.x＞3 C.-1＜x＜3 D.x＜-1或x＞3
18.若抛物线y=x2+bx+c的顶点在第一象限,则方程 x2+bx+c=0的根的情况是＿＿＿＿＿.19.一元二次方程3x2+x-10=0的两个根是x1=-2,x2=5/3,那么二次函数y=3x2+x-10与x轴的交点坐标是________________.20.若二次函数y=-x2+2x+k的部分图象如图,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2= ；
(-2,0),(5/3,0)
【例3】2020年1月新型冠状病毒爆发,全国各地在党和政府的领导和组织下,有效的遏制了病情的蔓延.戴口罩在防止病毒的蔓延起到的重要作用.小明发现,一次性口罩的形状和他学习的抛物线相似,建立如图所示的平面直角坐标系,口罩的下边沿可以用抛物线y1=x2-1表示,它的顶点为P,交x轴于点C,D.口罩的上边沿可以看成把口罩的下边沿向上平移后得到的,使顶点落在x轴上,A,B分别为C,D的对应点.求口罩的面积S(阴影部分)．
解：连接AB,当y=0时,0=x2-1,∴x=±1∴C、D两点的坐标分别为(-1,0),(1,0),则CD=2.∴由抛物线平移的性质可知：抛物线PCD与线段CD围成的面积等于抛物线OAB与线段AB围成的面积∴S=S矩形ABDC=CD×AC=2×1=2
【变式】小明发现,N95型口罩的上、下边沿是对称的抛物线,左、右边沿可以看成两条线段AC=BD=1,建立如图所示的平面直角坐标系,口罩的下边沿可以看成抛物线y1=x2-1,求口罩的上边沿的抛物线的解析式．
解：由y1=x2-1可得顶点P的坐标为(0,-1)∴OP=1, 连接AB交y轴于点E, 由轴对称的性质可知QE=OP=1,OE=AC=BD=1,∴点Q的坐标为(0,2)∵抛物线AQB与抛物线CPD对称∴抛物线AQB的解析式为： y2=-x2+2
…………………… 6分
1.如图,在平面直角坐标系中,抛物线y=0.5x2经过平移得到抛物线y=0.5x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为( ) A.2 　 B.4　 C.8　 D.162.如图,边长为2的正方形ABCD的中心在平面直角坐标系的原点O处,AD∥x轴,以O为顶点且过A,D两点的抛物线与以O为顶点且过B,C两点的抛物线将正方形分割成几部分,则图中阴影部分的面积是____.
3.如图,二次函数y1=-x2+2图象向右平移1个单位得到的y2.回答下列问题：(1)y2图象的顶点坐标 ．(2)图中阴影部分的面积___．(3)若再将y2绕原点O旋转180º得到y3,则y3的开口方向 ,顶点坐标 .