数学九年级上册第二十三章 旋转综合与测试教学课件ppt

这是一份数学九年级上册第二十三章 旋转综合与测试教学课件ppt，共19页。PPT课件主要包含了小角全在大角内部，思路点拨，强化训练，拓展提升等内容，欢迎下载使用。

1.半角模型:把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型.2.常见的图形:正方形、正三角形、等腰直角三角形等。3.解题思路: ①将半角两边的三角形通过旋转到一边合并形成新的三角形； ②证明一对轴对称的全等三角形； ③通过全等的性质得出线段之间的数量关系,从而解决问题.
半角信息——带形旋转——轴对称的全等三角形
小角不全在大角内部
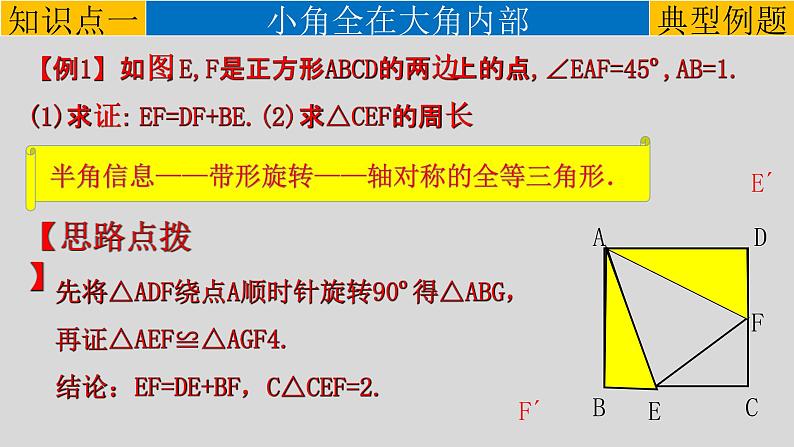
【例1】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,AB=1.(1)求证：EF=DF+BE.(2)求△CEF的周长
先将△ADF绕点A顺时针旋转90º得△ABG，再证△AEF≌△AGF4.结论：EF=DE+BF，C△CEF=2.
半角信息——带形旋转——轴对称的全等三角形．
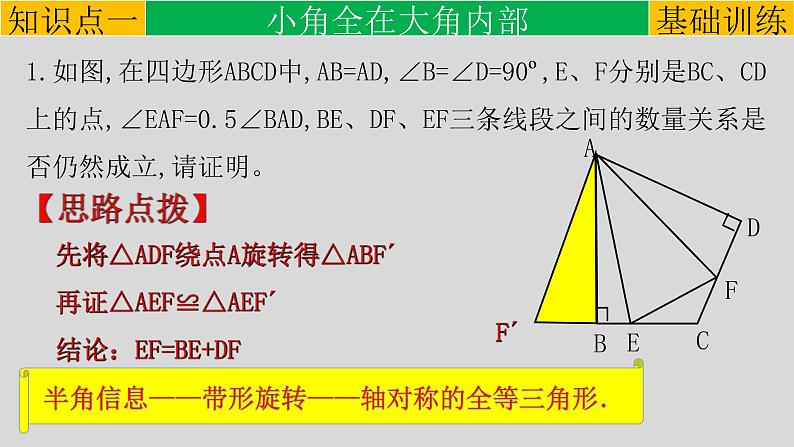
1.如图,在四边形ABCD中,AB=AD,∠B=∠D=90º,E、F分别是BC、CD上的点,∠EAF=0.5∠BAD,BE、DF、EF三条线段之间的数量关系是否仍然成立,请证明。
先将△ADF绕点A旋转得△ABF´再证△AEF≌△AEF´结论：EF=BE+DF
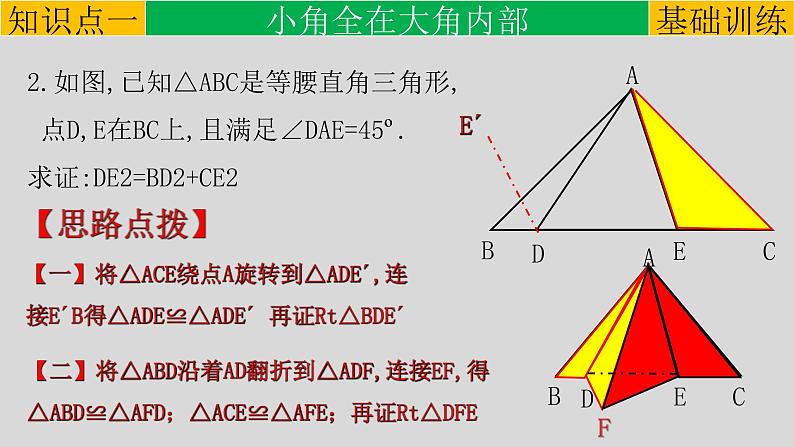
【一】将△ACE绕点A旋转到△ADE´,连接E´B得△ADE≌△ADE´ 再证Rt△BDE´
2.如图,已知△ABC是等腰直角三角形, 点D,E在BC上,且满足∠DAE=45º.求证:DE2=BD2+CE2
【二】将△ABD沿着AD翻折到△ADF,连接EF,得△ABD≌△AFD；△ACE≌△AFE；再证Rt△DFE
1.如图,在四边形ABCD中,AB=AD=CD=4,AD∥BC,∠B=60º,点E、F分别为边BC、CD上两个动点,且∠EAF=60º,则△AEF的面积是否存在最小值?若存在,求出其最小值；若不存在,请说明理由.
【简答】将△ADF绕点A顺时针旋转120º,得△ABF´,则∠EAF´=60º,易证△AEF´≌△AEF,作△AEF´的外接圆⊙O,作OH⊥BC于点H,AG⊥BC于点G,则∠F´OH=60º,设⊙O的半径为r,则OH=0.5OF=0.5r.∵OA+OH≥AG,
2.点E在边长为4的正方形ABCD的边BC上,点F在边CD上,∠EAF=45º,则△AEF面积的最小值为________.
条件：①正方形ABCD；②∠EAF=45º；
结论：①EF=DF-BE；
先将△ABE绕点A旋转得△ADE´再证△AEF≌△AE´F结论：EF=BE-DF
1.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180º,E,F分别是BC，CD上的点,且∠EAF=0.5∠BAD,BE,DF,EF三条线段之间的数量关系是否仍然成立,若不成立,写出它们之间的数量关系并证明.
1.如图,在四边形ABCD中,AB=AD,∠B+∠D=180º,E、F分别是BC、CD上的点,且∠EAF=0.5∠BAD,BE、DF、EF三条线段之间的数量关系是否仍然成立,请证明。
先将△ABE绕点A旋转得△ADE´再证△AEF≌△AE´F´结论：EF=BE+DF
2.如图,已知四边形ABCD是正方形,对角线AC,BD相交于O.设E,F分别是AB上不同的两个点,且∠EOF=45º,请你用等式表示线段AE,BF和EF之间的数量关系,并证明．
【思路点拨】1.先将△OFB绕点O顺时针旋转90º得△F´OA，2.再由△EOF´≌△EOF(SAS)得EH=EF.3.利用勾股定理得F´E2=F´A2＋AE2，4.∴EF2=F´A2＋AE2，
3.如图所示,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=120º的等腰三角形,以D为顶点作一角等于60º.角的两边分别交AB、AC于M、N,连接MN,构成一个△AMN,求△AMN的周长.
【思路点拨】1.先将△DBM绕点D顺时针旋转120º得△DCE2.再证△DMN≌△DEN3.C△AMN=AM＋MN＋AN=AM＋NE＋AN =AM＋CE＋NC＋AN=(AM＋MB)＋(NC＋AN) =AB＋AC=2
4.如图,在正方形ABCD内作∠EAF=45º,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.(1)将△ADF绕点A顺时针旋转90º得到△ABG． 求证:△AGE≌△AFE;(2)若BE=2,DF=3,求AH的长．(3)如图,连接BD交AE于点M,交AF于点N.探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
(2)由勾股定理得:EF2=FC2+EC2,求得AH=AB=6(3)先将△ABM逆时针旋转90º得△ADM´,连接M´N再证△AMN≌△AM´N(SAS)由勾股定理得：M´N2=ND2+M´D2 ∴BM2+ND2=MN2
5.如图,已知在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD´,连接D´E.(1)当∠BAC=120º时,∠DAE=60º时,求证:DE=D´E；(2)当DE=D´E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.(3)在(2)的结论下,当∠BAC=90º,BD与DE满足怎样的数量关系时,△D´EC是等腰直角三角形?(直接写出结论,不必证明)
(1)证△ADE≌△AD´E(SAS)得DE=D´E (2)证△ADE≌△AD´E(SSS)得∠D´AE=∠DAE,再得∠DAE=0.5∠BAC.(3)由旋转的性质得BD=CD´,DE=D´E,∠ACD´=∠B=45º由△D´EC是等腰直角三角形得：D´E= CD´,DE= BD.
1.如图,在四边形ABCD中,AD∥BC，∠BCD=90º,AB=BC+AD,∠DAC=45º,E是CD上一点，且∠BAE=45º,若CD=4,则△ABE的面积为____.
【思路点拨】1.将△ADE绕点A逆时针旋转90º。2.设BC=a,在Rt△ABF中求出a=1.3.设BE=b,利用半角模型得出BG=BE=b, ∴DE=GF=b-3,CE=7-b.4.在Rt△BCE中求出b=25/7