数学九年级上册第二十三章 旋转综合与测试教学课件ppt

这是一份数学九年级上册第二十三章 旋转综合与测试教学课件ppt，共23页。PPT课件主要包含了①旋转的目的，②旋转的条件，③旋转的方法，等腰三角形，等边三角形，等腰直角三角形，正方形，利用旋转求角的大小，利用旋转求线段的长度，思路点拨等内容，欢迎下载使用。
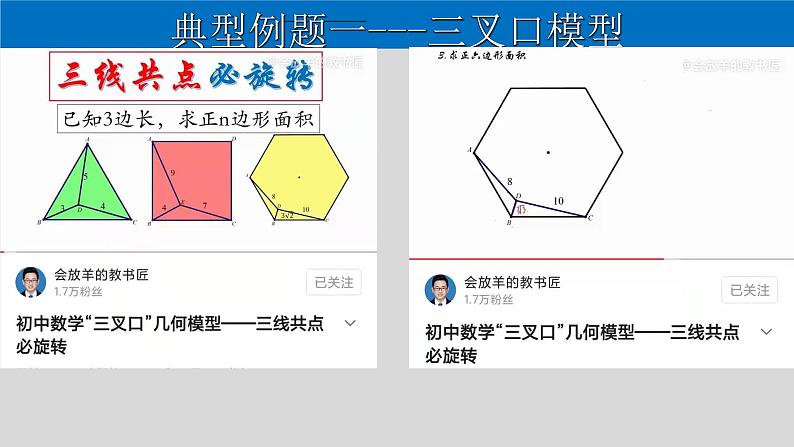
典型例题一---三叉口模型
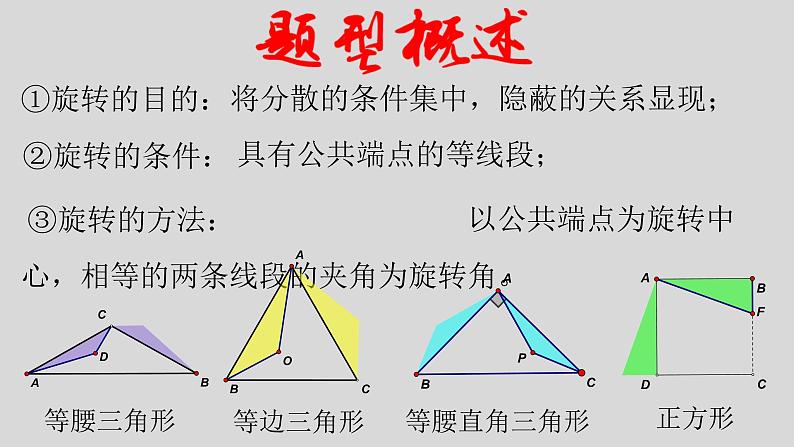
以公共端点为旋转中心，相等的两条线段的夹角为旋转角。
将分散的条件集中，隐蔽的关系显现；
具有公共端点的等线段；
利用旋转线段之间的关系
【例1】如图,点P为等边△ABC内一点,且PA=4,PB=3,PC=5, 求∠APB的度数．
3.∠APB=∠BQC=∠BQP+∠PQC =60º+90º=150º
1.先将△ABP绕点B顺时针旋转60º 得△CBQ,再连接PQ
2.再证△CBQ是正三角形, △CPQ 是直角三角形
1.已知在△ACB中,∠ACB=90º,AC=BC,PA=3,PC=2,PB=1, 求∠BPC的度数？
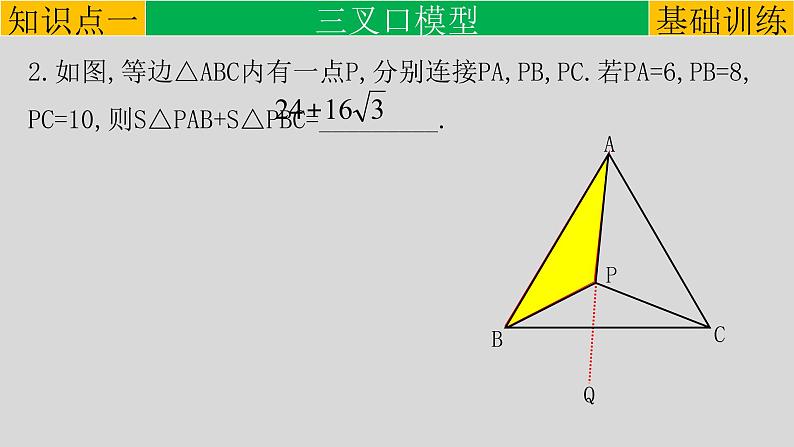
2.如图,等边△ABC内有一点P,分别连接PA,PB,PC.若PA=6,PB=8,PC=10,则S△PAB+S△PBC=_________.
【例2】如图,点P是等边△ABC内一点,PB=2,PC=1,∠BPC=150º, 求PA的长．
【问题提出】如图1,在等边△ABC内部有一点P,PA=3,PB=4,PC=5.求∠APB的度数.【数字思考】当图形中有一组邻边相等时,通过旋转可以将分散的条件集中起来解决问题.【尝试解决】将△APC绕点A逆时针旋转60º,得到△AP´B,连接P´P,则△APP´为等边三角形,∵P´P=PA=3,PB=4,P´B=PC=5,∴P´P2+PB2=P´B2,△BP´P为______三角形.∴∠APB的度数为_____.【类比探究】如图2,在等边△ABC外部有一点P,若∠BPA=30º,求证：PA2+PB2=PC2；【联想拓展】如图3,在△ABC中,∠BAC=90º,AB=AC.点P在直线BC上方且∠APB=45º,PC=BC= ,求PA的长.
【例3】如图,在正△ABC中,点D为△ABC外一点,且满足∠BDC=120º,探究DB,DA,DC三者之间满足什么样的数量关系?并说明你的理由.
解：DA=DB+DC.理由如下：将△ABD绕点A逆时针旋转60º至△ACH,则有△ABD≌△ACH,∠ABD=∠ACH,BD=CH.∵△ADH为等边三角形,∴DA=DH∵∠BDC=120º,∠BAC=60º,∴∠ABD+∠ACD=180º,∴∠ACH+∠ACD=180º,∴D,C,H三点共线(必须证三点共线,否则扣分)∵DH=DC+CH,∴DA=DC+DB.
【例3】如图,已知正方形ABCD,点E为正方形ABCD外一点,AE= ,DE=1,求线段CE的最大值？
解：将△EDC绕点D顺时针旋转90º至△HDA,则有： △EDC≌△HDA,CE=AH,DE=DH,∠EDH=90º, ∵在等腰直角△EDH中, ∴EH=√2DE=√2。 ∴AH≤AE+EH=2√2+√2=3√2, 又∵CE=AH, ∴CE≤3√2.
两个定点----两点之间线段最短
1.如图,在四边形ABCD中,AB=4,BC=3,△ACD为等边三角形,则BD的最大值为____.
2.如图,△ABC是边长为4的等边三角形,AD为BC边上的高线,点E为线段AD上一动点,连接CE,将CE绕点C逆时针旋转60º得到线段CF,连接DF.DF的最小值是____.
一个定点----垂线段最短
1.如图,在等腰Rt△ACB中,∠ACB=90º,D为△ACB外一点,且满足∠ADC=45º,AD=3,CD=4,求BD的长？
解：将△DCB绕点C顺时针旋转90º至△HCA,则有△DCB≌△HCA ，∴DC=HC,∠DCH=90º,∠HDC=45º,CH=DC=4,∵∠ADC=45º∴∠HDA=∠ADC+∠CDH=90º在Rt△ADH中AD=3,DH=4√2 ,∴AH=√(AD2+DH2)=√(9+32)=√41∴ BD=AH=√41.
2.已知如图,在四边形ABCD中,∠ADC=60º,∠ABC=30º,且AD=AC。求证BA2+BC2=BD2 。
解：将△ADB绕点A逆时针旋转60º至△ACH, 可得△ABH为等边三角形, ∵∠ABC=30º,∴∠CBH=∠ABC+∠HBA=90º,又∵△ADB≌△ACH,∴BD=HC, ∵在直角△CBH中,CH2=BC2+BH2,又∵在等边△ABH中,AB=BH ∴ BD2=BC2+AB2。
(1)将△APD绕点D逆时针旋转90º 得△CQD,再连接PQ,
(2)作CH⊥DQ于点H，
求得∠APD=∠CQD=45º+90º=135°
4.已知△AOB和△COD均为等腰直角三角,∠AOB=∠COD=90º,连接AD,BC,点H为BC的中点,连接OH.(1)如图1所示,求证：OH=0.5AD且OH⊥AD
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论．
5.已知∠MAN=135º,正方形ABCD绕点A旋转。(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M,N,连接MN．①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是________;②如图2,若BM≠DN,请判断①中的数量关系是否仍成立？若成立,请给予证明;若不成立,请说明理由；