专题04 求不规则图形的面积中圆的应用-2021-2022学年九年级数学上册难点突破（人教版）

这是一份专题04 求不规则图形的面积中圆的应用-2021-2022学年九年级数学上册难点突破（人教版），文件包含专题04求不规则图形的面积中圆的应用解析版docx、专题04求不规则图形的面积中圆的应用原卷版docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
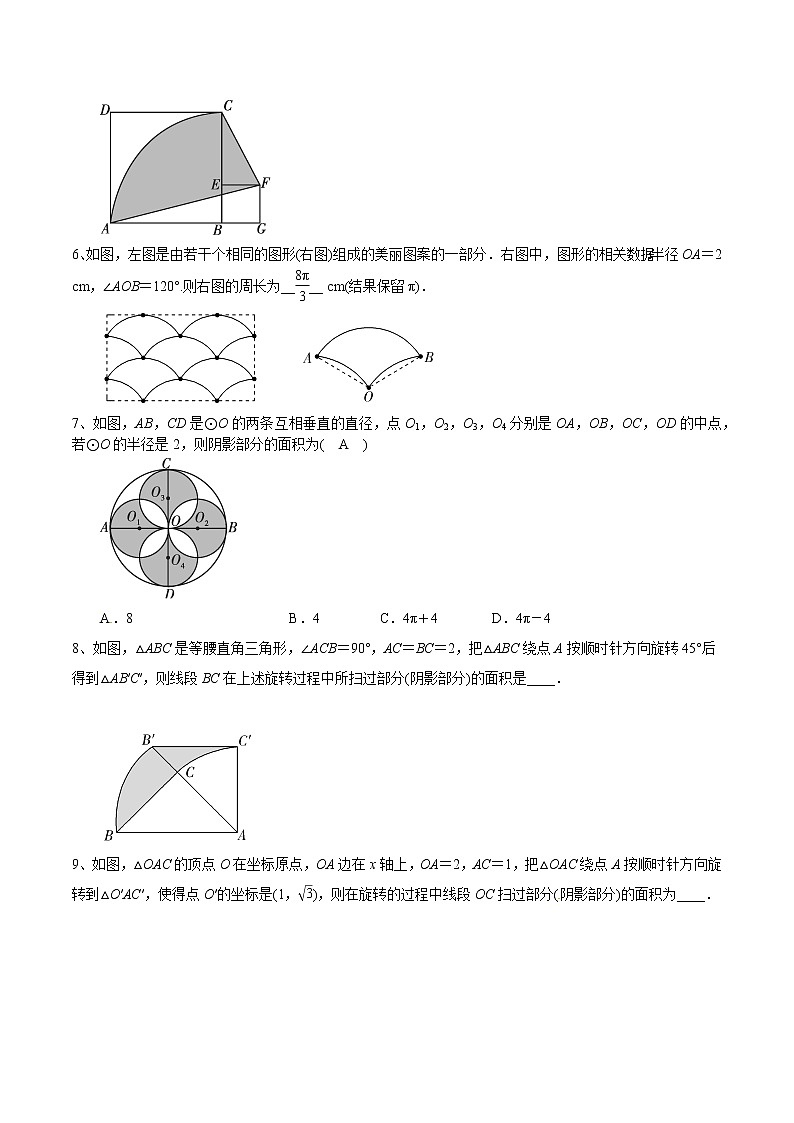
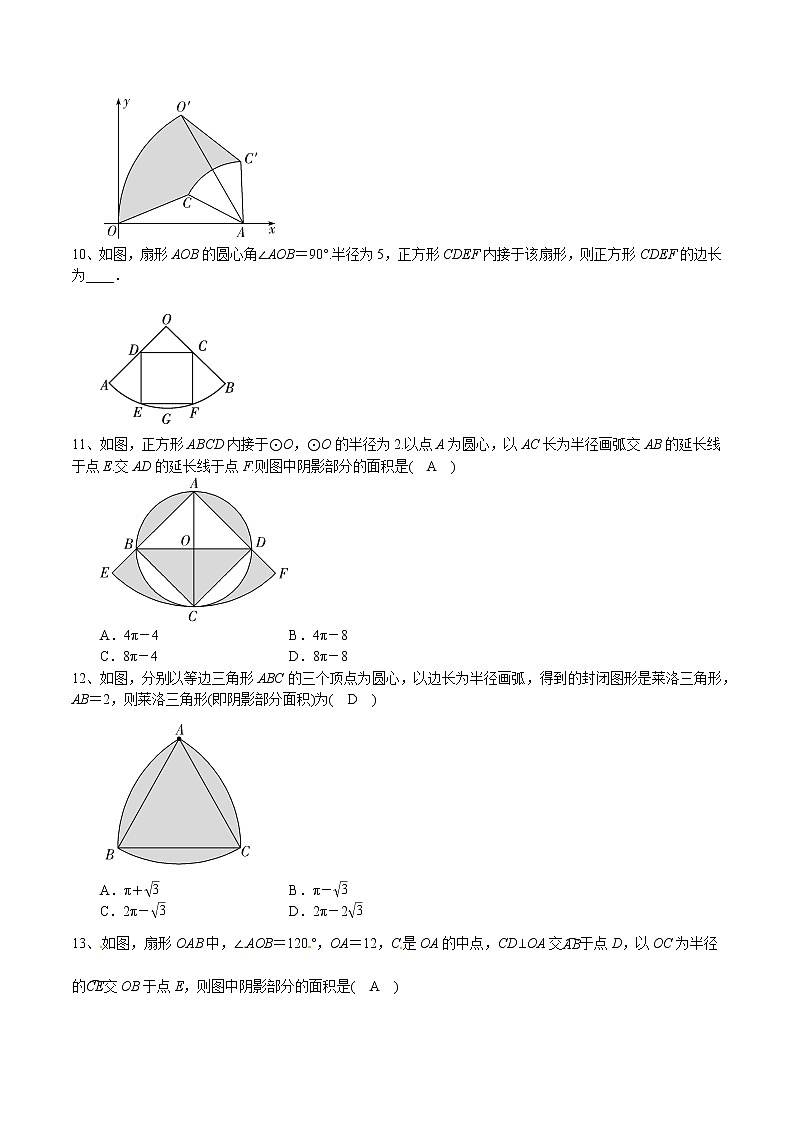
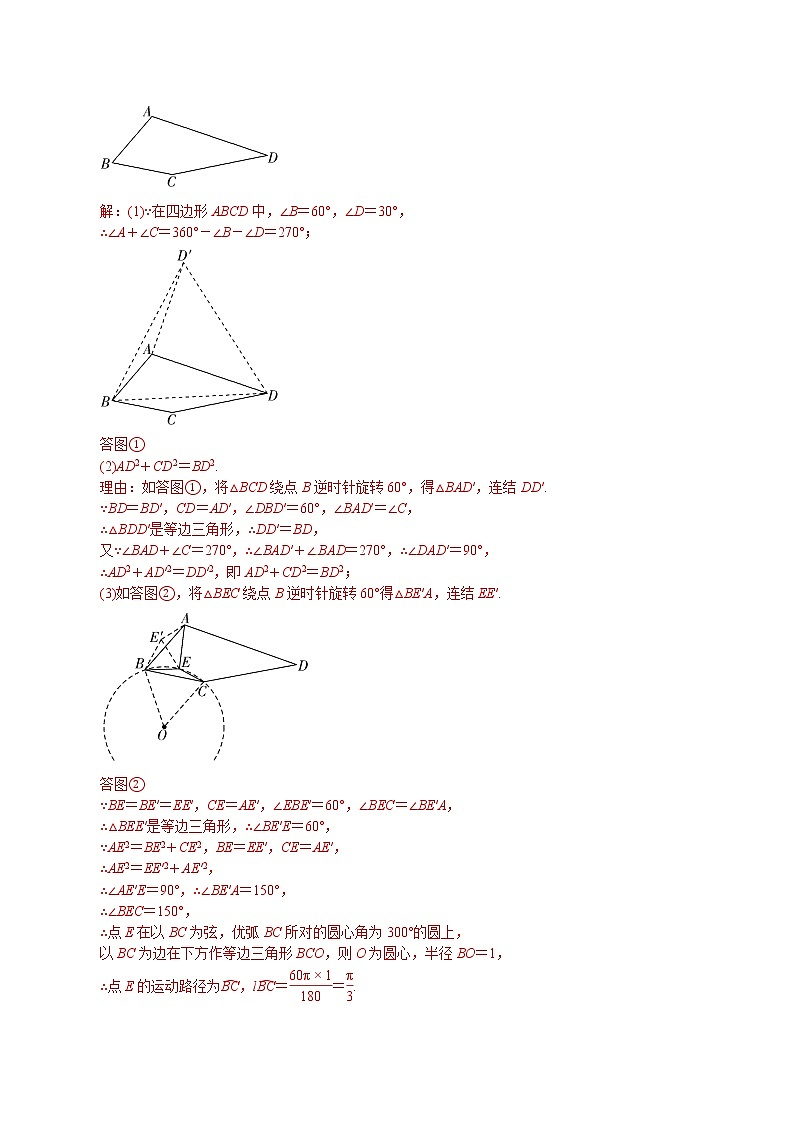
专题04 求不规则图形的面积中圆的应用求不规则图形的面积求不规则图形的面积常利用对称、全等及平行线进行等面积的图形转换，转化为容易解决的规则图形，然后求出各图形的面积，通过面积的和差求出结果．1、如图，四边形ABCD是菱形，∠A＝60°，AB＝2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是(　B　)A.－   B.－C．π－  D．π－【解析】 如答图，连结BD，∵四边形ABCD是菱形，∠A＝60°，答图∴∠ADC＝120°，∴∠1＝∠2＝60°，∴△DAB是等边三角形，∵AB＝2，∴△ABD的高为，∵扇形BEF的半径为2，圆心角为60°，∴∠4＋∠5＝60°，∵∠3＋∠5＝60°，∴∠3＝∠4，△ABG≌△DBH(ASA)，∴四边形GBHD的面积等于△ABD的面积，∴图中阴影部分的面积是S扇形EBF－S△ABD＝－×2×＝－.3、如图，AB为⊙O的直径，且AB＝4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连结OM，PM.(1)求∠OMP的度数；(2)当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．[来源:学#科#网Z#X#X#K][来源:Zxxk.Com]解：(1)∵△OPE的内心为M，∴∠MOP＝∠EOP，∠MPO＝∠EPO，∵PE⊥OC，∴∠PEO＝90°，∠EOP＋∠EPO＝90°，∴∠MOP＋∠MPO＝(∠EOP＋∠EPO)＝×90°＝45°，∴∠OMP＝180°－45°＝135°；(2)如答图，连结CM，答图∵OM＝OM，∠COM＝∠POM，CO＝PO，∴△COM≌△POM，∴∠CMO＝∠PMO＝135°，点M的运动轨迹是两个，设的圆心为O1，∵∠CMO＝135°，∴弦CO所对的劣弧的圆周角为45°，∴∠CO1O＝90°，在Rt△CO1O中，CO1＝sin  45°×OC＝×2＝，当点P在半圆上从点B运动到点C时，内心M所经过的路径为⊙O1的劣弧OC，∴l＝＝π，同理，当点P在半圆上从点C运动到点A时，内心M所经过的路径为⊙O2对应的劣弧OC与⊙O1的劣弧OC长度相等，∴当点P在半圆上从点B运动到点A时，内心M所经过的路径长为π＋  π＝π.4、如图，在四边形ABCD中，∠B＝60°，∠D＝30°，AB＝BC.(1)求∠A＋∠C的度数；(2)连结BD，探究AD，BD，CD三者之间的数量关系，并说明理由；(3)若AB＝1，点E在四边形ABCD内部运动，且满足AE2＝BE2＋CE2，求点E运动路径的长度．解：(1)∵在四边形ABCD中，∠B＝60°，∠D＝30°，∴∠A＋∠C＝360°－∠B－∠D＝270°；答图①[来源:Zxxk.Com](2)AD2＋CD2＝BD2.理由：如答图①，将△BCD绕点B逆时针旋转60°，得△BAD′，连结DD′.∵BD＝BD′，CD＝AD′，∠DBD′＝60°，∠BAD′＝∠C，∴△BDD′是等边三角形，∴DD′＝BD，又∵∠BAD＋∠C＝270°，∴∠BAD′＋∠BAD＝270°，∴∠DAD′＝90°，∴AD2＋AD′2＝DD′2，即AD2＋CD2＝BD2；(3)如答图②，将△BEC绕点B逆时针旋转60°得△BE′A，连结EE′.答图②∵BE＝BE′＝EE′，CE＝AE′，∠EBE′＝60°，∠BEC＝∠BE′A，∴△BEE′是等边三角形，∴∠BE′E＝60°，∵AE2＝BE2＋CE2，BE＝EE′，CE＝AE′，∴AE2＝EE′2＋AE′2，∴∠AE′E＝90°，∴∠BE′A＝150°，∴∠BEC＝150°，∴点E在以BC为弦，优弧BC所对的圆心角为300°的圆上，以BC为边在下方作等边三角形BCO，则O为圆心，半径BO＝1，∴点E的运动路径为，l＝＝.  5、如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画，连结AF，CF，则图中阴影部分面积为__4π__．6、如图，左图是由若干个相同的图形(右图)组成的美丽图案的一部分．右图中，图形的相关数据：半径OA＝2 cm，∠AOB＝120°.则右图的周长为____ cm(结果保留π)．【解析】 ∵半径OA＝2 cm，∠AOB＝120°∴l＝＝，l＋l＝，∴右图的周长＝＋＝.7、如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA，OB，OC，OD的中点，若⊙O的半径是2，则阴影部分的面积为(　A　)A．8  B．4    C．4π＋4   D．4π－4【思路生成】连结相邻小圆的交点，构造正方形，求出正方形中空白部分的面积，进而得出阴影面积．答图【解析】 如答图所示，可得正方形EFMN，边长为2，正方形中阴影部分的面积为S1＝2(22－π×12)＝8－2π，∵⊙O的半径为2，∴O1，O2，O3，O4的半径为1，∴小圆的面积为π×12＝π，∴S阴影＝2S小圆＋S1＝2π＋(8－2π)＝8.[来源:学,科,网Z,X,X,K]8、如图，△ABC是等腰直角三角形，∠ACB＝90°，AC＝BC＝2，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__π__．[来源:Z+xx+k.Com] 【解析】 S阴影＝S扇形ABB′＋S△AC′B′－S扇形ACC′－S△ABC＝S扇形ABB′－S扇形ACC′＝×π×(2)2－×π×22＝π.9、如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA＝2，AC＝1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是(1，)，则在旋转的过程中线段OC扫过部分(阴影部分)的面积为____．【解析】 如答图，过点O′作O′H⊥x轴于点H，∵点O′的坐标是(1，)，∴OH＝1，O′H＝，又∵AO＝AO′＝2，∴∠HAO′＝60°，即旋转∠OAO′＝∠CAC′＝60°，根据旋转的性质可知，△OAC≌△O′AC′，∴△OAC的面积与△O′AC′的面积相等，答图∴S阴影＝S扇形OAO′＋S△O′C′A－S△OCA－S扇形CAC′＝S扇形OAO′－S扇形CAC′＝－＝.10、如图，扇形AOB的圆心角∠AOB＝90°.半径为5，正方形CDEF内接于该扇形，则正方形CDEF的边长为____． 【解析】 如答图，过点O作OH⊥EF交EF于点H，交DC于点K，连结OF.∵OH过圆心，∴EH＝FH.答图∵四边形CDEF是正方形，∴OH⊥DC，DK＝CK，∴△OCK是等腰直角三角形，OK＝KC.设CF＝x，则KH＝x，HF＝OK＝CK＝，在Rt△OHF中，OH2＋HF2＝OF2，即＋＝52，解得x＝，即CF的长为.11、如图，正方形ABCD内接于⊙O，⊙O的半径为2.以点A为圆心，以AC长为半径画弧交AB的延长线于点E.交AD的延长线于点F.则图中阴影部分的面积是(　A　)A．4π－4  B．4π－8C．8π－4  D．8π－8【解析】 根据对称，阴影部分的面积可以转化为答图，答图则S阴影＝S扇形－S△ABD＝－×4×2＝4π－4.12、如图，分别以等边三角形ABC的三个顶点为圆心，以边长为半径画弧，得到的封闭图形是莱洛三角形，AB＝2，则莱洛三角形(即阴影部分面积)为(　D　)A．π＋  B．π－C．2π－  D．2π－2【解析】 莱洛三角形的面积实际上是由三块相同的扇形叠加而成，其面积等于三块扇形的面积相加减去两个等边三角形的面积，即S阴影＝3×S扇形－2S△ABC.答图由题意得S扇形＝π×22×＝π，S△ABC＝×22＝，∴S阴影＝3S扇形－2S△ABC＝3×π－2×＝2π－2.13、如图，扇形OAB中，∠AOB＝120°，OA＝12，C是OA的中点，CD⊥OA交于点D，以OC为半径的交OB于点E，则图中阴影部分的面积是(　A　)A．12π＋18  B．12π＋36C．6π＋18  D．6π＋36【解析】 如答图，连结OD，AD，答图∵点C为OA的中点，∴OC＝OA＝OD，∵CD⊥OA，∴∠CDO＝30°，∠DOC＝60°，∴△ADO为等边三角形，OD＝OA＝12，OC＝CA＝6，∴CD＝＝6，∴S扇形AOD＝＝24π，∴S阴影＝S扇形AOB－S扇形COE－(S扇形AOD－S△COD)＝－－(24π－×6×6)＝12π＋18.14、如图，矩形ABCD中，BC＝4，CD＝2，以AD为直径的半圆O与BC相切于点E，连结BD，则阴影部分的面积为__π__．(结果保留π)【解析】 连结OE，易证四边形ABEO为正方形，则扇形OED的圆心角为90°，半径为2，因此可求扇形OED的面积，阴影面积看成正方形ABEO＋扇形OED－三角形ABD，正方形ABEO和三角形ABD面积均可求，即可求得阴影部分．15、如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′，其中点B的运动路径为弧BB′，则图中阴影部分的面积为__π－__．【解析】 如答图，连结B′D，BD，B′B，答图∵∠ACB＝90°，AC＝BC＝2，将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′，∴C′D＝CD＝1，B′C′＝BC＝2，∠CDC′＝∠C′＝∠B′DB＝90°，∴B′D＝BD＝＝，∴CD∥B′C′，B′C＝A′C＝A′B＝，∴S阴影＝S扇形BDB′－S△BDB′＋S△B′BC＝－××＋××＝π－.16、如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，4)，B(1，1)，C(3，1)．(1)画△ABC关于x轴对称的△A1B1C1；(2)画△ABC绕点O逆时针旋转90°后的△A2B2C2；(3)在(2)的条件下，求线段BC扫过的面积(结果保留π)．解：(1)画出△A1B1C1如答图所示；答图(2)画出△A2B2C2如答图所示；(3)∵OC＝＝，OB＝＝，∴S＝S扇形OCC2－S扇形OBB2＝π(OC2－OB2)＝2π.17、如图，是某公园的一角，∠AOB＝90°，的半径OA长是6 m，点C是OA的中点，点D在上，CD∥OB，则图中草坪区(阴影部分)的面积是(　A　)A.m2B.m2C.m2D.m218、如图，在正方形ABCD中，AD＝2，E是AB的中点，将△BEC绕点B逆时针旋转90°后，点E落在CB的延长线上点F处，点C落在点A处．再将线段AF绕点F顺时针旋转90°得线段FG，连结EF，CG.(1)求证：EF∥CG；(2)求点C，点A在旋转过程中形成的，与线段CG所围成的阴影部分的面积．解：(1)证明：∵四边形ABCD是正方形，∴AB＝BC＝AD＝2，∠ABC＝90°.∵△BEC绕点B逆时针旋转90°得△BFA，∴△ABF≌△CBE，∴∠FAB＝∠ECB，∠ABF＝∠CBE＝90°，AF＝EC，∴∠AFB＋∠FAB＝90°.∵线段AF绕点F顺时针旋转90°得线段FG，∴∠AFB＋∠CFG＝∠AFG＝90°，AF＝FG，∴∠CFG＝∠FAB＝∠ECB，∴EC∥FG.∵AF＝EC，AF＝FG，∴EC＝FG，∴四边形EFGC是平行四边形，∴EF∥CG；(2)∵△ABF≌△CBE，∴FB＝BE＝AB＝1，∴AF＝＝.在△FEC和△CGF中，∵EC＝FG，∠ECF＝∠GFC，FC＝CF，∴△FEC≌△CGF，∴S△FEC＝S△CGF，∴S阴影＝S扇形ABC＋S△ABF＋S△FGC－S扇形AFG＝＋×2×1＋×(1＋2)×1－＝－.