2020-2021学年26.1.2 反比例函数的图象和性质教学课件ppt

这是一份2020-2021学年26.1.2 反比例函数的图象和性质教学课件ppt
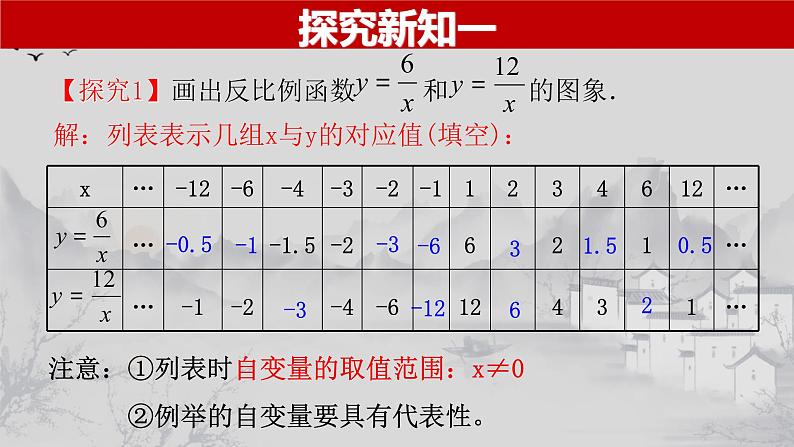
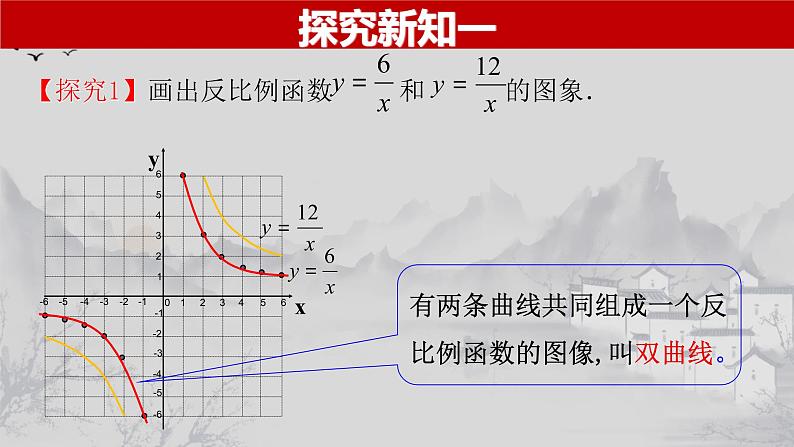
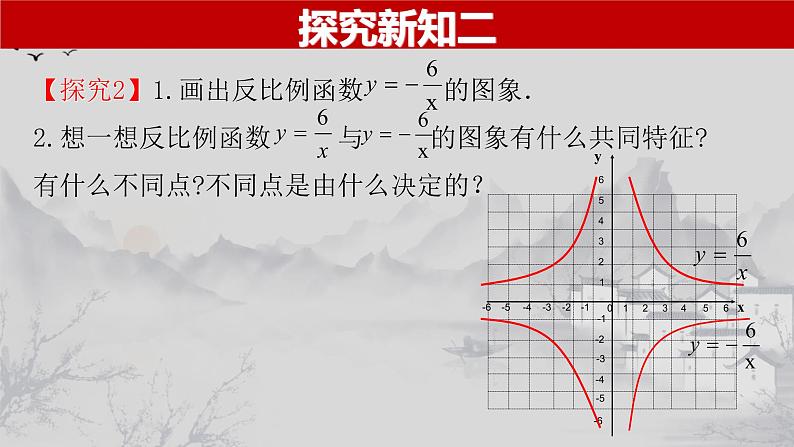
人教版九年级数学(下)教学课件第二十六章 反比例函数§26.1.2 反比例函数的图象和性质(第1课时)导入新课你还记得作函数图象的方法和一般步骤吗?函数图象画法列表描点连线描点法当k＞0时,反比例函数的图象及性质当k＜0时,反比例函数的图象及性质探究新知一 解：列表表示几组x与y的对应值(填空)：-0.5-126-12-30.51.53-6-3注意：①列表时自变量的取值范围：x≠0 ②例举的自变量要具有代表性。探究新知一123456-1-3-2-4-5-61234-1-2-3-40-6-556xy有两条曲线共同组成一个反比例函数的图像,叫双曲线。知识归纳一(1)由两条曲线组成,且分别位于第一、三象限它们与 x 轴、y轴都不相交；(2)在每个象限内,y随x的增大而减小.当k＞0时,反比例函数的图象及性质当k＜0时,反比例函数的图象及性质探究新知二123456-1-3-2-4-5-61234-1-2-3-40-6-556yx探究新知二知识归纳二(1)由两条曲线组成，且分别位于第二、四象限它们与x轴、y轴都不相交；(2)在每个象限内，y随x的增大而增大.知识归纳二(1)当k＞0时,双曲线的两支分别位于第一、三象限,在每一象限内,y随x的增大而减小；(2)当k＜0时,双曲线的两支分别位于第二、四象限,在每一象限内,y随x的增大而增大.k的正负决定反比例函数所在的象限和增减性典型例题二【例1】已知反比例函数 ,在每一象限内,y随x的增大而增大,求a的值.解：由题意得a2+a-7=-1,且a-1＜0． 解得 a=-3.典型例题二C当堂训练二B2.反比例函数 的图象大致是( )C3.点(2,y1)和(3,y2)在函数 上,则y1 y2(填“＞”“＜”或“＝”).＞解：由题意得 m2-10=-1,且3m-8＞0． 解得 m=3.函数图象的两支分支分别位于第一、三象限函数图象的两支分支分别位于第二、四象限在每一支曲线上,y都随x的增大而减小在每一支曲线上,y都随x的增大而增大双曲线向四边无限延伸,与坐标轴没有交点.双曲线既是轴对称图形(对称轴:y=±x),又是中心对称图形(对称中心:O).|k|越大,双曲线离坐标轴越远.补 充 练 习C利用增减性求待定系数的取值范围m＞2利用增减性求待定系数的取值范围AD4.已知反比例函数y=mxm²－5,它的两个分支分别在第一、第三象限,求m的值.5.已知反比例函数y=(a-1)xa²+a－7,当x＞0,y随x的增大而增大, 求a的值.a=-3利用增减性求待定系数的取值范围m=2.【例3】反比例函数 的图象上有两点P1(x1,y1),P2(x2,y2),若x1＜0＜x2,则下列结论正确的是( ) A.y1＜y2＜0 B.y1＜0＜y2 C.y1＞y2＞0 D.y1＞0＞y2 D利用反比例函数图象比较函数值的大小1.已知反比例函数 的图象过点(-2,-3),函数图象上有两点A( ),B(5,y2),则y1与y2的大小关系为( )A.y1＞y2 B.y1＝y2 C.y1＜y2 D.无法确定2.点(2,y1)和(3,y2)在函数 上,则y1 _____y2(填“＞”“＜”或“＝”).3.已知反比例函数 的图象过点(-2,-3),图象上有两点A(x1,y1),B(x2,y2),且x1＞x2＞0,则y1-y2 0.C＜利用反比例函数图象比较函数值的大小＜1.下列关于反比例函数 的图象的三个结论： (1)经过点(-1,12) 和点(10,-1.2)； (2)在每一个象限内,y随x的增大而减小； (3)双曲线位于二、四象限. 其中正确的是 (填序号).(1)(3)培 优 训 练1.如图所示,直线y=kx(k＜0)与双曲线 交于(x1,y1),B(x2,y2)两点,则3x1y2-8x2y1的值为( ) A.-5 B.-10 C.5 D.10B利用反比例函数图象的对称性求值 解：由题意知,在图象的每一支上,y 随 x 的增大而减小. ① 当这两点在图象的同一支上时， ∵y1＜y2，∴a－1＞a+1，无解； ②当这两点分别位于图象的两支上时， ∵y1＜y2，∴必有 y1＜0＜y2. ∴a－1＜0，a+1＞0，解得：－1＜a＜1. 故a的取值范围为：－1＜a＜1．