



初中数学人教版九年级下册26.1.1 反比例函数教学课件ppt
展开反比例函数解析式中 k 的几何意义
利用k的几何意义求图形的面积
利用图形的面积求解析式中k的值
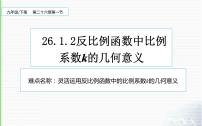
过反比例函数 图象上任一点 P作x轴、y轴的垂线PM、PN,求:(1)四边形PMON的面积. (2)△PMO,△PNO的面积.
考查点1:利用k的几何意义求图形的面积(高频考点)
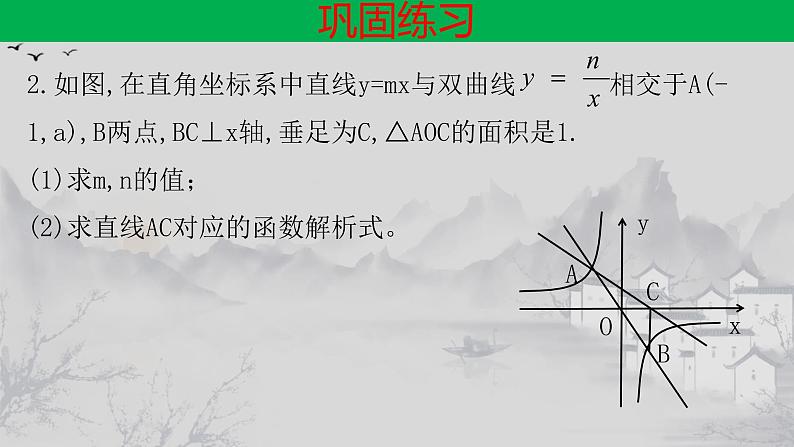
2.如图,在直角坐标系中直线y=mx与双曲线 相交于A(-1,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是1.(1)求m,n的值;(2)求直线AC对应的函数解析式。
考查点2:利用图形的面积求解析式中k的值
【例2】如图,矩形AOBC的面积为4,反比例函数 的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( ) A. B. C. D.
考查点3:利用面积确定解析式时易忽视图象所在的象限
【例3】如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为________.
提高点1:利用反比例函数图象上点的坐标特征解决问题
【例4】如图,P1、P2是反比例函数 在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.(1)求反比例函数的解析式.(2)①求P2的坐标.②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数 的函数值.
提高点2:利用比例系数k的几何意义探究点的坐标的变化规律
【例5】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线 (x>0于)点C1,C2,…,Cn-1。若C15B15=16C15A15,则n的值为____,(n为正整数)
(1)B(3,3),k=9(2)P(6,1.5)或(1.5,6)(3)S=9-27/m或S=9-3m
4.已知反比例函数 (m为常数)的图象在一、三象限.(1)求m的取值范围;(2)如图,若该反比例函数的图象经过□ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0).①求出函数解析式;②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为_______________________;若以D、O、P为顶点的三角形是等腰三角形,则满足条件的点P的个数为___个.
(-2,-3),(3,2),(-3,-2)
提高点1:利用数形结合思想解决反比例函数与几何的综合问题(相似)
【例4】如图,若双曲线 与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为______.
1.如图,已知双曲线 与直线y=-x+6相交于点A,B两点,过点A作x轴的垂线,与过点B作y轴的垂线相交于点C,若△ABC的面积为8,则k的值为___.
3.如图,AC⊥x轴于点A,点B在y的正半轴上,∠ABC=60º,AB=4,BC= ,点D为AC与反比例函数 的图形的交点,若直线BD将△ABC的面积分成1:2的两部分,则k的值为_________.
【思路点拨】1.过点C作CD⊥AB于点D,求△ABC的面积;2.过点C作CH⊥AB于点H,求矩形ACHO的面积;3.利用矩形ACHO的面积的1/3或2/3求出k的值。
2.若在反比例函数 中也用同样的方法分别取P、Q两点,填写表格:
由前面的探究过程,可以猜想:
我们就 k < 0 的情况给出证明:
设点 P 的坐标为 (a,b)
∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;
若点 P 在第二象限,则 a<0,b>0,
若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP=PB·PA=a· (-b)=-ab=-k.
综上,S矩形 AOBP=|k|.
自己尝试证明 k > 0的情况.
点 Q 是其图象上的任意一 点,作 QA 垂直于 y 轴,作 QB 垂直于x 轴,矩形AOBQ 的面积与 k 的关系是 S矩形AOBQ= . 推理:△QAO与△QBO的 面积和 k 的关系是 S△QAO=S△QBO= .
反比例函数的面积不变性
A. SA >SB>SC B. SA
解:设点 A 的坐标为(xA,yA),∵点 A 在反比例函数 的图象上,∴ xA·yA=k,∴ S△AOC= ·k=2,∴ k=4,∴反比例函数的表达式为
1. 如图,过反比例函数 图象上的一点 P,作 PA⊥x 轴于A. 若△POA 的面积为 6,则 k = .
提示:当反比例函数图象在第二、四象限时,注意 k<0.
2. 若点 P 是反比例函数图象上的一点,过点 P 分别向 x 轴、y 轴作垂线,垂足分别为点 M,N,若四边形 PMON 的面积为 3,则这个反比例函数的关系式是 .
例4 如图,P,C是函数 (x>0) 图像上的任意两点,PA,CD 垂直于 x 轴. 设 △POA 的面积为 S1,则 S1 = ;梯形CEAD 的面积为 S2,则 S1 与 S2 的大小关系是 S1 S2;△POE 的面积 S3 和 S2 的大小关系是S2 S3.
如图,直线与双曲线交于 A,B 两点,P 是AB 上的点,△ AOC 的面积 S1、△ BOD 的面积 S2、 △ POE 的面积 S3 的大小关系为 .
S1 = S2 < S3
解析:由反比例函数面积的不变性易知 S1 = S2. PE 与双曲线的一支交于点 F,连接 OF,易知,S△OFE = S1 = S2,而 S3>S△OFE,所以 S1,S2,S3的大小关系为S1 = S2 < S3
方法总结:解决反比例函数有关的面积问题,可以把原图形通过切割、平移等变换,转化为较容易求面积的图形.
如图,函数 y=-x 与函数 的图象相交于 A,B 两点,过点 A,B 分别作 y 轴的垂线,垂足分别为C,D,则四边形ACBD的面积为 ( ) A. 2 B. 4 C. 6 D. 8
沪科版九年级上册第21章 二次函数与反比例函数21.5 反比例函数教学ppt课件: 这是一份沪科版九年级上册第21章 二次函数与反比例函数21.5 反比例函数教学ppt课件,共13页。
初中人教版26.1.1 反比例函数教学ppt课件: 这是一份初中人教版26.1.1 反比例函数教学ppt课件,共14页。
数学九年级下册26.1.2 反比例函数的图象和性质教学ppt课件: 这是一份数学九年级下册26.1.2 反比例函数的图象和性质教学ppt课件,共25页。PPT课件主要包含了强化训练,拓展提升,-8或-4,拓展提高,当堂训练等内容,欢迎下载使用。