初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教学ppt课件

这是一份初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用教学ppt课件，共14页。PPT课件主要包含了导入新课1分钟，探究新知，典型例题，当堂训练，课堂小结，补充练习，基础练习等内容，欢迎下载使用。
【问题1】平时观察物体时，我们的视线相对于水平线来说可有几种情况？
三种：重叠、向上和向下。
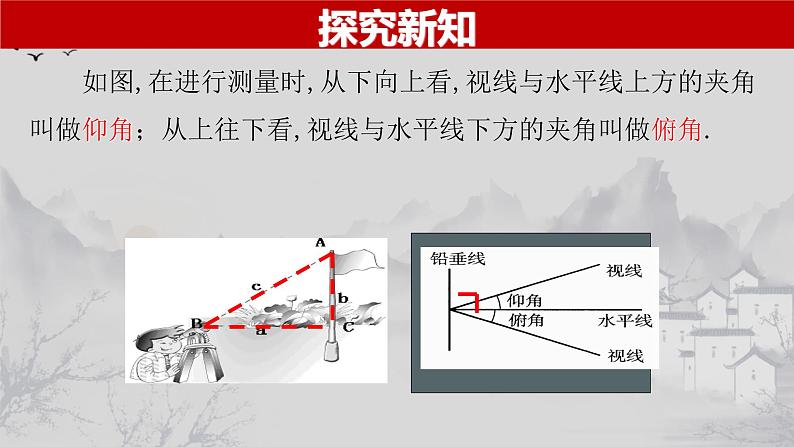
从下向上看，视线与水平线的夹角叫做仰角；
从上向下看，视线与水平线的夹角叫做俯角。
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角；从上往下看,视线与水平线下方的夹角叫做俯角.
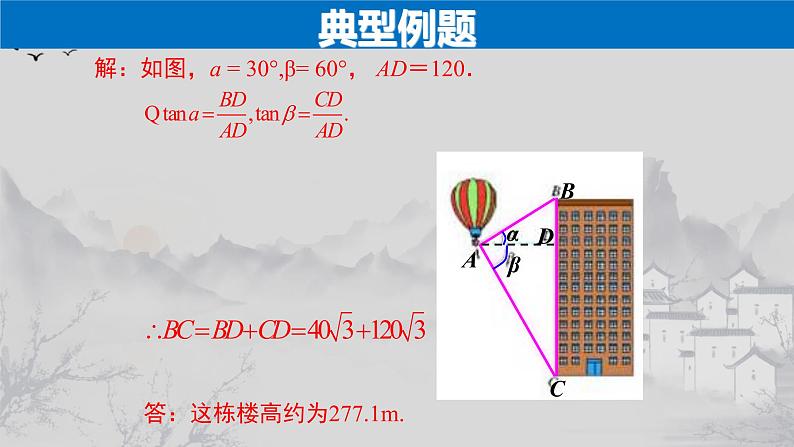
【例1】热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30º,看这栋高楼底部的俯角为60º,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析：我们知道，在视线与水平线所成的角中视线在水平线上方的是仰角，视线在水平线下方的是俯角，因此，在图中，a=30°，β=60°.
Rt△ABD中，a =30°，AD＝120，所以利用解直角三角形的知识求出BD的长度；类似地可以求出CD的长度，进而求出BC的长度，即求出这栋楼的高度.
解：如图，a = 30°,β= 60°， AD＝120．
答：这栋楼高约为277.1m.
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54º,观察底部B的仰角为45º,求旗杆的高度(精确到0.1m).
解：在等腰Rt△BCD中，∠ACD=90°，
∴AB=AC－BC=55.2－40=15.2 (m).
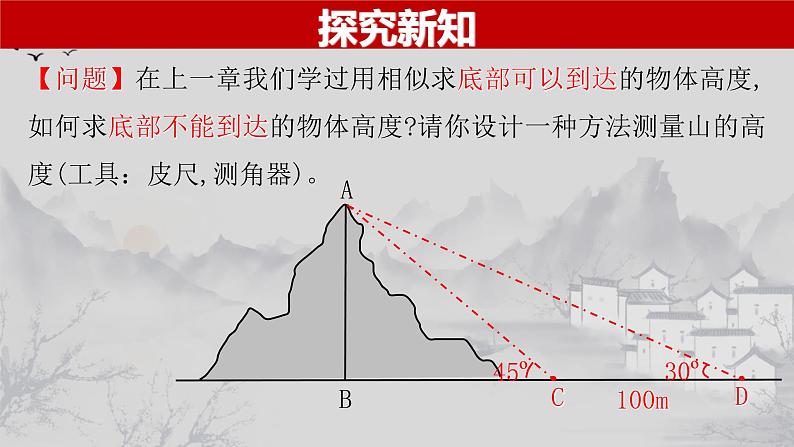
【问题】在上一章我们学过用相似求底部可以到达的物体高度,如何求底部不能到达的物体高度?请你设计一种方法测量山的高度(工具：皮尺,测角器)。
【例3】如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30º,再往塔的方向前进50m至C处.测得仰角为60º,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?
解：如图，由题意可知,∠AD´B´=30º,∠AC´B´=60º,D´C´=50m.∴∠D´AB´=60º,∠C´AB´=30º,D´C´=50m,设AB´=xm.
1.如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37º和45º,求飞机的高度.(结果取整数.参考数据：sin37º≈0.8,cs37º≈0.6,tan3º≈0.75)
在Rt△POB中，∠PBO=45º,
在Rt△POA中，∠PAB=37°，
解：作PO⊥AB交AB的延长线于O.
故飞机的高度为1200米.
2.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角54º,观察底部B的仰角为45º,求旗杆的高度(精确到0.1m)(sin54º≈0.809；cs54º≈0.588；tan54º≈1.38)
利用仰俯角解直角三角形
运用解直角三角形解决仰角、俯角问题
仰角、俯角问题的常见基本模型：
1.如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请求出大树的高.