专训三十九：二次函数与几何综合：平行四边形存在性判定-2021-2022学年九年级数学上册计算力提升训练（人教版）

这是一份专训三十九：二次函数与几何综合：平行四边形存在性判定-2021-2022学年九年级数学上册计算力提升训练（人教版），文件包含专训三十九二次函数与几何综合平行四边形存在性判定解析版docx、专训三十九二次函数与几何综合平行四边形存在性判定原卷版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
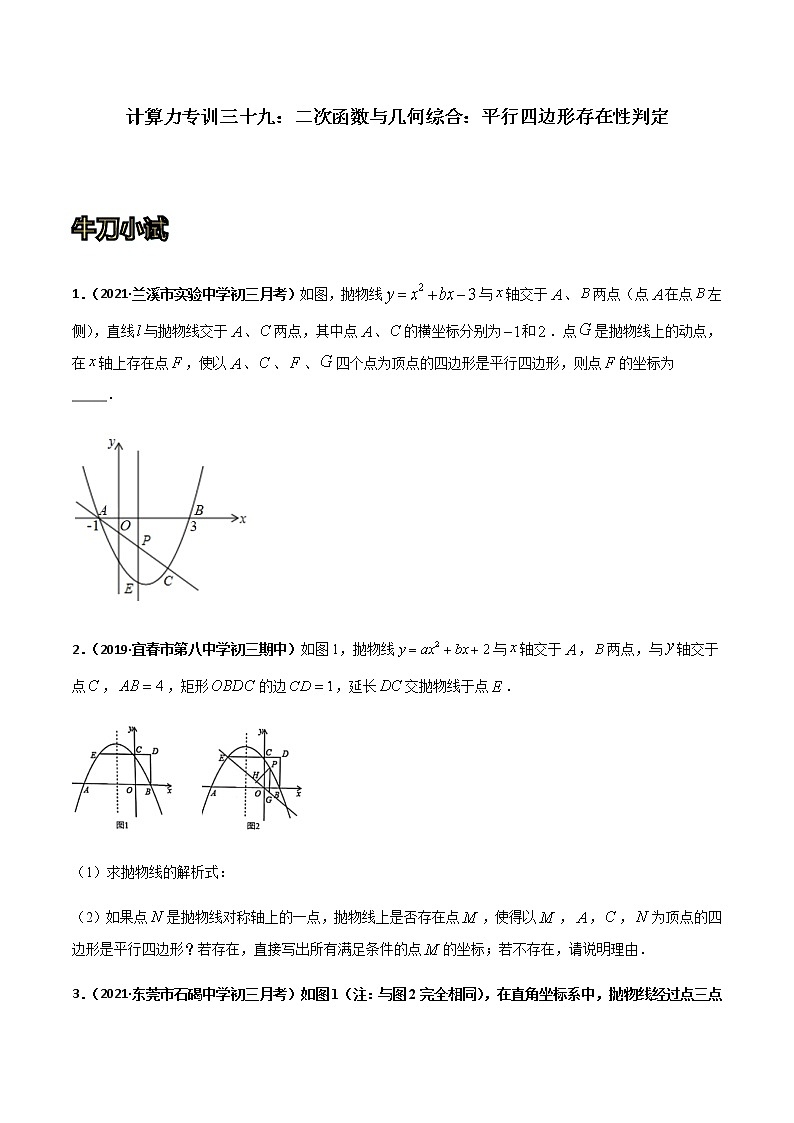
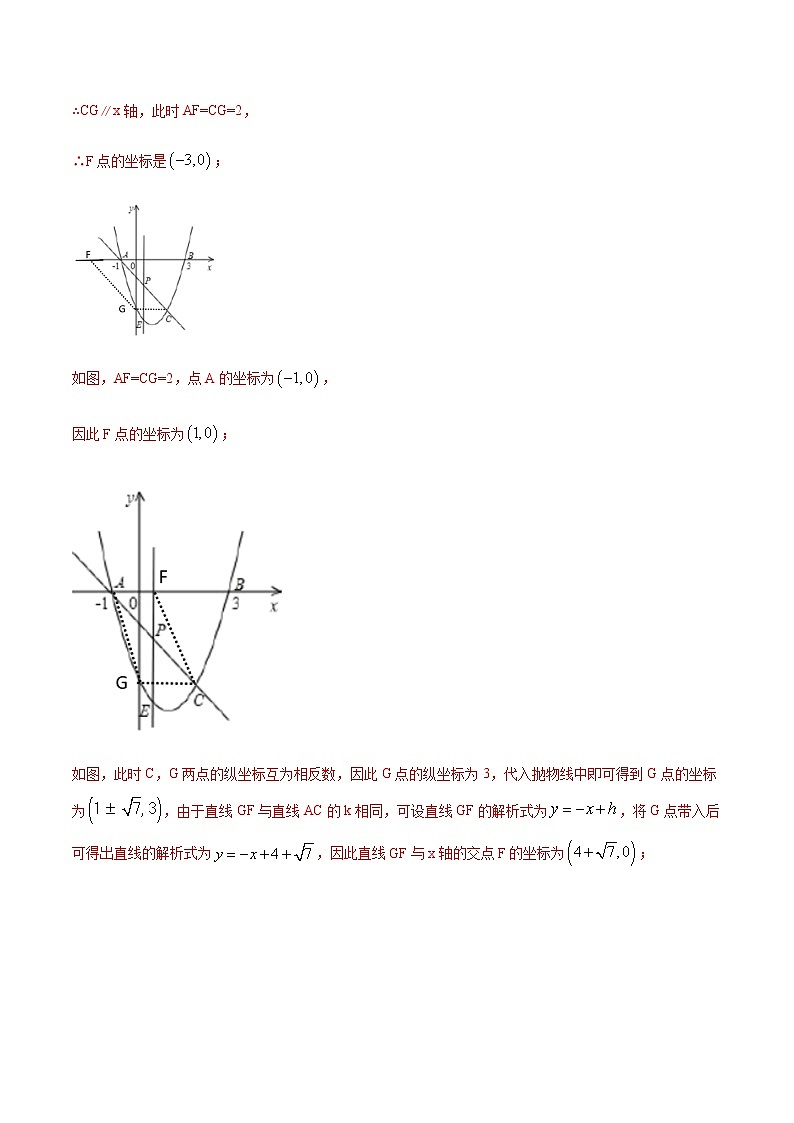
计算力专训三十九：二次函数与几何综合：平行四边形存在性判定 牛刀小试1．（2021·兰溪市实验中学初三月考）如图，抛物线与轴交于、两点（点在点左侧），直线与抛物线交于、两点，其中点、的横坐标分别为和．点是抛物线上的动点，在轴上存在点，使以、、、四个点为顶点的四边形是平行四边形，则点的坐标为_____．2．（2019·宜春市第八中学初三期中）如图1，抛物线与轴交于，两点，与轴交于点，，矩形的边，延长交抛物线于点．     （1）求抛物线的解析式：（2）如果点是抛物线对称轴上的一点，抛物线上是否存在点，使得以，，，为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由．3．（2021·东莞市石碣中学初三月考）如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点,,．（1）求抛物线的解析式和对称轴；（2）在第四象限的抛物线上是否存在点，使四边形是以为对角线且面积为的平行四边形？若存在，请求出点坐标，若不存在请说明理由.（请在图2中探索）4．（2021·齐齐哈尔市第二十八中学初三月考）在平面直角坐标系中，二次函数 y＝ax2＋bx＋2 的图象与 x 轴交于 A（﹣3，0），B（1，0）两点，与 y 轴交于点C． （1）求这个二次函数的关系解析式 ，x 满足什么值时 y﹤0 ? （2）点 M 为抛物线上一动点，在 x 轴上是否存在点 Q，使以 A、C、M、Q 为顶点的四边形是平行四边形？若存在，直接写出点 Q 的坐标；若不存在，说明理由．5．（2021·合肥工业大学附属中学初三月考）如图，抛物线C1的图象与x轴交A（−3，0），B（1，0）两点，与y轴交于点C（0，3），点D为抛物线的顶点．（1）求抛物线C1的解析式和D点坐标；（2）将抛物线C1关于点B对称后的抛物线记为C2，点E为抛物线C2的顶点，求抛物线C2的解析式和E点坐标；（3）是否在抛物线C2上存在一点P，在x轴上存在一点Q，使得以D，E，P，Q为顶点的四边形是平行四边形，若存在求出P点坐标，若不存在请说明理由．熟能生巧6．（2021·民勤县第六中学初三三模）如图，抛物线y=﹣x2+bx+c经过点A，B，C，已知点A（﹣1，0），点C（0，3）．（1）求抛物线的表达式；（2）设E是抛物线上的一点，在x轴上是否存在点F，使得A，C，E，F为顶点的四边形是平行四边形？若存在，求点F的坐标；若不存在，请说明理由．7．（2021·广州市增城区派潭镇第二中学初三期中）如图，抛物线与  轴交于A（—1，0），B（3，0），与 y 轴交于点C．已知直线过 B，C 两点．（1）求抛物线和直线BC 的表达式；（2）点 P 是抛物线上的一个动点，抛物线的对称轴 l与x 轴交于点E，过点 E作EF⊥BC，垂足为 F．点Q 是对称轴l上的一个动点，是否存在以点E，F，P，Q 为顶点的四边形是平行四边形？若存在，求出点P，Q的坐标；若不存在，请说明理由．8．（2021·河南龙亭·初三月考）综合与探究如图，抛物线经过点A(-2,0)，B(4,0)两点，与轴交于点C，点D是抛物线上一个动点，设点D的横坐标为.连接AC，BC，DB，DC，(1)求抛物线的函数表达式；(2)△BCD的面积等于△AOC的面积的时，求的值；(3)在(2)的条件下，若点M是轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M,使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由.9．（2021·四川峨眉山·初三二模）如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；10．（2021·渝中·重庆市实验学校初三月考）如图，抛物线与x轴相交于A、B两点，与y轴相交于点C．（1）若点D是抛物线对称轴上的动点，点G是抛物线上的动点，是否存在以点B、C、D、G为顶点的四边形是平行四边形．若存在，直接写出点G的坐标；若不存在，试说明理由．庖丁解牛11．（2021·辽宁顺城·初三一模）如图，抛物线y＝ax2+bx+2经过A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）P在对称轴上，Q在抛物线上，以P，Q，B，C为顶点的四边形为平行四边形，直接写出点P的坐标．