2022年广东省珠海市第八中学中考第一次模拟考试数学试题(word版含答案)

这是一份2022年广东省珠海市第八中学中考第一次模拟考试数学试题(word版含答案)，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
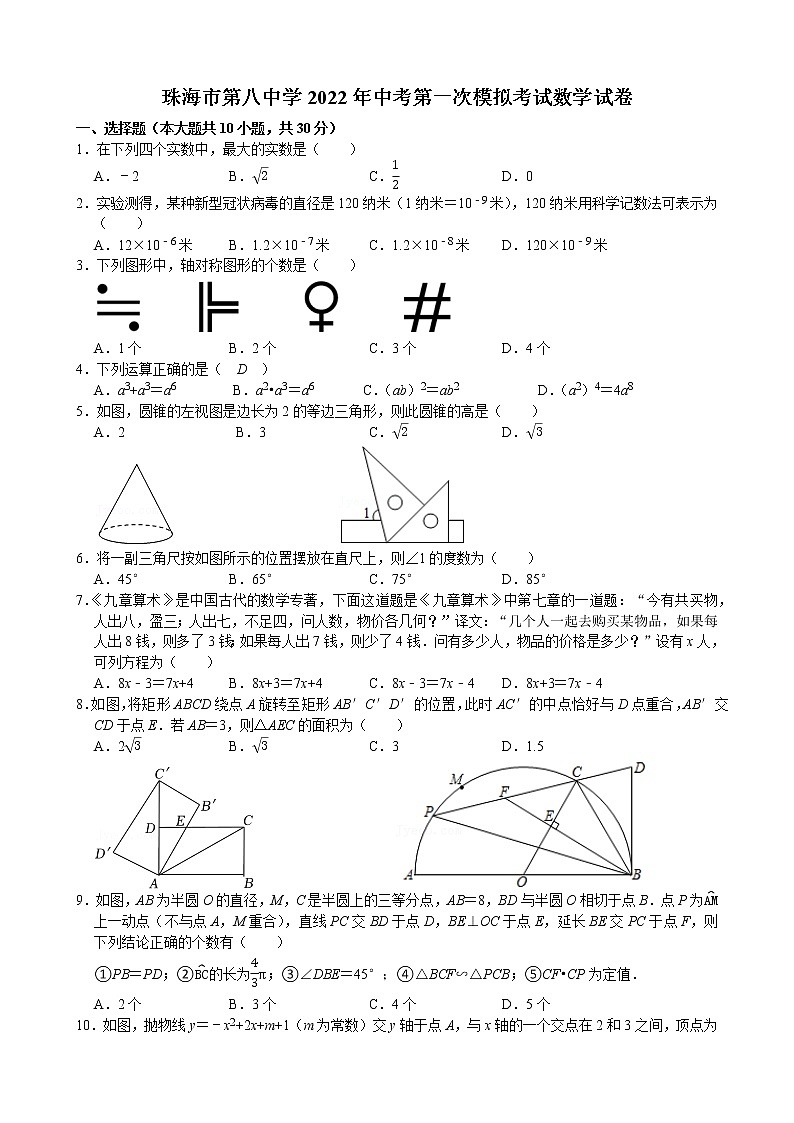
珠海市第八中学2022年中考第一次模拟考试数学试卷
一、选择题（本大题共10小题，共30分）
1．在下列四个实数中，最大的实数是（　　）
A．﹣2 B．2 C．12 D．0
2．实验测得，某种新型冠状病毒的直径是120纳米（1纳米＝10﹣9米），120纳米用科学记数法可表示为（　　）
A．12×10﹣6米 B．1.2×10﹣7米 C．1.2×10﹣8米 D．120×10﹣9米
3．下列图形中，轴对称图形的个数是（　　）

A．1个 B．2个 C．3个 D．4个
4．下列运算正确的是（　D　）
A．a3+a3＝a6 B．a2•a3＝a6 C．（ab）2＝ab2 D．（a2）4＝4a8
5．如图，圆锥的左视图是边长为2的等边三角形，则此圆锥的高是（　　）
A．2 B．3 C．2 D．3

6．将一副三角尺按如图所示的位置摆放在直尺上，则∠1的度数为（　　）
A．45° B．65° C．75° D．85°
7．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，可列方程为（　　）
A．8x﹣3＝7x+4 B．8x+3＝7x+4 C．8x﹣3＝7x﹣4 D．8x+3＝7x﹣4
8．如图，将矩形ABCD绕点A旋转至矩形AB′C′D′的位置，此时AC′的中点恰好与D点重合，AB′交CD于点E．若AB＝3，则△AEC的面积为（　　）
A．23 B．3 C．3 D．1.5

9．如图，AB为半圆O的直径，M，C是半圆上的三等分点，AB＝8，BD与半圆O相切于点B．点P为AM上一动点（不与点A，M重合），直线PC交BD于点D，BE⊥OC于点E，延长BE交PC于点F，则下列结论正确的个数有（　　）
①PB＝PD；②BC的长为43π；③∠DBE＝45°；④△BCF∽△PCB；⑤CF•CP为定值．
A．2个 B．3个 C．4个 D．5个
10．如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．
①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；
②若点M（﹣2，y1）、点N（12，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；
③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；
④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为34+2．
其中正确的判断有（　　）
A．①②③④ B．②③④ C．①③④ D．①③

二、填空题（本大题共7小题，共28分）
11．多项式3x2y2﹣12 x2y4﹣6 x3y3的公因式是 　．
12．关于x的一元二次方程x2+x﹣a＝0的一个根是2，则另一个根是 　　．
13．若分式x+1x有意义，则实数x的取值范围为 　　．
14．已知⊙O的半径是7，AB是⊙O的弦，且AB的长为73，则弦AB所对的圆周角的度数为 　　．
15．如图，一个由8个正方形组成的“C”模板恰好完全放入一个矩形框内，模板四周的直角顶点M，N，O，P，Q都在矩形ABCD的边上，若8个小正方形的面积均为1，则边AB的长为 　．
16．如图，在矩形ABCD中，AB＝3，AD＝2，以A为圆心，AD为半径作圆交AB于点E，F为DE的中点，过F作CD的平行线，交AD于点G，交BC于点H，则阴影部分的面积为　　．
17．如图，在平面直角坐标系xOy中，正方形OABC的边OC、OA分别在x轴和y轴上，OA＝10，点D是边AB上靠近点A的三等分点，将△OAD沿直线OD折叠后得到△OA′D，若反比例函数y=kx（k≠0）的图象经过A′点，则k的值为 　　．

三、解答题（本大题共3小题，共18分）
18．先化简，再求值：（xx−2+1）÷2x2−2xx2−4，其中x＝tan60°．
19．解不等式组：3(x−1)≥2x−5，①2x＜x+32，②并写出它的所有整数解．
20．已知：如图，在菱形ABCD中，E，F分别是边AD和CD上的点，且∠ABE＝∠CBF．求证：DE＝DF．

四、解答题（本大题共3小题，共24分）
21．某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于38元，经市场调查发现：该商品每天的销售量y（件）与每件售价x（元）之间符合一次函数关系，如图所示．
（1）求y与x之间的函数关系式；
（2）该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？
（3）设商场销售这种商品每天获利w（元），当每件商品的售价定为多少元时，每天销售利润最大？最大利润是多少？

22．为庆祝中国共产党建党100周年，某校加强了学生对党史知识的学习，并组织学生参加《党史知识》测试（满分100分）．为了解学生对党史知识的掌握程度，从七、八年级中各随机抽取10名学生的测试成绩，进行统计、分析，过程如下：
收集数据：
七年级：86 88 95 90 100 95 95 99 93 100
八年级：100 98 98 89 87 98 95 90 90 89
整理数据：
年级 成绩x（分）
85＜x≤90
90＜x≤95
95＜x≤100
七年级
3
4
3
八年级
5
a
b
分析数据：
年级 统计量
平均数
中位数
众数
七年级
94.1
95
d
八年级
93.4
c
98
应用数据：
（1）填空：a＝　1　，b＝　4　，c＝　92.5　，d＝　95　；
（2）若八年级共有200人参与答卷，请估计八年级测试成绩大于95分的人数；
（3）从测试成绩优秀的学生中选出5名语言表达能力较强的学生，其中八年级3名，七年级2名．现从这5名学生中随机抽取2名到当地社区担任党史宣讲员．请用画树状图或列表的方法，求恰好抽到同年级学生的概率．
23．如图，AB是⊙O的直径，点D在⊙O上，且∠AOD＝90°，点C是⊙O外一点，分别连接CA，CB、CD，CA交⊙O于点M，交OD于点N，CB的延长线交⊙O于点E，连接AD，ME，且∠ACD＝∠E．
（1）求证：CD是⊙O的切线；
（2）连接DM，若⊙O的半径为6，tanE=13，求DM的长．

五、解答题（本大题共2小题，共20分）
24．如图①，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为（﹣2，4），（﹣5，0）．将△OAB沿OA翻折，点B的对应点C恰好落在反比例函数y=kx（k≠0）的图象上．
（1）求反比例函数的表达式；
（2）如图②，将△OAB沿y轴向下平移得到△O'A'B'，设平移的距离为m（0＜m＜4），平移过程中ΔO'A'B'与△OAB重叠部分的面积为S．若点B的对应点B'恰好落在反比例函数y=kx（k≠0）的图象上，求m的值及此时S的值；
（3）如图③，连接BC交AO于点D，已知P是反比例函数y=kx（k≠0）的图象上一点，在x轴上是否存在点Q，使得以O，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点P，Q的坐标；若不存在，请说明理由．



25．如图，在平面直角坐标系中，抛物线y=−12x2+32x+2交x轴于A、B两点（点A在点B左侧），交y轴于点C，一次函数y＝kx+b（k≠0）与抛物线交于B、D两点，已知cos∠ABD=255．
（1）求点D的坐标；
（2）点F是抛物线的顶点，连接BF．P是抛物线上F、D两点之间的任意一点，过点P作PE∥BF交BD于点E，连接PF、PD、FE．求四边形PFED面积的最大值及相应的点P的坐标；
（3）连接AC，将抛物线沿射线AC方向平移55个单位长度得到新抛物线y'，新抛物线与原抛物线交于点G．S是原抛物线对称轴上一点，T是平面内任意一点，G、S、A、T四点能否构成以AS为边的菱形？若能，请直接写出点T的坐标；若不能，请说明理由．



珠海市第八中学2022年中考第一次模拟考试数学试卷
一、选择题（本大题共10小题，共30分）
1．在下列四个实数中，最大的实数是（　B　）
A．﹣2 B．2 C．12 D．0
2．实验测得，某种新型冠状病毒的直径是120纳米（1纳米＝10﹣9米），120纳米用科学记数法可表示为（　B　）
A．12×10﹣6米 B．1.2×10﹣7米 C．1.2×10﹣8米 D．120×10﹣9米
3．下列图形中，轴对称图形的个数是（　B　）

A．1个 B．2个 C．3个 D．4个
4．下列运算正确的是（　D　）
A．a3+a3＝a6 B．a2•a3＝a6 C．（ab）2＝ab2 D．（a2）4＝4a8
5．如图，圆锥的左视图是边长为2的等边三角形，则此圆锥的高是（　D　）
A．2 B．3 C．2 D．3

6．将一副三角尺按如图所示的位置摆放在直尺上，则∠1的度数为（　C　）
A．45° B．65° C．75° D．85°
7．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，可列方程为（　A　）
A．8x﹣3＝7x+4 B．8x+3＝7x+4 C．8x﹣3＝7x﹣4 D．8x+3＝7x﹣4
8．如图，将矩形ABCD绕点A旋转至矩形AB′C′D′的位置，此时AC′的中点恰好与D点重合，AB′交CD于点E．若AB＝3，则△AEC的面积为（　B　）
A．23 B．3 C．3 D．1.5

9．如图，AB为半圆O的直径，M，C是半圆上的三等分点，AB＝8，BD与半圆O相切于点B．点P为AM上一动点（不与点A，M重合），直线PC交BD于点D，BE⊥OC于点E，延长BE交PC于点F，则下列结论正确的个数有（　B　）
①PB＝PD；②BC的长为43π；③∠DBE＝45°；④△BCF∽△PCB；⑤CF•CP为定值．
A．2个 B．3个 C．4个 D．5个
10．如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．
①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；
②若点M（﹣2，y1）、点N（12，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；
③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；
④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为34+2．
其中正确的判断有（　C　）
A．①②③④ B．②③④ C．①③④ D．①③

二、填空题（本大题共7小题，共28分）
11．多项式3x2y2﹣12 x2y4﹣6 x3y3的公因式是 　3x2y2　．
12．关于x的一元二次方程x2+x﹣a＝0的一个根是2，则另一个根是 　﹣3　．
13．若分式x+1x有意义，则实数x的取值范围为 　x≥﹣1且x≠0　．
14．已知⊙O的半径是7，AB是⊙O的弦，且AB的长为73，则弦AB所对的圆周角的度数为 　60°或120°　．
15．如图，一个由8个正方形组成的“C”模板恰好完全放入一个矩形框内，模板四周的直角顶点M，N，O，P，Q都在矩形ABCD的边上，若8个小正方形的面积均为1，则边AB的长为 　201313　．
16．如图，在矩形ABCD中，AB＝3，AD＝2，以A为圆心，AD为半径作圆交AB于点E，F为DE的中点，过F作CD的平行线，交AD于点G，交BC于点H，则阴影部分的面积为　32−2　．
17．如图，在平面直角坐标系xOy中，正方形OABC的边OC、OA分别在x轴和y轴上，OA＝10，点D是边AB上靠近点A的三等分点，将△OAD沿直线OD折叠后得到△OA′D，若反比例函数y=kx（k≠0）的图象经过A′点，则k的值为 　48．　．

三、解答题（本大题共3小题，共18分）
18．先化简，再求值：（xx−2+1）÷2x2−2xx2−4，其中x＝tan60°．
解：原式=x+x−2x−2÷2x(x−1)(x+2)(x−2)=2(x−1)x−2×(x+2)(x−2)2x(x−1) =x+2x．
x＝tan60°=3，代入得：原式=3+23=1+233．
19．解不等式组：3(x−1)≥2x−5，①2x＜x+32，②并写出它的所有整数解．
解：解不等式①，得x≥﹣2，解不等式②，得x＜1，
∴不等式组的解集为﹣2≤x＜1，
∴不等式组的整数解有﹣2、﹣1、0．
20．已知：如图，在菱形ABCD中，E，F分别是边AD和CD上的点，且∠ABE＝∠CBF．求证：DE＝DF．

证明：∵四边形ABCD是菱形，∴AD＝CD，AB＝BC，∠A＝∠C，
又∵∠ABE＝∠CBF，∴△ABE≌△CBF（ASA），∴AE＝CF，∴AD﹣AE＝CD﹣CF，
∴DE＝DF．
四、解答题（本大题共3小题，共24分）
21．某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于38元，经市场调查发现：该商品每天的销售量y（件）与每件售价x（元）之间符合一次函数关系，如图所示．
（1）求y与x之间的函数关系式；
（2）该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？
（3）设商场销售这种商品每天获利w（元），当每件商品的售价定为多少元时，每天销售利润最大？最大利润是多少？

解：（1）设y与x之间的函数关系式为y＝kx+b（k≠0），由所给函数图象可知：25k+b=7035k+b=50，
解得k=−2b=120，故y与x的函数关系式为y＝﹣2x+120；
（2）根据题意，得：（x﹣20）（﹣2x+120）＝600，整理，得：x2﹣80x+1500＝0，
解得：x＝30或x＝50（不合题意，舍去），答：每件商品的销售价应定为30元；
（3）∵y＝﹣2x+120，∴w＝（x﹣20）y＝（x﹣20）（﹣2x+120）
＝﹣2x2+160x﹣2400＝﹣2（x﹣40）2+800，∵x≤38∴当x＝38时，w最大＝792，
∴售价定为38元/件时，每天最大利润w＝792元．
22．为庆祝中国共产党建党100周年，某校加强了学生对党史知识的学习，并组织学生参加《党史知识》测试（满分100分）．为了解学生对党史知识的掌握程度，从七、八年级中各随机抽取10名学生的测试成绩，进行统计、分析，过程如下：
收集数据：
七年级：86 88 95 90 100 95 95 99 93 100
八年级：100 98 98 89 87 98 95 90 90 89
整理数据：
年级 成绩x（分）
85＜x≤90
90＜x≤95
95＜x≤100
七年级
3
4
3
八年级
5
a
b
分析数据：
年级 统计量
平均数
中位数
众数
七年级
94.1
95
d
八年级
93.4
c
98
应用数据：
（1）填空：a＝　1　，b＝　4　，c＝　92.5　，d＝　95　；
（2）若八年级共有200人参与答卷，请估计八年级测试成绩大于95分的人数；
（3）从测试成绩优秀的学生中选出5名语言表达能力较强的学生，其中八年级3名，七年级2名．现从这5名学生中随机抽取2名到当地社区担任党史宣讲员．请用画树状图或列表的方法，求恰好抽到同年级学生的概率．
解：（1）a＝1，b＝4，八年级成绩按由小到大排列为：87，89，89，90，90，95，98，98，98，100，
所以八年级成绩的中位数c=90+952=92.5，七年级成绩中95出现的次数最多，则d＝95；
（2）200×410=80，估计八年级测试成绩大于95分的人数为80人；
（3）画树状图为：共有20种等可能的结果，其中两同学为同年级的结果数为8，
所以抽到同年级学生的概率=820=25．
23．如图，AB是⊙O的直径，点D在⊙O上，且∠AOD＝90°，点C是⊙O外一点，分别连接CA，CB、CD，CA交⊙O于点M，交OD于点N，CB的延长线交⊙O于点E，连接AD，ME，且∠ACD＝∠E．
（1）求证：CD是⊙O的切线；
（2）连接DM，若⊙O的半径为6，tanE=13，求DM的长．

解：（1）∵∠ACD＝∠E，∠E＝∠BAC，∴∠BAC＝∠ACD，∴AB∥CD，∴∠ODC＝∠AOD＝90°，
即OD⊥CD，∴CD是⊙O的切线；
（2）过点D作DF⊥AC于F，∵⊙O的半径为6，tanE=13=tan∠ACD＝tan∠OAN，∴ON=13OA=13×6＝2，∴DN＝OD﹣ON＝6﹣2＝4，∴CD＝3DN＝12，在Rt△CDN中，CN=DN2+CD2=42+122=410，由三角形的面积公式可得，CN•DF＝DN•CD，即410DF＝4×12，∴DF=6105，
又∵∠AMD=12∠AOD=12×90°＝45°，在Rt△DFM中，DM=2DF=2×6105=1255．
五、解答题（本大题共2小题，共20分）
24．如图①，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为（﹣2，4），（﹣5，0）．将△OAB沿OA翻折，点B的对应点C恰好落在反比例函数y=kx（k≠0）的图象上．
（1）求反比例函数的表达式；
（2）如图②，将△OAB沿y轴向下平移得到△O'A'B'，设平移的距离为m（0＜m＜4），平移过程中ΔO'A'B'与△OAB重叠部分的面积为S．若点B的对应点B'恰好落在反比例函数y=kx（k≠0）的图象上，求m的值及此时S的值；
（3）如图③，连接BC交AO于点D，已知P是反比例函数y=kx（k≠0）的图象上一点，在x轴上是否存在点Q，使得以O，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点P，Q的坐标；若不存在，请说明理由．

解：（1）∵四边形ABOC是菱形，∴AC∥BO，且A点坐标（﹣2，4），AC＝AB＝5，∴点C（3，4）．
∵点C恰好落在反比例函数y=kx（k≠0）的图象上，∴k＝3×4＝12，∴反比例函数表达式为y=12x；
（2）∵将△OAB沿y轴向下平移得到△O′A′B′，∴点B'的横坐标为﹣5，∴y=−125，
∴m=125，连接AA'，并延长AA'交BO于点E，∴AE＝4，AA'=125，∴A'E=85，
∵S△ABO=12×5×4＝10，且将△OAB沿y轴向下平移得到△O′A′B′，
∴S△A'B'O'＝10，∵BO∥B'O'，∴△ANP∽△A'B'O'，∴S△ANPS△△A'B'O'=（854）2，∴S＝10×425=85；
（3）∵四边形ABOC是菱形，∴AD＝OD，∵A（﹣2，4），点O（0，0），∴点D（﹣1，2），
若OD为边，则点P在纵坐标为2或﹣2，∴y=122=6或y=12−2=−6，∴点P（6，2）或（﹣6，﹣2），
如图3，当P（6，2）时，∵四边形ODPQ是平行四边形，∴DP＝OQ＝7，∴点Q（7，0），
如图4，当P（﹣6，﹣2）时，∵四边形ODQP是平行四边形，∴OQ与PD互相平分，
∴点H（−72，0）∴点Q（﹣7，0），若DO为对角线，∵四边形QOPD是平行四边形，
∴PQ与OD互相平分，∵OD中点坐标（−12，1），∴点P纵坐标为2，∴点P坐标为（6，2）．
∴点Q坐标为（﹣7，0）．
综上所述：当点P（6，2），点Q为（7，0）或（﹣7，0）时，以点O，D，P，Q为顶点的四边形是平行四边形，当点P（﹣6，﹣2），点Q（﹣7，0）时，以点O，D，P，Q为顶点的四边形是平行四边形．


25．如图，在平面直角坐标系中，抛物线y=−12x2+32x+2交x轴于A、B两点（点A在点B左侧），交y轴于点C，一次函数y＝kx+b（k≠0）与抛物线交于B、D两点，已知cos∠ABD=255．
（1）求点D的坐标；
（2）点F是抛物线的顶点，连接BF．P是抛物线上F、D两点之间的任意一点，过点P作PE∥BF交BD于点E，连接PF、PD、FE．求四边形PFED面积的最大值及相应的点P的坐标；
（3）连接AC，将抛物线沿射线AC方向平移55个单位长度得到新抛物线y'，新抛物线与原抛物线交于点G．S是原抛物线对称轴上一点，T是平面内任意一点，G、S、A、T四点能否构成以AS为边的菱形？若能，请直接写出点T的坐标；若不能，请说明理由．

解：（1）当y＝0时，−12x2+32x+2=0，解得x＝﹣1或x＝4，∴A（﹣1，0），B（4，0），
如图，设BD与y轴交于点G，则cos∠ABD=OBBG=255，∴4BG=255，∴BG＝25，∴OG＝3，
∴G（0，﹣2），将B，G的坐标代入直线y＝kx+b，∴4k+b=0b=−2，解得k=12b=−2，
∴直线BD的解析式为：y=12x﹣2，令12x﹣2=−12x2+32x+2，解得x＝﹣2或x＝4（舍），∴D（﹣2，﹣3）．
（2）如图，连接PB，∵PE∥BE，∴S△PBE＝S△PEF，∴S四边形PFED＝S△PED+S△PFE＝S△PED+S△PBE＝S△PBD，过点P作PH∥y轴交BD于点H，∴S△PBD=12•PH•（xB﹣xP）+12•PH•（xP﹣xD）=12•PH•（xB﹣xD），
设P（x，−12x2+32x+2），则H（x，12x﹣2），∴PH=−12x2+32x+2﹣（12x﹣2）=−12x2+x+4，
∴S四边形PFED＝S△PBD=12•PH•（xB﹣xD）=12•（−12x2+x+4）×（4+2）=−32x2+3x+12，∵−32＜0，
∴当x=32×(−32)=1时，S四边形PFED有最大值272，此时P（1，3）．
（3）存在，理由如下：当x＝0时，y＝2，∴C（0，2），∵A（﹣1，0），B（0，2），∴OA=5，
∴将抛物线沿射线AC方向平移55个单位长度，即先右平移5个单位，再向上平移10个单位，
∵点F是原抛物线的顶点，∴F（32，258），∴原抛物线的对称轴为直线x=32，设点F经过平移后移到点M（132，1058），∴平移后的抛物线y′=−12（x−132）2+1058=−12x2+132x﹣8，
令−12x2+32x+2=−12x2+132x﹣8，解得x＝2，∴G（2，3），当以点G、S、A、T以AS为边的菱形，需要分两种情况：①当AS＝AG时，如图：∵A（﹣1，0），G（2，3），∴AG＝32，设S1（32，t），
∴AG2＝（﹣1−32）2+（0﹣t）2＝18，解得t＝±472，∴S1（32，−472），S2（32，472），
∵点A（﹣1，0）到G（2，3）先向右平移3个单位，再向上平移3个单位，
∴S1（32，−472）先向右平移3个单位，再向上平移3个单位，得到T1（92，−472+3），
S2（32，472）先向右平移3个单位，再向上平移3个单位，得到T2（92，472+3）．
②当SA＝SG时，如图：设S3（32，m），∴AS32＝GS32，∴（﹣1−32）2+（0﹣m）2＝（2−32）2+（3﹣m）2，解得m=12，∴S3（32，12），∵点A（﹣1，0）和G（2，3）的中点为（12，32），
∴S3和T3的中点也为（12，32），∴T3（−12，52）．
综上所述，点T的坐标为：（92，−472+3）或（92，472+3）或（−12，52）．