2022年河南省重点中学中考数学内部摸底试卷（一）(word版含答案)

这是一份2022年河南省重点中学中考数学内部摸底试卷（一）(word版含答案)，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年河南省重点中学中考数学内部摸底试卷（一）
一、选择题（每小题3分，共30分。下列各小题均有四个答案，其中只有一个是正确的。）
1．（3分）−53的倒数是（　　）
A．−35 B．−53 C．53 D．35
2．（3分）截至2021年12月31日，河南反诈骗APP累计注册用户约为1340万，该APP能监控恶意软件，让各种骗局无处遁形．数据1340万用科学记数法表示为（　　）

A．1.34×107 B．13.4×106 C．1.34×106 D．0.134×108
3．（3分）如图所示，直线a、b被c、d所截，下列条件中能说明a∥b的是（　　）

A．∠1＝∠2 B．∠2+∠4＝180° C．∠3＝∠4 D．∠1+∠4＝180°
4．（3分）下列计算错误的是（　　）
A．a3•a2＝a5 B．a2+a4＝a6 C．（3a3）2＝9a6 D．a10÷a2＝a8
5．（3分）如图所示的几何体的三视图中有一个与其他两个不同，则不同的视图是（　　）

A．主视图 B．俯视图 C．左视图 D．右视图
6．（3分）关于x的一元二次方程x2+mx﹣m﹣1＝0的根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．有实数根 D．没有实数根
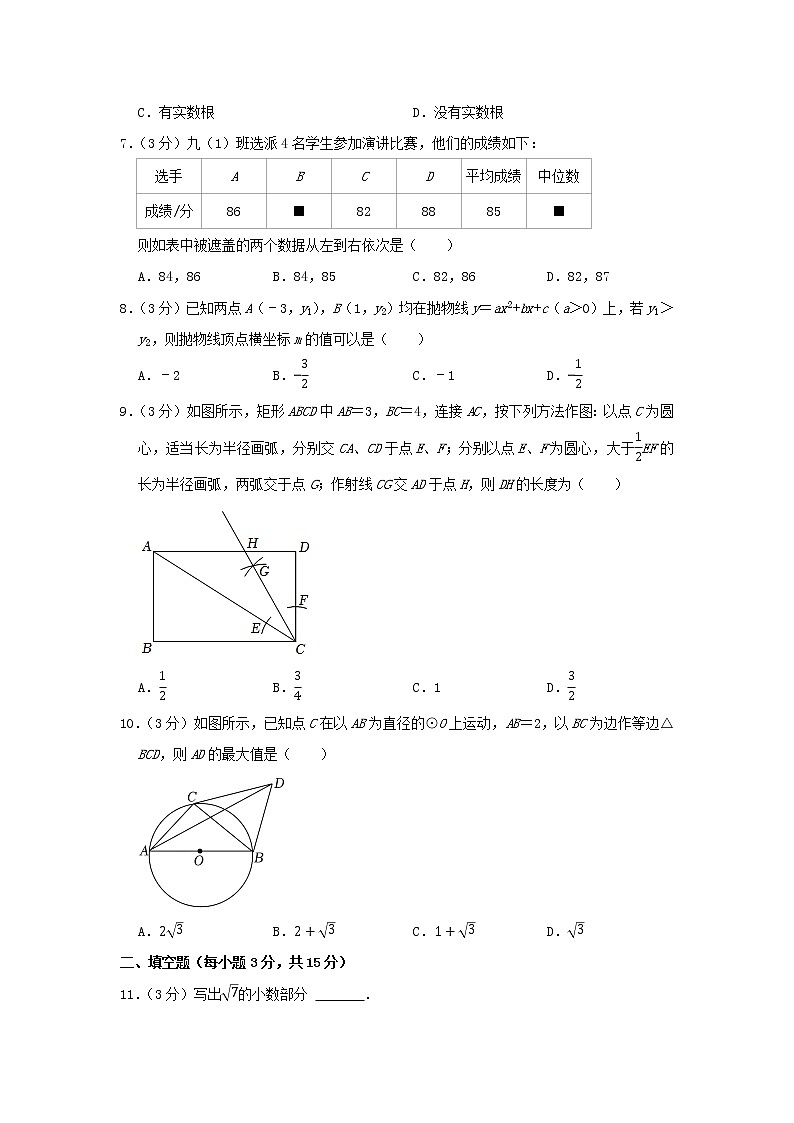
7．（3分）九（1）班选派4名学生参加演讲比赛，他们的成绩如下：
选手
A
B
C
D
平均成绩
中位数
成绩/分
86
■
82
88
85
■
则如表中被遮盖的两个数据从左到右依次是（　　）
A．84，86 B．84，85 C．82，86 D．82，87
8．（3分）已知两点A（﹣3，y1），B（1，y2）均在抛物线y＝ax2+bx+c（a＞0）上，若y1＞y2，则抛物线顶点横坐标m的值可以是（　　）
A．﹣2 B．−32 C．﹣1 D．−12
9．（3分）如图所示，矩形ABCD中AB＝3，BC＝4，连接AC，按下列方法作图：以点C为圆心，适当长为半径画弧，分别交CA、CD于点E、F；分别以点E、F为圆心，大于12EF的长为半径画弧，两弧交于点G；作射线CG交AD于点H，则DH的长度为（　　）

A．12 B．34 C．1 D．32
10．（3分）如图所示，已知点C在以AB为直径的⊙O上运动，AB＝2，以BC为边作等边△BCD，则AD的最大值是（　　）

A．23 B．2+3 C．1+3 D．3
二、填空题（每小题3分，共15分）
11．（3分）写出7的小数部分 　 　．
12．（3分）不等式组x−2≤0，3x+2＞−1的整数解的和是 　 　．
13．（3分）七巧板是我国古代劳动人民的发明之一，被誉为“东方模板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图所示是一沄用七巧板拼成的正方形，如果在此正方形中随机取一点，那么此点取自黑色部分的概率为 　 　．

14．（3分）如图所示，在矩形ABCD中，如图AB＜BC，以点C为圆心，CB的长为半径的圆分别交AD边于点E，交CD边的延长线于点F．若AE＝DF，EF的长为π，则DE的长为 　 　．

15．（3分）如图所示，正方形纸片ABCD的边长为2，点E为AD边上不与端点重合的一动点，将纸片沿过BE的直线折叠点A的落点记为F，连接CF、DF，若△CDF是以CF为腰的等腰三角形，则AE＝　 　．

三、解答题（本大题共：8个小题，满分75分）
16．（8分）先化简，再求值：(1x−1−1x+1)÷1x2+x，其中x为﹣1，0，1，2中的一个合适的数值．
17．（9分）2021年9月7日，湖南永州郡祁学校的一则视频引发热议，视频显示，为教育中学生不要浪费粮食，该校高中部校长王立新站在垃圾桶边当众吃光学生剩饭剩菜．这一举动在全国掀起了校园“光盘行动”．某校为了让该校学生理解这次活动的重要性，校政教处在某天午餐后，随机调查部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．

（1）这次被调查的同学共有 　 　名；
（2）把条形统计图补充完整；
（3）若政教处准备从九（2）班就餐光盘的2男1女三名学生中随机抽取两人进行菜品调研，问恰巧抽到1男1女的概率为多少？
18．（9分）由绿地集团耗资22亿建设的“大玉米”位于河南省省会郑州市郑东新区，因为其是圆柱塔式建筑，夜晚其布景灯采用黄色设计，因此得名，如今已经成为CBD的一座新地标建筑．某数学兴趣小组为测量其高度，一人先在附近一楼房的底端A点处观测“大玉米”顶端C处的仰角是45°，然后爬到该楼房顶端B点处观测“大玉米”底部D处的俯角是30°．已知楼房AB高约是162m，根据以上观测数据求“大玉米”的高．（结果保留整数，参考数据：2≈1.41，3≈1.73）

19．（9分）如图所示，一次函数y＝kx+b的图象与反比例函数y=mx的图象相交于两点A（1，n），B（﹣2，﹣1），与y轴相交于点C．
（1）求反比例函数和一次函数解析式；
（2）直接写出：不等式kx+b＞mx＞0的解集是 　 　；
（3）依据相关数据求△AOB的面积．

20．（9分）2021年的冬天来得比往年更早一些．蛰居在家的电脑族饱受冰冷之苦，某商家瞅准商机计划购进甲、乙两款电热鼠标垫，已知购进甲鼠标垫2个和乙鼠标垫1个共需130元；购进甲鼠标垫1个和乙鼠标垫2个共需170元．
（1）求甲、乙两款鼠标垫每个的进价分别是多少元？
（2）商场决定甲鼠标垫以每个40元出售，乙鼠标垫以每个90元出售，为满足市场需求，需购进甲、乙两款鼠标垫共80个，且甲款鼠标垫的数量不少于乙款鼠标垫数量的4倍，请你求出获利最大的进货方案，并求出最大利润．

21．（10分）阅读：如图1所示，四边形ABCD是⊙O的内接四边形，连接AC、BD．BC是⊙O的直径，AB＝AC．请说明线段AD、BD、CD之间的数量关系．下面是王林解答该问题的部分解答过程，请补充完整：
解：2AD+CD＝BD．
理由如下：∵BC是⊙O的直径，∴∠BAC＝90°．
∵AB＝AC，∴∠ABC＝∠ACB＝45°．
如图2所示，过点A作AM⊥AD交BD于点M，…
解答：（1）补全王林的解答过程；
（2）如图3所示，四边形ABCD中∠ABC＝30°，连接AC、BD．若∠BAC＝∠BDC＝90°，直接写出线段AD、BD、CD之间的关系式是 　 　．


22．（10分）已知二次函数y＝x2﹣2mx+m2﹣4的图象与x轴交于A、B两点（点A在点B的左边），且与y轴交于D点．
（1）当点B、D都在坐标系的正半轴，且△BOD为等腰三角形，求二次函数解析式；
（2）当m＝﹣2时，将函数y＝x2﹣2mx+m2﹣4的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象Ω．当直线y＝2x+n与图象Ω仅有两个公共点时，求实数n的取值范围．
23．（11分）【问题发现】
（1）如图1所示，△ABC和△ADE均为正三角形，B、D、E三点共线．猜想线段BD、CE之间的数量关系为 　 　；∠BEC＝　 　°；
【类比探究】
（2）如图2所示，△ABC和△ADE均为等腰直角三角形，∠ACB＝∠AED＝90°，AC＝BC，AE＝DE，其他条件同（1），请问（1）中的结论还成立吗？说明你的理由；
【拓展延伸】
（3）如图3所示，在△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，DE为△ABC的中位线，将△CDE绕点C旋转，当DE所在直线经过点A时，求BE的长．（直接写出答案）



2022年河南省重点中学中考数学内部摸底试卷（一）
教师解析版
一、选择题（每小题3分，共30分。下列各小题均有四个答案，其中只有一个是正确的。）
1．（3分）−53的倒数是（　　）
A．−35 B．−53 C．53 D．35
【分析】根据倒数的定义进行计算即可．
【解答】解：因为（−53）×（−35）＝1，
所以−53的倒数是−35，
故选：A．
2．（3分）截至2021年12月31日，河南反诈骗APP累计注册用户约为1340万，该APP能监控恶意软件，让各种骗局无处遁形．数据1340万用科学记数法表示为（　　）

A．1.34×107 B．13.4×106 C．1.34×106 D．0.134×108
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数，当原数绝对值＜1时，n是负整数．
【解答】解：1340万＝13400000＝1.34×107．
故选：A．
3．（3分）如图所示，直线a、b被c、d所截，下列条件中能说明a∥b的是（　　）

A．∠1＝∠2 B．∠2+∠4＝180° C．∠3＝∠4 D．∠1+∠4＝180°
【分析】根据平行线的判定定理求解即可．
【解答】解：∵∠3＝∠4，
∴a∥b（同位角相等，两直线平行），
故选：C．
4．（3分）下列计算错误的是（　　）
A．a3•a2＝a5 B．a2+a4＝a6 C．（3a3）2＝9a6 D．a10÷a2＝a8
【分析】按照整式幂的运算法则逐一计算辨别即可．
【解答】解：∵a3•a2＝a5，
∴选项A不符合题意；
∵a2与a4＝不是同类项，
∴a2+a4不能计算，
∴选项B符合题意；
∵（3a3）2＝9a6，
∴选项C不符合题意；
∵a10÷a2＝a8，
∴选项D不符合题意；
故选：B．
5．（3分）如图所示的几何体的三视图中有一个与其他两个不同，则不同的视图是（　　）

A．主视图 B．俯视图 C．左视图 D．右视图
【分析】判断出组合体的左视图、主视图及俯视图，即可作出判断．
【解答】解：几何体的左视图和主视图是相同（底层是三个小正方形，上层的右边是一个小正方形），则不同的视图是俯视图，俯视图有三列，从左到右小正方形的个数分别为3、1、1．
故选：B．
6．（3分）关于x的一元二次方程x2+mx﹣m﹣1＝0的根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．有实数根 D．没有实数根
【分析】根据方程的系数结合根的判别式即可得出：Δ＝m2﹣4×（﹣m﹣1）＝（m+2）2≥0，即可判定方程有实数根．
【解答】解：∵Δ＝m2﹣4×（﹣m﹣1）＝（m+2）2≥0，
∴关于x的一元二次方程x2+mx﹣m﹣1＝0有两个实数根．
故选：C．
7．（3分）九（1）班选派4名学生参加演讲比赛，他们的成绩如下：
选手
A
B
C
D
平均成绩
中位数
成绩/分
86
■
82
88
85
■
则如表中被遮盖的两个数据从左到右依次是（　　）
A．84，86 B．84，85 C．82，86 D．82，87
【分析】根据中位数和平均数的求解即可．
【解答】解：根据题意可得：B的成绩＝85×4﹣86﹣82﹣88＝84，
中位数为85，
故选：B．
8．（3分）已知两点A（﹣3，y1），B（1，y2）均在抛物线y＝ax2+bx+c（a＞0）上，若y1＞y2，则抛物线顶点横坐标m的值可以是（　　）
A．﹣2 B．−32 C．﹣1 D．−12
【分析】由抛物线开口方向可得与抛物线对称轴距离越近的点的纵坐标越小，根据点A，B的横坐标求解．
【解答】解：∵a＞0，
∴抛物线开口向上，
∴与抛物线对称轴距离越近的点的纵坐标越小，
∵y1＞y2，
∴点B与对称轴的距离大于点A与对称轴的距离，
故选：D．
9．（3分）如图所示，矩形ABCD中AB＝3，BC＝4，连接AC，按下列方法作图：以点C为圆心，适当长为半径画弧，分别交CA、CD于点E、F；分别以点E、F为圆心，大于12EF的长为半径画弧，两弧交于点G；作射线CG交AD于点H，则DH的长度为（　　）

A．12 B．34 C．1 D．32
【分析】过H点作HM⊥AC于M，如图，根据基本作图得到CH平分∠ACD，则利用角平分线的性质得到HM＝HD，接着根据勾股定理计算出AC＝15，通过证明Rt△CHD≌Rt△CHM得到CD＝CM＝3，所以AM＝2，设DH＝t，则AH＝4﹣t，HM＝t，利用勾股定理得到t2+22＝（4﹣t）2，解方程得到HD＝1.5，从而得到H点的横坐标．
【解答】解：如图，过H点作HM⊥AC于M，

由作法得CH平分∠ACD，
∵HM⊥AC，HD⊥CD，
∴HM＝HD，
∵矩形ABCD的顶点A的坐标为（﹣2，3），C点坐标为（2，0），
∴AB＝3，BC＝2OB＝2OC＝4，
在Rt△ABC中，AC=AB2+BC2=32+42=5，
在Rt△CHD和Rt△CHM中，
CH=CHHD=HM，
∴Rt△CHD≌Rt△CHM（HL），
∴CD＝CM＝3，
∴AM＝AC﹣CM＝5﹣3＝2，
设DH＝t，则AH＝4﹣t，HM＝t，
在Rt△AHM中，t2+22＝（4﹣t）2，解得t＝1.5，
即HD＝1.5，
故选：D．
10．（3分）如图所示，已知点C在以AB为直径的⊙O上运动，AB＝2，以BC为边作等边△BCD，则AD的最大值是（　　）

A．23 B．2+3 C．1+3 D．3
【分析】将△ABD绕点B逆时针旋转60°，则点D的对应点与点C重合，得到△EBC，连接OC、OE、AE，当点C、点O、点E在同一条直线上时，CE的值最大，此时AD的值最大，根据勾股定理求得OE=3，而OC＝1，可知CE的最大值为1+3．
【解答】解：如图1，∵△BCD是等边三角形，
∴BC＝BD，∠CBD＝60°，
将△ABD绕点B逆时针旋转60°，则点D的对应点与点C重合，得到△EBC，连接OC、OE、AE，
∵△EBC≌△ABD，
∴EB＝AB＝2，
∵∠ABE＝60°，
∴△ABE是等边三角形，
∵OA＝OB＝1，
∴OE⊥AB，
∴∠BOE＝90°，
∴OE=EB2−OB2=22−12=3，
∵EC≤OC+OE，且OC＝OB＝1，
∴EC≤1+3，
当点C、点O、点E在同一条直线上时，如图2，此时EC的值最大，EC＝1+3，
∵AD＝EC，
∴AD的最大值是1+3，
故选：C．

二、填空题（每小题3分，共15分）
11．（3分）写出7的小数部分 　7−2　．
【分析】估算出7的值即可解答．
【解答】解：∵2＜7＜3，
∴7的小数部分为7−2，
故答案为：7−2．
12．（3分）不等式组x−2≤0，3x+2＞−1的整数解的和是 　3　．
【分析】先解出每个不等式的解集，即可得到不等式组的解集，然后写出该不等式组的所有整数解，再相加即可．
【解答】解：x−2≤0①3x+2＞−1②，
由不等式①，得：x≤2，
由不等式②，得：x＞﹣1，
故原不等式组的解集是﹣1＜x≤2，
∴该不等式组的整数解是0，1，2，
∵0+1+2＝3，
∴不等式组x−2≤0，3x+2＞−1的整数解的和是3，
故答案为：3．
13．（3分）七巧板是我国古代劳动人民的发明之一，被誉为“东方模板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图所示是一沄用七巧板拼成的正方形，如果在此正方形中随机取一点，那么此点取自黑色部分的概率为 　38　．

【分析】首先设设正方形的面积，再表示出阴影部分面积，然后可得概率．
【解答】解：设“东方模板”的面积为4，则阴影部分三角形面积为1，平行四边形面积为12，
则点取自黑色部分的概率为：1+124=38，
故答案为：38．
14．（3分）如图所示，在矩形ABCD中，如图AB＜BC，以点C为圆心，CB的长为半径的圆分别交AD边于点E，交CD边的延长线于点F．若AE＝DF，EF的长为π，则DE的长为 　22　．

【分析】连接CE，则CB＝CE＝CF 设CB＝R，则CE＝CF＝DA，推出DCE＝45°，根据弧长公式求出R，然后求出DE＝CE•sin 45°＝4×22B＝22．
【解答】解：连接CE，则CB＝CE＝CF，
设CB＝R，
∵四边形ABCD是矩形，
∴CE＝CF＝DA，
∵AE＝DF，
∴DE＝DC，
∴DCE＝45°，
∵EF的长为π，
∴45πR180=π，
解得R＝4，
在Rt△DCE中，
DE＝CE•sin 45°＝4×22B＝22．
故答案为：22．

15．（3分）如图所示，正方形纸片ABCD的边长为2，点E为AD边上不与端点重合的一动点，将纸片沿过BE的直线折叠点A的落点记为F，连接CF、DF，若△CDF是以CF为腰的等腰三角形，则AE＝　233或4﹣23　．

【分析】分两种情况：①当FC＝FD时，如图3，作辅助线，构建直角三角形，利用30°角的特殊三角函数值求得AE的长；
②当FC＝DC时，如图4，作辅助线，构建直角三角形，设未知数，根据勾股定理列方程可求得AE的长．
【解答】解：当△CDF是以CF为腰的等腰三角形时，分两种情况：
①当FC＝FD时，如图，过F作FM⊥AB于M，交CD于点N，
∵四边形ABCD是正方形，
∴AB∥CD，
∴FN⊥CD，
∵FC＝FD，
∴MN是正方形的对称轴，
如图，连接AF，

∴FA＝FB＝2，
∵AB＝2，
∴△ABF是等边三角形，
∴∠ABF＝60°，
由折叠得：∠ABE＝∠EBF=12∠ABF＝30°，
∴AE＝tan30°•AB=33×2=233；
②当FC＝DC时，如图，过F作FG⊥AD，交AD于G，交BC于H，

∵AD∥BC，
∴GH⊥BC，
∵AB＝BF，AB＝CD，
∴BF＝FC，
∴BH＝CH＝1，
由勾股定理得：FH=BF2−BH2=22−12=3，
∵∠A＝∠ABG＝∠BGH＝90°，
∴四边形ABGH为矩形，
∴GH＝AB＝2，AG＝BH＝1，
∴FG＝GH﹣FH＝2−3，
设AE＝x，则EF＝x，EG＝AG﹣AE＝1﹣x，
由勾股定理得：x2＝（1﹣x）2+（2−3）2，
∴x＝4﹣23，
∴AE＝4﹣23，
综上所述，AE的长为233或4﹣23．
故答案为：233或4﹣23．
三、解答题（本大题共：8个小题，满分75分）
16．（8分）先化简，再求值：(1x−1−1x+1)÷1x2+x，其中x为﹣1，0，1，2中的一个合适的数值．
【分析】括号内先通分后计算，然后将除法转化为乘法计算，再选择合适的x代入求值即可．
【解答】解：原式=[x+1(x+1)(x−1)−x−1(x+1)(x−1)]⋅x(x+1)
=2(x+1)(x−1)⋅x(x+1)
=2xx−1．
根据分式有意义的条件可得x＝2．
∴原式=2×22−1=4．
17．（9分）2021年9月7日，湖南永州郡祁学校的一则视频引发热议，视频显示，为教育中学生不要浪费粮食，该校高中部校长王立新站在垃圾桶边当众吃光学生剩饭剩菜．这一举动在全国掀起了校园“光盘行动”．某校为了让该校学生理解这次活动的重要性，校政教处在某天午餐后，随机调查部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．

（1）这次被调查的同学共有 　100　名；
（2）把条形统计图补充完整；
（3）若政教处准备从九（2）班就餐光盘的2男1女三名学生中随机抽取两人进行菜品调研，问恰巧抽到1男1女的概率为多少？
【分析】（1）由“光盘”的人数及其所占百分比可得答案；
（2）总人数减去其它三个类型人数即可求出“少量”的人数，从而补全图形；
（3）画树状图展示所有12种等可能的结果数，再找出恰好抽到的两名学生恰为1男1女的结果数，然后根据概率公式求解．
【解答】解：（1）这次被调查的同学共有40÷40%＝100（名），
故答案为：100；

（2）剩少量的人数是；100﹣40﹣25﹣15＝20（名），
把条形统计图补充完整如下；


（3）画树状图如图：

共有6种等可能结果，其中抽到的两名学生恰为1男1女的情况有4种，
∴抽到的两名学生恰为1男1女的概率为46=23．
18．（9分）由绿地集团耗资22亿建设的“大玉米”位于河南省省会郑州市郑东新区，因为其是圆柱塔式建筑，夜晚其布景灯采用黄色设计，因此得名，如今已经成为CBD的一座新地标建筑．某数学兴趣小组为测量其高度，一人先在附近一楼房的底端A点处观测“大玉米”顶端C处的仰角是45°，然后爬到该楼房顶端B点处观测“大玉米”底部D处的俯角是30°．已知楼房AB高约是162m，根据以上观测数据求“大玉米”的高．（结果保留整数，参考数据：2≈1.41，3≈1.73）

【分析】在Rt△ABD中由边角关系求出AD的长，在Rt△ACD中，求出CD即可．
【解答】解：由题意可知，∠CAD＝45°，∠EBD＝30°＝∠ADB，AB＝DE＝162米，
在Rt△ABD中，∵tan30°=ABAD，
∴AD=16233=1623（米），
在Rt△ACD中，∠CAD＝45°，
∴CD＝AD＝1623≈280（米），
答：“大玉米”的高约为280米．

19．（9分）如图所示，一次函数y＝kx+b的图象与反比例函数y=mx的图象相交于两点A（1，n），B（﹣2，﹣1），与y轴相交于点C．
（1）求反比例函数和一次函数解析式；
（2）直接写出：不等式kx+b＞mx＞0的解集是 　x＞1　；
（3）依据相关数据求△AOB的面积．

【分析】（1）用待定系数法先求出反比例函数的解析式，再求出A点坐标，再将A，B点坐标代入一次函数求解即可；
（2）根据图象即可得出不等式的解集；
（3）先求出C点坐标，再分别求出△AOC和△BOC的面积即可求出△AOB的面积．
【解答】解：（1）∵反比例函数y=mx的图象过B（﹣2，﹣1），
∴m＝（﹣2）×（﹣1）＝2，
∴反比例函数的解析式为：y=2x，
∵点A（1，n）在反比例函数图象上，
∴1×n＝2，
∴n＝2，
∴点A的坐标为（1，2），
将点A，B坐标代入一次函数y＝kx+b中，
得k+b=2−2k+b=−1，
解得k=1b=1，
∴一次函数的解析式为：y＝x+1．
（2）根据图象可知，不等式kx+b＞mx＞0的解集是：x＞1．
故答案为：x＞1．
（3）过点A作AG⊥y轴于点G，过点B作BH⊥y轴于点H，如下图所示：

∵一次函数y＝x+1与y轴相交于点C，
∴C点坐标为（0，1），
∴OC＝1，
∵A点坐标为（1，2），
∴AG＝1，
∵B点坐标为（﹣2，﹣1），
∴BH＝2，
∴S△AOB＝S△AOC+S△BOC=1×12+1×22=32．
20．（9分）2021年的冬天来得比往年更早一些．蛰居在家的电脑族饱受冰冷之苦，某商家瞅准商机计划购进甲、乙两款电热鼠标垫，已知购进甲鼠标垫2个和乙鼠标垫1个共需130元；购进甲鼠标垫1个和乙鼠标垫2个共需170元．
（1）求甲、乙两款鼠标垫每个的进价分别是多少元？
（2）商场决定甲鼠标垫以每个40元出售，乙鼠标垫以每个90元出售，为满足市场需求，需购进甲、乙两款鼠标垫共80个，且甲款鼠标垫的数量不少于乙款鼠标垫数量的4倍，请你求出获利最大的进货方案，并求出最大利润．

【分析】（1）设甲、乙两种鼠标垫每个进价分别是x元、y元，购进甲鼠标垫2个和乙鼠标垫1个共需130元；购进甲鼠标垫1个和乙鼠标垫2个共需170元列方程组，求解即可；
（2）根据题意可以得到利润与购买甲款鼠标的函数关系式，根据函数的性质以及A的取值范围求最大值即可．
【解答】解：（1）设甲、乙两种鼠标垫每个进价分别是x元、y元根据题意，
得2x+y=130x+2y=170，
解得：x=30y=70，
即甲、乙两款鼠标垫每件的进价分别是30元、70元；
（2）设购买甲种鼠标垫a个，获利为w元，
w＝（40﹣30）a+（90﹣70）（80﹣a）＝﹣10a+1600，
∵a≥4（80﹣a），
解得：a≥64，
又∵﹣10＜0，
∴当a＝64时，w取得最大值，此时w＝1600﹣640＝960．
即获利最大的进货方案是购买甲款鼠标垫64个，乙款鼠标垫16个，最大利润是960元．
21．（10分）阅读：如图1所示，四边形ABCD是⊙O的内接四边形，连接AC、BD．BC是⊙O的直径，AB＝AC．请说明线段AD、BD、CD之间的数量关系．下面是王林解答该问题的部分解答过程，请补充完整：
解：2AD+CD＝BD．
理由如下：∵BC是⊙O的直径，∴∠BAC＝90°．
∵AB＝AC，∴∠ABC＝∠ACB＝45°．
如图2所示，过点A作AM⊥AD交BD于点M，…
解答：（1）补全王林的解答过程；
（2）如图3所示，四边形ABCD中∠ABC＝30°，连接AC、BD．若∠BAC＝∠BDC＝90°，直接写出线段AD、BD、CD之间的关系式是 　2AD+3CD＝BD　．


【分析】（1）作MA⊥AD，AM交BD于M，求出∠BAM＝∠DAC＝90°﹣∠MAC，根据圆周角定理求出∠ABM＝∠ACD，根据全等三角形的判定得出△ABM≌△ACD，根据全等三角形的性质得出AM＝AD，BM＝CD，再求出答案即可；
（2）作MA⊥AD，AM交BD于M，求出∠BAM＝∠DAC＝90°﹣∠MAC，根据圆周角定理得出∠ABM＝∠ACD，根据相似三角形的判定得出△ABM∽△ACD，根据相似三角形的性质得出AMAD=BMCD=ABAC=3ACAC=3，，求出AM=3AD，BM=3CD，根据勾股定理求出DM＝2AD，再求出答案即可．
【解答】解：（1）∵∠BAC＝∠MAD＝90°，
∴∠BAM＝∠DAC＝90°﹣∠MAC，
∵∠ABM和∠ACD都是AD对的圆周角，
∴∠ABM＝∠ACD，
在△ABM和△ACD中，
∠ABM=∠ACDAB=AC∠BAM=∠DAC，
∴△ABM≌△ACD（ASA），
∴AM＝AD，BM＝CD，
∴△MAD是等腰直角三角形，
∴MD=2AD，
∴BD＝BM+DM＝CD+2AD，即2AD+CD＝BD；
（2）2AD+3CD＝BD．
由∠BAC＝∠BDC＝90°，易得四点共圆，
作MA⊥AD交BD于M，

∴∠BAM＝∠DAC＝90°﹣∠MAC，
∵∠ABC＝30°，∠BAC＝90°，
∴BC＝2AC，AB=3AC，
∵∠ABM和∠ACD都是AD对的圆周角，
∴∠ABM＝∠ACD，
∵∠BAM＝∠DAC，
∴△ABM∽△ACD，
∴AMAD=BMCD=ABAC=3ACAC=3，
即AM=3AD，BM=3CD，
在Rt△MAD中，由勾股定理得：DM=AD2+(3AD)2=2AD，
∴BD＝BM+DM=3CD+2AD，即2AD+3CD＝BD，
故答案为：2AD+3CD＝BD．
22．（10分）已知二次函数y＝x2﹣2mx+m2﹣4的图象与x轴交于A、B两点（点A在点B的左边），且与y轴交于D点．
（1）当点B、D都在坐标系的正半轴，且△BOD为等腰三角形，求二次函数解析式；
（2）当m＝﹣2时，将函数y＝x2﹣2mx+m2﹣4的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象Ω．当直线y＝2x+n与图象Ω仅有两个公共点时，求实数n的取值范围．
【分析】（1）令y＝0求得方程的两个解，即得出A、B、D的坐标；再根据点D在y轴正半轴，分情况讨论，从而得出m的值，最后写出二次函数解析式；
（2）由已知条件，得出A、B的坐标，即得出抛物线的顶点，由直线与图象的交点个数求出b的不同值，再得出n的取值范围即可．
【解答】解：（1）令y＝0得x2﹣2mx+m2﹣4＝0，解得x1＝m﹣2，x2＝m+2，
∴A（m﹣2，0），B（m+2，0），D（0，m2﹣4），
∵点D在y轴正半轴，
∴m2﹣4＞0，设存在实数m，使得△BOD为等腰三角形，则BO＝OD，
即|m+2|＝m2﹣4，
①当m+2＞0时，m2﹣4＝m+2，解得m＝3或m＝﹣2（舍去）；
②当m+2＜0时，m2﹣4+m+2＝0，解得m＝1或m＝﹣2（都舍去）；
③当m+2＝0时，点O、B、D重合，不合题意，舍去；
综上所述，m＝3．
故二次函数解析式为：y＝x2﹣6x+5．
（2）当m＝﹣2时，y＝x2+4x，则A（﹣4，0），B（0，0）顶点为（﹣2，﹣4），
因为直线y＝2x+n与图象Ω有两个公共点，
则当直线y＝2x+n过A点时n＝8，
当直线y＝2x+n过B（0，0）时，n＝0，
当直线y＝2x+n与y＝﹣x2﹣4x只有一个公共点时，n＝9，
根据图象，可得0＜n＜8或n＞9．
23．（11分）【问题发现】
（1）如图1所示，△ABC和△ADE均为正三角形，B、D、E三点共线．猜想线段BD、CE之间的数量关系为 　BD＝CE　；∠BEC＝　60　°；
【类比探究】
（2）如图2所示，△ABC和△ADE均为等腰直角三角形，∠ACB＝∠AED＝90°，AC＝BC，AE＝DE，其他条件同（1），请问（1）中的结论还成立吗？说明你的理由；
【拓展延伸】
（3）如图3所示，在△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，DE为△ABC的中位线，将△CDE绕点C旋转，当DE所在直线经过点A时，求BE的长．（直接写出答案）


【分析】（1）证△ABD≌△ACE，得BD＝CE，∠BDA＝∠CEA，进而判断出∠BEC的度数为60°即可；
（2）证△ABD∽△ACE，得∠ADB＝∠AEC＝135°，BDCE=ABAC=ADAE，则∠BEC＝∠AEC﹣∠AED＝45°，再求出BDCE=ABAC=2，即可得出结论；
（3）分两种情况，根据相似三角形的判定与性质结合勾股定理分别求出BE的长即可．
【解答】解：（1）∵△ACB和△ADE均为等边三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∠ADE＝∠AED＝60°，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
即∠BAD＝∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴△ABD≌△ACE（SAS），
∴BD＝CE，∠BDA＝∠CEA，
∵点B，D，E在同一直线上，
∴∠ADB＝180﹣60＝120°，
∴∠AEC＝120°，
∴∠BEC＝∠AEC﹣∠AED＝120﹣60＝60°，
综上所述，∠BEC的度数为60°，线段BD与CE之间的数量关系是BD＝CE，
故答案为：BD＝CE，60．
（2）不成立，BD=2CE，∠BEC＝45°，理由如下：
∵△ABC和△ADE均为等腰直角三角形，
∴∠BAC＝∠ABC＝∠ADE＝∠DAE＝45°，∠ACB＝∠AED＝90°，
∴∠BAD＝∠CAE，∠ADB＝135°，
∵Rt△ABC和Rt△ADE中，sin∠ABC=ACAB，sin∠ADE=AEAD，sin45°=22，
∴ACAB=AEAD=22，
∴ABAD=ACAE，
又∵∠BAD＝∠CAE，
∴△ABD∽△ACE，
∴∠ADB＝∠AEC＝135°，BDCE=ABAC=ADAE，
∴∠BEC＝∠AEC﹣∠AED＝45°，
∵ACAB=AEAD=22，
∴ABAC=2，
∴BDCE=ABAC=2，
∴BD=2CE；
（3）分两种情况：
①如图4，∵∠ACB＝90°，∠A＝30°，AB＝4，
∴BC=12AB＝2，
∴AC=AB2−BC2=42−22=23，
∵DE为△ABC的中位线，
∴DE=12AB＝2，DE∥AB，CE=12BC，CD=12AC，
∴∠CDE＝∠A＝30°，CDAC=CEBC=12，
由旋转的性质得：∠ACD＝∠BCE，
∴△ACD∽△BCE，
∴ADBE=ACBC=232=3，∠ADC＝∠BEC＝180°﹣∠CDE＝150°，
∵∠CED＝90°﹣∠CDE＝60°，
∴∠AEB＝∠BEC﹣∠CED＝150°﹣60°＝90°，
设BE＝x，则AD=3x，AE＝AD+DE=3x+2，
在Rt△ABE中，由勾股定理得：x2+（3x+2）2＝42，
解得：x=15−32或x=−15−32（舍去），
∴BE=15−32；
②如图5，同①得：△ACD∽△BCE，
则ADBE=ACBC=232=3，∠AEB＝90°，
设BE＝y，则AD=3y，AE＝AD﹣DE=3y﹣2，
在Rt△ABE中，由勾股定理得：y2+（3y﹣2）2＝42，
解得：y=15+32或y=−15+32（舍去），
∴BE=15+32；
综上所述，BE的长为15−32或15+32．