2022北京中考数学一轮复习系列系列——圆（学生版）

这是一份2022北京中考数学一轮复习系列系列——圆（学生版），共29页。试卷主要包含了已知锐角∠AOB，如图，，已知等内容，欢迎下载使用。
2022年北京中考数学一轮复习系列系列——（07）圆
五年中考
一．选择题（共1小题）
1．已知锐角∠AOB，如图，
（1）在射线OA上取一点C，以点O为圆心，OC长为半径作，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；
（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（　　）

A．∠COM＝∠COD B．若OM＝MN．则∠AOB＝20°
C．MN∥CD D．MN＝3CD
二．填空题（共4小题）
2．如图，PA，PB是⊙O的切线，A，B是切点．若∠P＝50°，则∠AOB＝　 　．






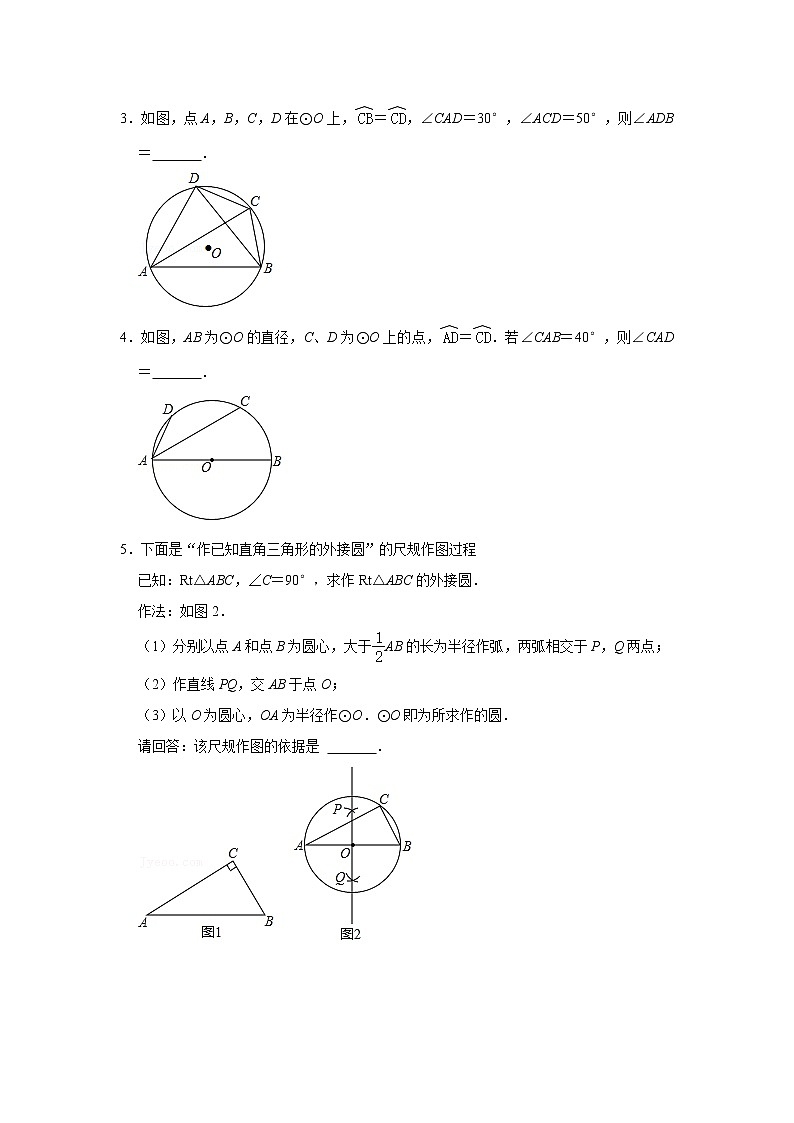
3．如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝　 　．

4．如图，AB为⊙O的直径，C、D为⊙O上的点，＝．若∠CAB＝40°，则∠CAD＝　 　．

5．下面是“作已知直角三角形的外接圆”的尺规作图过程
已知：Rt△ABC，∠C＝90°，求作Rt△ABC的外接圆．
作法：如图2．
（1）分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于P，Q两点；
（2）作直线PQ，交AB于点O；
（3）以O为圆心，OA为半径作⊙O．⊙O即为所求作的圆．
请回答：该尺规作图的依据是 　 　．



三．解答题（共6小题）
6．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E．
（1）求证：∠BAD＝∠CAD；
（2）连接BO并延长，交AC于点F，交⊙O于点G，连接GC．若⊙O的半径为5，OE＝3，求GC和OF的长．

7．已知：如图，△ABC为锐角三角形，AB＝AC，CD∥AB．
求作：线段BP，使得点P在直线CD上，且∠ABP＝∠BAC．
作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；
②连接BP．
线段BP就是所求作的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∵CD∥AB，
∴∠ABP＝　 　．
∵AB＝AC，
∴点B在⊙A上．
又∵点C，P都在⊙A上，
∴∠BPC＝∠BAC（ 　 　）（填推理的依据）．
∴∠ABP＝∠BAC．

8．如图，AB为⊙O的直径，C为BA延长线上一点，CD是⊙O的切线，D为切点，OF⊥AD于点E，交CD于点F．
（1）求证：∠ADC＝∠AOF；
（2）若sinC＝，BD＝8，求EF的长．

9．在平面内，给定不在同一条直线上的点A，B，C，如图所示，点O到点A，B，C的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G，∠ABC的平分线交图形G于点D，连接AD，CD．
（1）求证：AD＝CD；
（2）过点D作DE⊥BA，垂足为E，作DF⊥BC，垂足为F，延长DF交图形G于点M，连接CM．若AD＝CM，求直线DE与图形G的公共点个数．

10．如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．
（1）求证：OP⊥CD；
（2）连接AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求OP的长．



11．如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．
（1）求证：DB＝DE；
（2）若AB＝12，BD＝5，求⊙O的半径．

三年模拟
一．选择题（共9小题）
1．如图，AB是⊙O直径，点C，D将分成相等的三段弧，点P在上．已知点Q在上且∠APQ＝115°，则点Q所在的弧是（　　）

A． B． C． D．
2．如图，PA，PB是⊙O的切线，切点分别为A，B，PO的延长线交⊙O于点C，连接OA，OB，BC．若AO＝2，OP＝4，则∠C等于（　　）

A．20° B．30° C．45° D．60°
3．一个圆锥的侧面展开图是圆心角为120°，半径为3的扇形，这个圆锥的底面圆的半径为（　　）
A．π B．3 C．2 D．1


4．如图，AB是⊙O的直径，CD是弦（点C不与点A，点B重合，且点C与点D位于直径AB两侧），若∠AOD＝110°，则∠BCD等于（　　）

A．25° B．35° C．55° D．70°
5．如图，⊙O是正五边形ABCDE的外接圆．若⊙O的半径为5，则半径OA，OB与围成的扇形的面积是（　　）

A．2π B．5π C． D．10π
6．半径为2cm，圆心角为90°的扇形的面积等于（　　）
A．1cm2 B．πcm2 C．2πcm2 D．4πcm2
7．如图，AB是⊙O的直径，C，D是⊙O上两点，若∠D＝55°，则∠BOC的度数是（　　）

A．35° B．55° C．60° D．70°


8．如图，AB是⊙O的直径，PA与⊙O相切于点A，BC∥OP交⊙O于点C．若∠B＝70°，则∠OPC的度数为（　　）

A．10° B．20° C．30° D．40°
9．如图，点A，B，C在⊙O上，∠AOB＝100°，∠OBC＝20°，则∠OAC的度数为（　　）

A．20° B．25° C．30° D．40°
二．填空题（共11小题）
10．如图，在⊙O中，＝，AB＝8，半径r＝5，则DC＝　 　．

11．如图，△ABC内接于⊙O，∠ACB＝50°，则∠ABO＝　 　°．





12．如图所示的正方形网格中，O，A，B，C，D是网格线交点，若与所在圆的圆心都为点O，则与的长度之比为　 　．

13．如图，已知A，B，C是⊙O上三点，∠C＝20°，则∠AOB的度数为　 　．

14．数学课上，李老师提出如下问题：
已知：如图，AB是⊙O的直径，射线AC交⊙O于C．
求作：弧BC的中点D．
同学们分享了四种方案：
①如图1，连接BC，作BC的垂直平分线，交⊙O于点D．
②如图2，过点O作AC的平行线，交⊙O于点D．
③如图3，作∠BAC的平分线，交⊙O于点D．
④如图4，在射线AC上截取AE，使AE＝AB，连接BE，交⊙O于点D．

上述四种方案中，正确的方案的序号是 　 　．



15．如图，在⊙O中，半径OC⊥AB于点H，若∠OAB＝40°，则∠ABC＝　 　°．

16．如图，AB是⊙O的弦，C是⊙O上的一点，且∠ACB＝60°，OD⊥AB于点E，交⊙O于点D．若⊙O的半径为6，则弦AB的长为　 　．

17．如图，⊙O是△ABC的外接圆，半径是2，∠BAC＝60°，则的长是　 　．

18．如图所示的网格是正方形网格，O，A，B，C是网格线交点，⊙O恰好经过点A，B，C，OD为与网格线重合的一条半径，则∠ABC与∠AOD大小关系为：∠ABC　 　∠AOD（填“＞”，“＝”或“＜”）．

19．若两圆的半径分别是1和3，且两圆的位置关系是相切，则圆心距为　 　．


20．如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，连结OC，若OC＝5，AE＝2，则CD＝　 　．

三．解答题（共36小题）
21．如图，AB是⊙O的弦，C为⊙O上一点，过点C作AB的垂线与AB的延长线交于点D，连接BO并延长，与⊙O交于点E，连接EC，∠ABE＝2∠E．
（1）求证：CD是⊙O的切线；
（2）若tanE＝，BD＝1，求AB的长．

22．如图，AB是⊙O的直径，C是⊙O上一点，D是OB中点，过点D作AB的垂线交AC的延长线于点F，FD上有一点E，CE＝EF．
（1）求证：CE是⊙O的切线；
（2）如果sinF＝，EF＝1，求AB的长．


23．如图，△ABC是⊙O的内接三角形，过点C作⊙O的切线交AB的延长线于点D，OE⊥BC于点E，交CD于点F．
（1）求证：∠A+∠OFC＝90°；
（2）若tanA＝，BC＝6，求线段CF的长．

24．如图，PA与⊙O相切于点A，点B在⊙O上，PA＝PB．
（1）求证：PB是⊙O的切线；
（2）AD为⊙O的直径，AD＝2，PO与⊙O相交于点C，若C为PO的中点，求PD的长．












25．已知：如图，△ABC中，AB＝AC，AB＞BC．
求作：线段BD，使得点D在线段AC上，且∠CBD＝∠BAC．
作法：①以点A为圆心，AB长为半径画圆；
②以点C为圆心，BC长为半径画弧，交⊙A于点P（不与点B重合）；
③连接BP交AC于点D．
线段BD就是所求作的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接PC．
∵AB＝AC，
∴点C在⊙A上．
∵点P在⊙A上，
∴∠CPB＝∠BAC　 　（填推理的依据）．
∵BC＝PC，
∴∠CBD＝　 　．
∴∠CBD＝∠BAC










26．如图，△ABC中，∠C＝90°，点E在AB上，以BE为直径的⊙O与AC相切于点D，与BC相交于点F，连接BD，DE．
（1）求证：∠ADE＝∠DBE；
（2）若sinA＝，BC＝6，求⊙O的半径．

27．如图，AB是⊙O的直径，AC是⊙O的弦，点D平分劣弧，连接BD，过点D作AC的垂线EF，交AC的延长线于点E，交AB的延长线于点F．
（1）依题意补全图形；
（2）求证：直线EF是⊙O的切线；
（3）若AB＝5，BD＝3，求线段BF的长．









28．如图，AB为⊙O的弦，C为AB的中点，D为OC延长线上一点，DA与⊙O相切，切点为A，连接BO并延长，交⊙O于点E，交直线DA于点F．
（1）求证：∠B＝∠D；
（2）若AF＝4，sinB＝，求⊙O的半径．

29．如图，AB为⊙O直径，点C，D在⊙O上，且＝，过点C作CE∥BD，交AB延长线于点E．
（1）求证：CE为⊙O切线；
（2）过点C作CF⊥AE交BD于H点，∠E＝30°，CH＝6，求BE的长．













30．已知：如图，射线AP．
求作：△ABC，使得点B在射线AP上，∠C＝90°，∠A＝60°．
作法：①在射线AP上任取一点M；
②以点M为圆心，MA的长为半径画圆，交射线AP于另一点B；
③以点A为圆心，AM的长为半径画弧，在射线AP的上方交⊙M于点C；
④连接AC、BC．
所以△ABC为所求作的三角形．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∵AB为⊙M的直径，点C在⊙M上，
∴∠ACB＝90°（　 　）（填推理依据）．
连接MC．
∵MA＝MC＝AC，
∴△AMC为等边三角形（　 　）（填推理依据）．
∴∠A＝60°．

31．如图，AB是⊙O的直径，弦CD⊥AB于点E，⊙O的切线CF交AB的延长线于点F，连接OC，DF．
（1）求证：DF是⊙O的切线；
（2）若sin∠OFC＝，BF＝10，求CD的长．





32．如图，⊙O是△ABC的外接圆，圆心O在AC上．过点B作直线交AC的延长线于点D，使得∠CBD＝∠CAB．过点A作AE⊥BD于点E，交⊙O于点F．
（1）求证：BD是⊙O的切线；
（2）若AF＝4，，求BE的长．

33．下面是小华设计的“作∠AOB的角平分线”的尺规作图过程，请帮助小华完成尺规作图并填空（保留作图痕迹）．
步骤
作法
推断
第一步
在OB上任取一点C，以点C为圆心，OC为半径作半圆，分别交射线OA，OB于点P，点Q，连接PQ
∠OPQ＝　 　

°，理由是
　 　
第二步
过点C作PQ的垂线，交PQ于点D，交于点E
PD＝DQ，＝
　 　
第三步
作射线OE
射线OE平分∠AOB
射线OE为所求作



34．如图，在Rt△ABC中，∠C＝90°，点O在AC上，∠OBC＝∠A，点D在AB上，以点O为圆心，OD为半径作圆，交DO的延长线于点E，交AC于点F，∠E＝∠BOC．
（1）求证：AB为⊙O的切线；
（2）若⊙O的半径为3，tan∠OBC＝，求BD的长．

35．下面是小景设计的“过直线外一点作这条直线的垂线”的尺规作图过程．
已知：如图1，直线l和l外一点A．
求作：直线AE，使得AE⊥l于点E．
作法：①在直线l上取一点B，连接AB（如图2）；
②作线段AB的垂直平分线CD，交AB于点O；
③以O为圆心，OB长为半径作圆，交直线l于点E；
④作直线AE．
所以直线AE即为所求作的直线．

（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∵CD为线段AB的垂直平分线，
∴OA＝　 　．
∴AB＝2OB．
∴AB是⊙O的直径．
∴∠AEB＝90°（　 　）（填推理的依据）．
∴AE⊥l．
36．如图，OA是⊙O的半径，AB与⊙相切于点A，点C在⊙O上且AC＝AB，D为AC的中点，连接OD，连接CB交OD于点E，交OA于点F．
（1）求证：OE＝OF；
（2）若OE＝3，sin∠AOD＝，求BF的长．

37．如图，AB为⊙O的直径，点C，点D在⊙O上，且点C是的中点，DE是⊙O的切线且DE⊥AC交AC的延长线于点E，连接OC．
（1）求证：△AOC是等边三角形；
（2）若DE＝2，求AC的长．







38．下面是小于同学设计的“过直线外一点作这条直线的平行线”的尺规作图过程．
已知：直线l及直线l外一点P．
求作：直线PQ，使得PQ∥l．
小于同学的作法：如下，
（1）在直线l的下方取一点O；
（2）以点O为圆心，OP长为半径画圆，⊙O交直线l于点C，D（点C在左侧），连接CP；
（3）以点D为圆心，CP长为半径画圆，交⊙O于点Q，N（点Q与点P位于直线l同侧）；
（4）作直线PQ；
所以直线PQ即为所求．
请你依据小于同学设计的尺规作图过程，完成下列问题．
（1）使用直尺和圆规，完成作图；（保留作图痕迹）
（2）完成下面的证明：
证明：连接DP
∵CP＝DQ
∴＝　 　（填推理的依据）．
∴∠PDC＝∠DPQ　 　（填推理的依据）．
∴PQ∥l　 　（填推理的依据）．









39．已知，如图，点A，C，D在⊙O上，且满足∠C＝45°．连接OD，AD，过点A作直线AB∥OD，交CD的延长线于点B．
（1）求证：AB是⊙O的切线；
（2）如果OD＝CD＝2，求AC边的长．

40．已知：∠MAN，B为射线AN上一点．
求作：△ABC，使得点C在射线AM上，且∠ABC＝∠CAB．
作法：①以点A为圆心，AB长为半径画弧，交射线AM于点D，交射线AN的反向延长线于点E；
②以点E为圆心，BD长为半径画弧，交于点F；
③连接FB，交射线AM于点C．
△ABC就是所求作的三角形．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明：
证明：连接BD，EF，AF，
∵点B，E，F在⊙A上，
∴∠EBF＝∠EAF（ 　 　）（填写推理的依据）．
∵在⊙A中，BD＝EF，
∴∠DAB＝　 　．
∴∠ABC＝∠CAB．




41．如图，AB为⊙O的直径，点C在AB的延长线上，CD与⊙O相切于D，过点B作BE∥CD交⊙O于点E，连接AD，AE，∠EAD＝22.5°．
（1）求∠EAB的度数；
（2）若BC＝2，求BE的长．

42．已知：在△ABC中，AB＝AC，AD是边BC上的中线．
求作：∠BPC，使∠BPC＝∠BAC．
作法：
①作线段AB的垂直平分线MN，与直线AD交于点O；
②以点O为圆心，OA长为半径作⊙O；
③在上取一点P（不与点A重合），连接BP，CP．
∠BPC就是所求作的角．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接OB，OC．
∵MN是线段AB的垂直平分线，
∴OA＝　 　．
∵AB＝AC，AD是边BC上的中线，
∴AD⊥BC．
∴OB＝OC．
∴⊙O为△ABC的外接圆．
∵点P在⊙O上，
∴∠BPC＝∠BAC（　 　）（填推理的依据）．



43．如图，AB为⊙O的直径，点C在⊙O上，过点C作⊙O的切线CM，过点A作AD⊥CM于点D，交BC的延长线于点E．
（1）求证：AE＝AB；
（2）若AB＝10，cosE＝，求CD的长．

44．如图，AD是⊙O的直径，P是⊙O外一点，连接PO交⊙O于点C，PB，PD分别切⊙O于点B，D，连接AB，AC．
（1）求证：AB∥OP；
（2）连接PA，若PA＝2，tan∠BAD＝2，求PC长．









45．如图，AB为⊙O的直径，C为⊙O上一点，过点C作⊙O的切线CE，过点B作BD⊥CE于点D．
（1）求证：∠ABC＝∠DBC；
（2）若CD＝6，sin∠ABC＝，求AB的长．

46．已知：如图，∠MAN＝α（0°＜α＜45°）．
求作：△ABC，使得∠ABC＝2∠BAC，
作法：①在射线AN上取点O，以点O为圆心，OA长为半径画圆，交射线AM于点C；
②连接CO；
③以点C为圆心，CO长为半径画弧，交射线AN于点B；连接CB，△ABC就是所求作．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明
证明：
∵点C、A在⊙O上．
∴∠COB＝2∠CAB（　 　）（填推理依据）．
∵CB＝CO，
∴∠CBA＝　 　．
∴∠CBA＝2∠CAB．


47．如图，点E是⊙O中弦AB的中点，过点E作⊙O的直径CD，P是⊙O上一点，过点P作⊙O的切线，与AB的延长线交于F，与CD的延长线交于点G，连接CP与AB交于点M．
（1）求证：FM＝FP；
（2）若点P是FG的中点，cos∠F＝，⊙O半径长为3，求EM长．

48．如图，DE是⊙O的直径，CA为⊙O的切线，切点为C，交DE的延长线于点A，点F是⊙O上的一点，且点C是弧EF的中点，连接DF并延长交AC的延长线于点B．
（1）求证：∠ABD＝90°；
（2）若BD＝3，tan∠DAB＝，求⊙O的半径．










49．下面是小融设计的“过直线外一点作圆与这条直线相切”的尺规作图过程．
已知：直线l及直线l外一点P（如图1）．
求作：⊙P，使它与直线l相切．
作法：如图2，
①在直线l上任取两点A，B；
②分别以点A，点B为圆心，AP，BP的长
为半径画弧，两弧交于点Q；
③作直线PQ，交直线l于点C；
④以点P为圆心，PC的长为半径画⊙P．
所以⊙P即为所求．
根据小融设计的尺规作图过程，
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接AP，AQ，BP，BQ．
∵AP＝　 　，BP＝　 　，
∴点A，点B在线段PQ的垂直平分线上．
∴直线AB是线段PQ的垂直平分线．
∵PQ⊥l，PC是⊙P的半径，
∴⊙P与直线l相切（　 　）（填推理的依据）．




50．如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，过点A作⊙O的切线交直线OD于点P，连接PC．
（1）求证：∠PCA＝∠ABC；
（2）若BC＝4，tan∠APO＝，求PA的长．

51．如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．
（1）求证：∠FEB＝∠ECF；
（2）若AB＝6，sin∠CEB＝，求CB和EF的长．











52．已知：如图，锐角△ABC．
求作：在AB上取点D，AC上取点E，使得△AED∽△ABC，
作法：①分别以点B和点C为圆心，大于长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点O；
②以点O为圆心，OB长为半径画圆，在BC上方交AB于点D，交AC于点E；
③连接DE，△AED即为所求作．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：
∵点B、C、E、D均在⊙O上．
∴∠B+∠DEC＝180°（　 　）（填推理依据）．
∵∠AED+∠DEC＝180°，
∴∠AED＝　 　．
∵∠A＝∠A，
∴△AED∽△ABC．








53．如图，AB是⊙O直径，点C是⊙O上一点，过点C作⊙O的切线CG，过点B作CG的垂线，垂足为点D，交⊙O于点E，连接CB．
（1）求证：CB平分∠ABD；
（2）若，BC＝5，求CE长．

54．已知，如图，在△ABC中，D是AB边上一点，⊙O过D、B、C三点，直线AC是⊙O的切线，OD∥AC．
（1）求∠ACD的度数；
（2）如果∠ACB＝75°，⊙O的半径为2，求BD的长．










55．如图，在△ABC中，AB＝BC，以AB为直径作⊙O，交AC于点D，过点D作BC的垂线，垂足为点E，与AB的延长线交于点F．
（1）求证：DF为⊙O的切线；
（2）若⊙O的直径为5，tanC＝，求EF的长．

56．如图，AB为⊙O的直径，DE为⊙O的切线，点D是AC中点．
（1）求证：DE⊥BC；
（2）如果DE＝2，tanC＝，求⊙O的半径．