人教A版（2019）必修二 高中数学 期中必考点09 立体几何综合 （学生版+解析版）练习题

这是一份人教A版（2019）必修二 高中数学 期中必考点09 立体几何综合 （学生版+解析版）练习题，文件包含人教A版2019必修二高中数学必考点09立体几何综合解析版docx、人教A版2019必修二高中数学必考点09立体几何综合原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
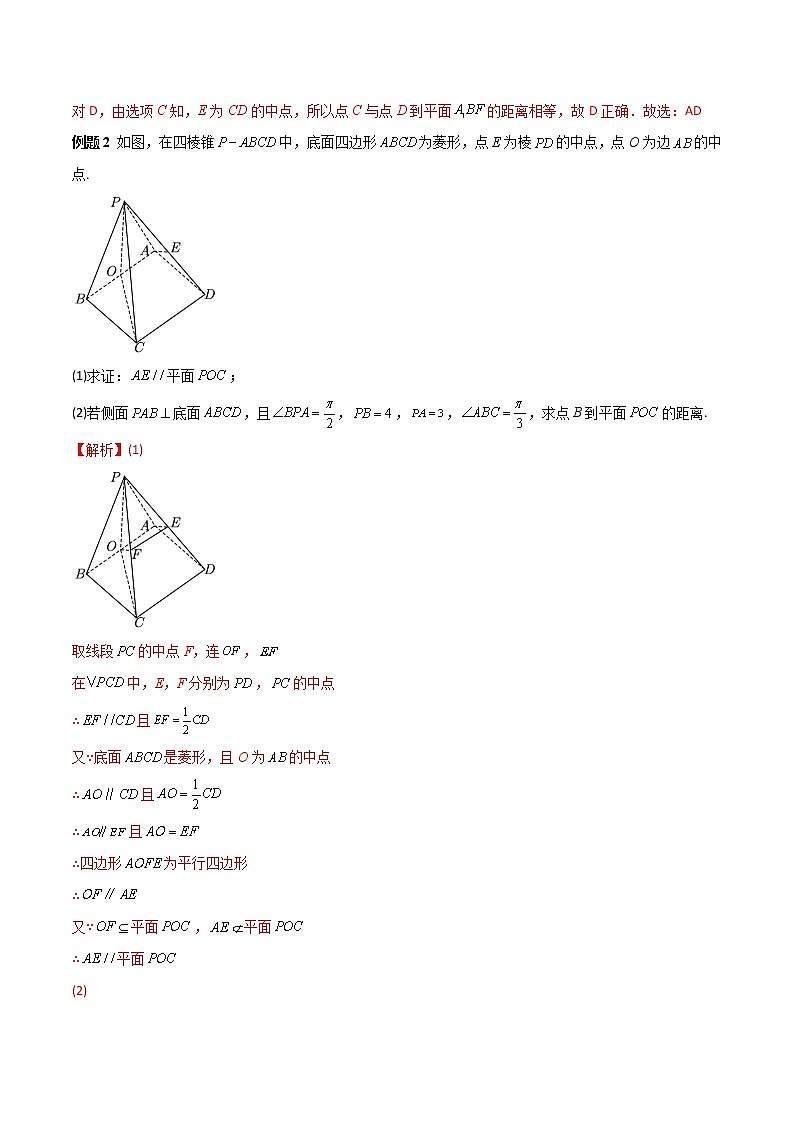
必考点09  立体几何综合 题型一  空间几何体的距离问题例题11．如图，正方体的棱长为2，F为的中点．则（       ）A．B．直线AD与BF所成角的正切值为C．平面截正方体所得的截面面积为4D．点C与点D到平面的距离相等 例题2 如图，在四棱锥中，底面四边形为菱形，点E为棱的中点，点O为边的中点.(1)求证：平面；(2)若侧面底面，且，，，，求点B到平面的距离.【解题技巧提炼】空间几何体的距离问题        解决空间中的距离问题，常用几何法，其中等体积法作为求高，即点到平面的距离是一种常见方法，其次可以利用构造，投影，直角三角形等解三角形，解决长度问题题型二  空间几何体的角度问题例题1如图，在三棱锥P－ABC中，PA⊥AB，PA⊥AC，AB⊥BC，，D为线段AC的中点，E为线段PC上一点.(1)求证：平面BDE⊥平面PAC；(2)求二面角P－BC－A的平面角的大小. 例题2已知正方体.(1)证明：平面；(2)求异面直线与BD所成的角. 【解题技巧提炼】        空间中的角分为线线角、线面角和面面角，其中线线角可以将直线平移到同一个平面内，利用正余弦定理解三角形求夹角，线面角需要将直线投影到平面上，则直线与直线投影所成的夹角就是线面角，常利用直角三角形处理，面面角（二面角）是往交线上作垂线，则两垂线之间的夹角就是二面角。 题型一  空间几何体的距离问题1．已知三棱锥三条侧棱、、两两互相垂直，且，、分别为该三棱锥的内切球和外接球上的动点，则、两点间距离的最小值为______.2．如图，三棱柱中，侧面为菱形，，且.(1)证明：；(2)若，，，求点到平面的距离.题型二  空间几何体的夹角问题1．如图，在四棱锥中，底面为平行四边形，平面，平面平面，，，为的中点．(1)求证：；(2)求二面角的正切值．【解析】(1)证明：过在平面内作，垂足为点，平面平面，平面平面，平面，平面，平面，则，平面，平面，，，平面，平面，.(2)解：过点在平面内作，垂足为点，连接，由（1）知平面，平面，，，，所以，平面，因为平面，所以，，所以，为二面角的平面角，平面，平面，，，，则，为的中点，所以，，由，，因此，二面角的正切值为.1．如图1，在等腰梯形中，，，，．将与分别沿，折起，使得点、重合（记为点），形成图2，且是等腰直角三角形．(1)证明：平面平面；(2)求二面角的正弦值；(3)若，求四棱锥的体积．一、解答题1．多面体ABCDE中，与均为边长为2的等边三角形，为腰长为的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD，F为BC的中点.(1)求证：平面ECD；(2)求多面体ABCDE的体积.2．如图，在棱长为2的正方体中，E，F，G，H分别是所在棱的中点．(1)求证：E，F，G，H四点共面；(2)求三棱锥的体积．3．在如图所示的几何体中，平面平面ABCD，M四边形ADNM是矩形，四边形ABCD为梯形，，，．(1)求证：平面MBC；(2)已知直线AN与BC所成角为60°，求点C到平面MBD的距离4．如图，四棱锥S-ABCD的底面是长方形，SA⊥底面ABCD，3CE=CD，SC⊥BE.(1)证明：平面SBE⊥平面SAC；(2)若，AD=1，求CD及三棱锥C-SBE的体积..5．如图，在四棱锥中，四边形为矩形，平面平面，F为棱的中点，P为棱上一点．(1)求证：平面；(2)当P到平面的距离为时，求线段的长．6．如图，是边长为的等边三角形，分别在边上，且，为边的中点，交于点，沿将折到的位置，使.(1)证明：平面；(2)若平面内的直线平面，且与边交于点，是线段的中点，求三棱锥的体积.7．如图，三棱锥的底面为直角三角形，为斜边的中点，顶点在底面的投影为，，，.(1)求的长；(2)求异面直线与所成角的余弦值.8．如图，在多面体中，为等边三角形，，，，，F为EB的中点.(1)证明：平面；(2)求多面体的体积.