2022年重庆市中考数学第2轮专题复习一次函数和反函数训练1

这是一份2022年重庆市中考数学第2轮专题复习一次函数和反函数训练1，共8页。
一次函数和反函数训练1
如图，在平面直角坐标系xOy中，点A（3，2）在反比例函数y=kx（x＞0）的图象上，点B在OA的延长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AC，AD．
（1）求该反比例函数的解析式；
（2）若S△ACD=32，设点C的坐标为（a，0），求线段BD的长．
如图，一次函数y1=x+2的图象与反比例函数y2=kx（k≠0）的图象交于A、B两点，且点A的坐标为（1，m）．
（1）求反比例函数的表达式及点B的坐标；
（2）根据图象直接写出当y1＞y2时x的取值范围．
如图，一次函数y=kx+b的图象与反比例函数y=mx的图象交于A（-2，1），B（1，n）两点．
（1）求一次函数与反比例函数的表达式；
（2）求△AOB的面积；
（3）根据所给条件，请直接写出不等式kx+b＜mx的解集．
如图，已知直线y=12x与双曲线y=nx交于A，B两点，且点A的横坐标为4．
（1）求k的值；
（2）直接写出不等式nx＞12x的解集．
（3）过原点O的另一条直线l交双曲线y=nx于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．
如图，直线y=mx+6与反比例函数y=kx（x＞0）的图象交于点A（17−32，n）与x轴交于点B（-3，0），M为该图象上任意一点，过M点作x轴的平行线交y轴于点P，交AB于点N．
（1）求m、n的值和反比例函数的表达式；
（2）若点P为MN中点时，求△AMN的面积．
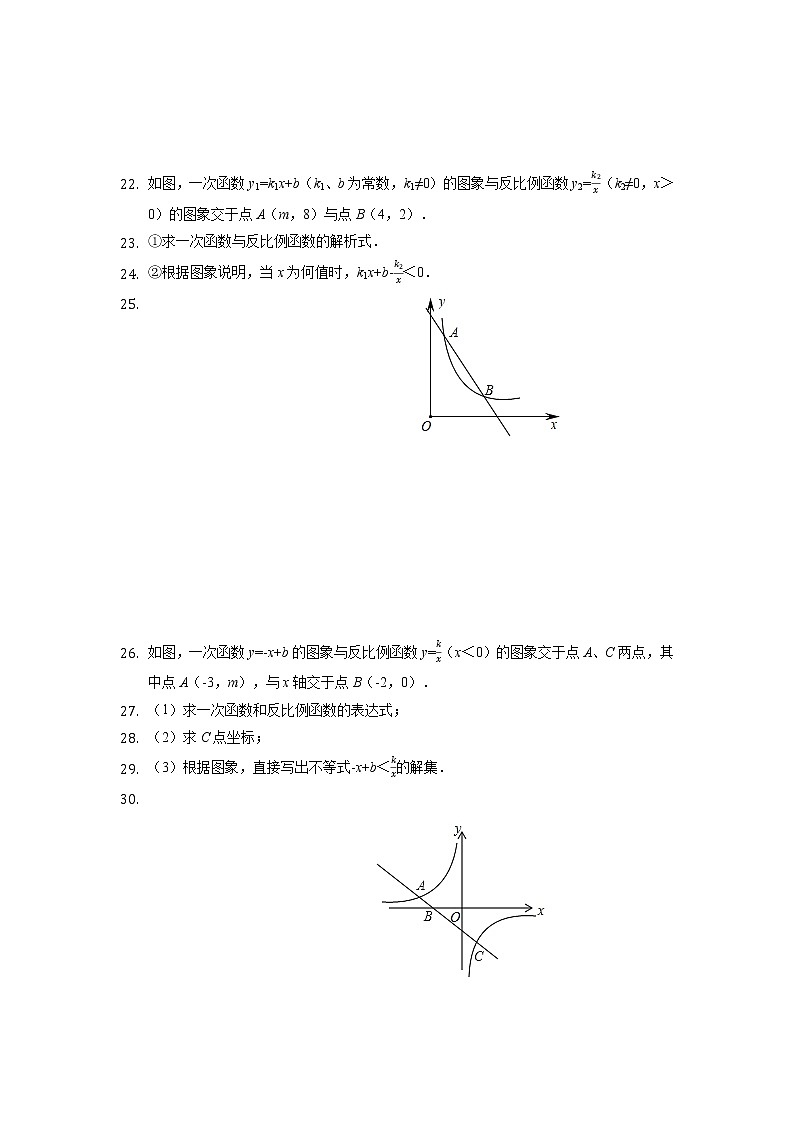
如图，一次函数y1=k1x+b（k1、b为常数，k1≠0）的图象与反比例函数y2=k2x（k2≠0，x＞0）的图象交于点A（m，8）与点B（4，2）．
①求一次函数与反比例函数的解析式．
②根据图象说明，当x为何值时，k1x+b-k2x＜0．
如图，一次函数y=-x+b的图象与反比例函数y=kx（x＜0）的图象交于点A、C两点，其中点A（-3，m），与x轴交于点B（-2，0）．
（1）求一次函数和反比例函数的表达式；
（2）求C点坐标；
（3）根据图象，直接写出不等式-x+b＜kx的解集．
如图，已知一次函数y1=ax+b（a≠0）与反比例函数y2=kx（k＞0），两函数图象交于（4，1），（-2，n）两点．
（1）求a，k的值；
（2）若y2＞y1＞0，求x的取值范围．
如图，直线y=ax（a＞0）与双曲线y=kx（k＞0）交于A、B两点，且点A的坐标为（4，2），点B的坐标为（n，-2）．
（1）求a，n的值；
（2）若双曲线y=y=kx（k＞0）的上点C的纵坐标为8，求△AOC的面积．
如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于B、A两点，与反比例函数y=kx的图象交于点C，连接CO，过C作CD⊥x轴于D，直线AB的解析式为y=-12x+2，CD=3．
（1）求tan∠ABO的值和反比例函数的解析式；
（2）根据图象直接写0＜-12x+2＜kx的自变量x的范围．
如图，一次函数y1=ax+b的图象和反比例函数y2=kx的图象相交于A（2，3）和B（m，-1）两点．
（1）试确定一次函数与反比例函数表达式；
（2）求△OAB的面积；
（3）结合图象，直接写出使y1＞y2成立的x的取值范围．
如图,一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A(-1,n)、B(2,-1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)请直接写出不等式kx+b>mx的解集;
如图所示，在平面直角坐标系中，等腰Rt△OAB的一条直角边OA在x轴的正半轴上，点B在双曲线y=kx（k≠0）上，且∠BAO=90°，S△AOB=2．
（1）求k的值及点A的坐标；
（2）△OAB沿直线OB平移，当点A恰好在双曲线上时，求平移后点A的对应点A'的坐标．
如图，一次函数y=kx+b（k≠0）经过点B（0，1），且与反比例函数y=mx（m≠0）的图象在第一象限有公共点A（1，2）．
（1）求一次函数与反比例函数的解析式；
（2）根据图象写出当x取何值时，一次函数的值小于反比例函数的值？
如图，已知一次函数y1=k1x+b（k1≠0）与反比例函数y2=k2x（k2≠0）的图象交于A（4，1），B（n，-2）两点．
（1）求一次函数与反比例函数的解析式；
（2）请根据图象直接写出y1＜y2时x的取值范围．
如图,一次函数y1=x+2的图象与反比例函数y2=kx(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.