专题11 二次函数-备战2022年中考数学母题题源解密（广东专用）（原卷版）

这是一份专题11 二次函数-备战2022年中考数学母题题源解密（广东专用）（原卷版），共14页。
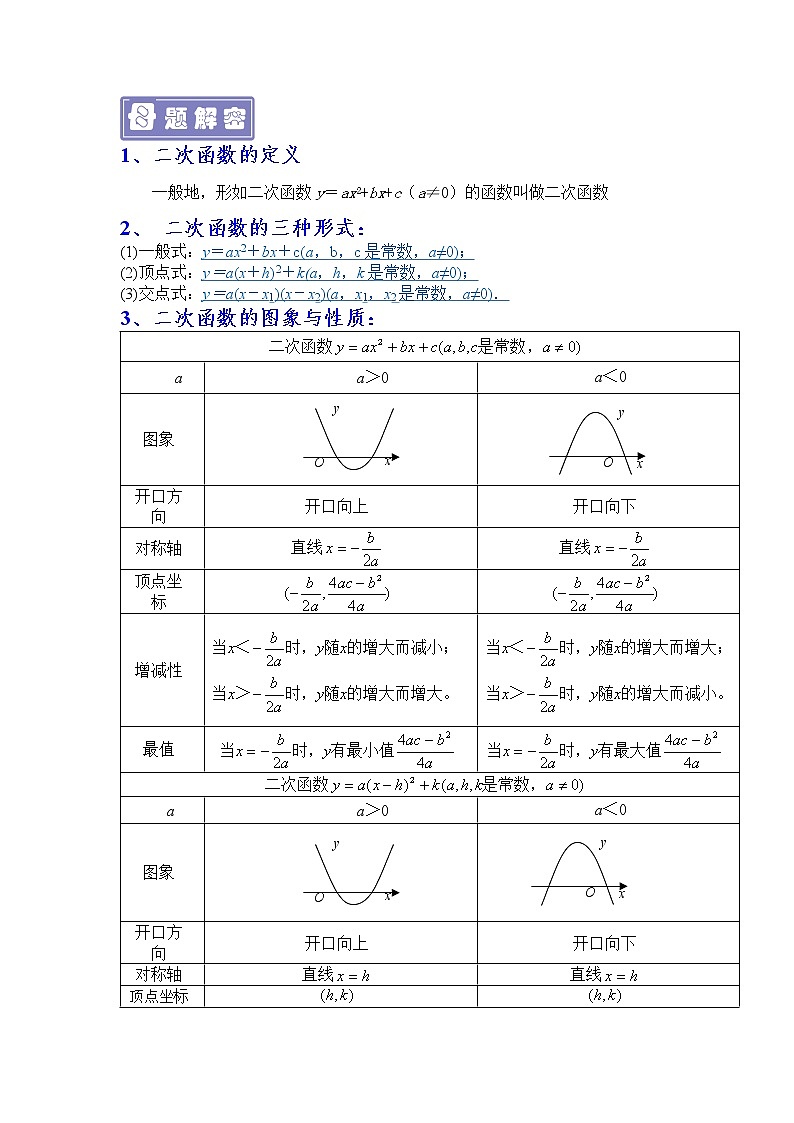
专题11 二次函数【母题来源】2021年中考广东广州卷【母题题文1】（2021·广东广州·中考真题）抛物线经过点、，且与y轴交于点，则当时，y的值为（    ）A． B． C． D．5【母题来源】2021年中考广东卷【母题题文2】（2021·广东·中考真题）设O为坐标原点，点A、B为抛物线上的两个动点，且．连接点A、B，过O作于点C，则点C到y轴距离的最大值（    ）A． B． C． D．1【母题来源】2021年中考广东深圳卷【母题题文3】（2021·广东深圳·中考真题）二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是（    ）A．                  B．C． D．【母题来源】2021年中考广东卷【母题题文4】（2021·广东·中考真题）若一元二次方程（b，c为常数）的两根满足，则符合条件的一个方程为________．【母题来源】2021年中考广东卷【母题题文5】（2021·广东·中考真题）把抛物线向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为______．【母题题文6】（2021·广东·中考真题）我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a，b，c，记，则其面积．这个公式也被称为海伦-秦九韶公式．若，则此三角形面积的最大值为（    ）A． B．4 C． D．5【母题来源】2021年中考广东卷【母题题文7】（2021·广东·中考真题）端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同．在销售中，该商家发现猪肉粽每盒售价50元时，每天可售出100盒；每盒售价提高1元时，每天少售出2盒．（1）求猪肉粽和豆沙粽每盒的进价；（2）设猪肉粽每盒售价x元表示该商家每天销售猪肉粽的利润（单位：元），求y关于x的函数解析式并求最大利润．【母题来源】2021年中考广东深圳卷【母题题文8】（2021·广东深圳·中考真题）某科技公司销售高新科技产品，该产品成本为8万元，销售单价x（万元）与销售量y（件）的关系如下表所示：x（万元）10121416y（件）40302010（1）求y与x的函数关系式；（2）当销售单价为多少时，有最大利润，最大利润为多少？【母题来源】2021年中考广东广州卷【母题题文9】（2021·广东广州·中考真题）已知抛物线（1）当时，请判断点（2，4）是否在该抛物线上；（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；（3）已知点、，若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．1、二次函数的定义一般地，形如二次函数y＝ax2+bx+c（a≠0）的函数叫做二次函数2、 二次函数的三种形式：(1)一般式：y＝ax2＋bx＋c(a，b，c是常数，a≠0)；(2)顶点式：y＝a(x＋h)2＋k(a，h，k是常数，a≠0)；(3)交点式：y＝a(x－x1)(x－x2)(a，x1，x2是常数，a≠0)．          3、二次函数的图象与性质：二次函数aa＞0a＜0图象  开口方向开口向上开口向下对称轴直线直线顶点坐标增减性最值二次函数aa＞0a＜0图象  开口方向开口向上开口向下对称轴直线直线顶点坐标增减性最值3. 二次函数图象的特征与a，b，c及的符号之间的关系：项目字母字母的符号图象的特征aa＞0开口         .a＜0开口         bb=0对称轴为       .ab＞0(b与a同号)对称轴在y轴       侧ab＜0(b与a异号)对称轴在y轴       侧cc=0经过原点（0 ，0）c＞0与y轴        相交c＜0与y轴        相交=0      与x轴有     交点（顶点）＞0与x轴有     交点＜0与x轴有     交点 4.二次函数图象的平移：抛物线与中a相同，则图象的形状和大小都相同，只是位置不同，它们之间可以通过适当的平移得到.具体平移方法如下图所示：（口诀“上加下减，左加右减”）                                                                                   5.二次函数关系式的确定(1)若已知条件是图像上的三个点的坐标，则设一般式y＝ax2＋bx＋c   (a≠0)，将已知三点坐标代入，求出其a，b，c的值．(2)若已知二次函数顶点坐标或对称轴方程与最大（小）值，则设顶点式y＝a(x＋h)2＋k   (a≠0)，将已知条件代入，求出a，h 或k的值．(3)若已知二次函数图像与x轴的两个交点坐标为（x1，0），（x2，0）则设交点式y＝a(x－x1)(x－x2)(a≠0) 将第三点坐标或其他已知条件代入，求出待定系数a，最后将关系式化为一般式．                                                   一、单选题1．下列函数解析式中，一定为二次函数的是（     ）A． y=3x-1 B．y=ax2+bx+c C．s=2t2-2t+1 D．y=x2+ 2．（2019·浙江新昌·中考模拟）将抛物线先向右平移个单位长度，再向下平移个单位长度，平移后所得抛物线解析式为（    ）A． B．C． D．3．已知函数y＝kx2﹣7x﹣7的图象和x轴有交点，则k的取值范围是（　　）A． B． C．且k≠0 D．且k≠04．关于抛物线，下列说法错误的是（    ）A．该抛物线经过原点B．该抛物线的对称轴是直线C．该抛物线的最大值为1D．当时，随增大而减小5．若二次函数y＝ax2+2ax+3a的图象过不同的三个点A(n，y1)，B(1﹣n，y2)，C(﹣1，y3)，且y1＞y2＞y3，则n的取值范围是（　　）A．n＜ B．n＜ C．n＞且n≠2 D．n＞6．（2021·四川中江·一模）二次函数y＝ax2+bx+c（a≠0）与一次函数y＝ax+c在同一坐标系中的图象大致为（　　）A．  B．C．   D．7．二次函数y＝ax2＋bx＋c的图象过点（﹣1，0），对称轴为直线x＝2，若a＞0，则下列结论错误的是（    ）A．当x＞2时，y随着x的增大而增大  B．（a＋c）2＝b2C．若A（x1，m）、B（x2，m）是抛物线上的两点，当x＝x1＋x2时，y＝cD．若方程a（x＋1）（5﹣x）＝﹣1两根为x1、x2，且x1＜x2，则﹣1＜x1＜5＜x28．（2021·广东·佛山市华英学校一模）二次函数（，，为常数，且中的与的部分对应值如下表：013353下列结论：①该抛物线的开口向下；②该抛物线的顶点坐标为（1，5）；③当时，随的增大而减少；④3是方程的一个根，其中正确的个数为（    ）A．4个 B．3个 C．2个 D．1个9．（2021·辽宁·建昌县教师进修学校二模）如图和都是边长为的等边三角形，它们的边在同一条直线上，点，重合，现将沿着直线向右移动，直至点与重合时停止移动．在此过程中，设点移动的距离为，两个三角形重叠部分的面积为，则随变化的函数图像大致为（  ）A．  B． C．  D． 10．（2021·湖南·长沙市开福区青竹湖湘一外国语学校二模）已知二次函数（h为常数），当自变量x的值满足1≤x≤3时，其对应的函数值y的最小值为1，则h的值为（    ）A．2或4 B．0或4 C．2或3 D．0或3  11．（2021·四川省宜宾市第二中学校一模）二次函数的部分图象如图所示，图象过点，对称轴为直线，下列结论：①；；③；④若点、点、点在该函数图象上，则；⑤若方程的两根为和，且，则；⑥， 其中正确的结论有（ ）A．3 B．4 C．5 D．612．（2020·浙江杭州·模拟预测）若二次函数的图象经过、、、则下列命题正确的是（    ）A．若且，则 B．若且，则C．若且，则 D．若，则  二、填空题13．（2017·河北·模拟预测）已知函数 的图象与 轴有交点，则 的取值范围为______．14．（2020·江苏鼓楼·模拟预测）二次函数的图象开口向下，则m__________．15．（2021·山东·青岛大学附属中学二模）抛物线（为常数）与轴交点的个数是______．16．（2021·内蒙古赛罕·二模）对于二次函数，图象的对称轴为____________，当自变量x满足时，函数值y的取值范围为，则a的取值范围为________．17．（2021·湖南怀化·三模）已知抛物线开口向上且经过点,双曲线经过点．给出下列结论：①；②；③,是关于的一元二次方程的两个实数根．其中正确的结论是________（填写序号）．18．（2021·吉林·长春市解放大路学校模拟预测）在平面直角坐标系中，，为抛物线上任意两点，其中，设抛物线的对称轴为直线，若对于任意，都有，则m的取值范围为________．19．（2021·江苏江都·一模）在平面直角坐标系中，我们把横、纵坐标均为整数的点称为整点．若反比例函数与二次函数的图象在第一象限围成的封闭图形（不包括边界）内有且仅有2个整点，则实数的取值范围为_______．20．（2021·江苏·苏州工业园区星湾学校二模）已知抛物线（为常数，）经过点，点是x轴正半轴上的动点．点在抛物线上，当的最小值为时，b的值为_____．21．（2021·辽宁大连·二模）如图，点A（0，1），平行于x轴的直线AC分别交抛物线与（x≥0）于B、C两点，过点C作y轴的平行线交于点D，直线DE∥AC，交于点E，则DE＝________．22．（2021·广西玉林·一模）已知二次函数的图象与x轴相交于A，B两点，点A在点B的左侧，将此二次函数图象在x轴下方的部分沿着x轴翻折，原图像保持不变，得到一个新的图象．当直线与此图象有且只有四个公共点时，则n的取值范围为________．23．（2021·湖北青山·一模）小明在研究抛物线（为常数）时，得到如下结论：①无论取何实数，的值都小于0；②该抛物线的顶点始终在直线上；③当时，随的增大而增大，则；④该抛物线上有两点，，若，，则．其中一定正确的是______（填序号即可）． 24．（2021·湖北武汉·模拟预测）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a）．下列结论：①abc＜0；②5a﹣b+c＝0；③若方程a（x+5）（x﹣1）＝﹣1有两个根x1和x2，且x1＜x2， 则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|＝1有四个根，则这四个根的和为﹣8．其中正确的结论有_______． 三、解答题25．（2018·广东中山·一模）已知抛物线y＝x2﹣（2m+1）x+m2+m，其中m是常数．（1）求证：不论m为何值，该抛物线与z轴一定有两个公共点；（2）若该抛物线的对称轴为直线x＝，请求出该抛物线的顶点坐标．       26．（2021·广东深圳·一模）某公司销售一种商品，成本为每件20元，经过市场调查发现，该商品的日销售量y（件）与销售单价x（元）是一次函数关系，其销售单价、日销售量的三组对应数值如下表：销售单价x（元）406080日销售量y（件）806040（1）求y与x的关系式；（2）若物价部门规定每件商品的利润率不得超过100%，设日利润为w元，求公司销售该商品获得的最大日利润；（3）若物价部门规定该商品销售单价不能超过a元，并且由于某种原因，该商品每件成本变成了之前的2倍，在日销售量y（件）与销售单价x（元）保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求a的值．   27．（2021·广东·西南中学三模）某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜．某种蔬菜的销售单价与销售月份之间的关系如图（1）所示，每千克成本与销售月份之间的关系如图（2）所示．（其中图（1）的图象是直线，图（2）的图象是抛物线，其最低点坐标是（6，1））．（1）求每千克蔬菜销售单价y与销售月份x之间的关系式；（2）判断哪个月份销售每千克蔬菜的收益最大？并求最大收益；（3）求出一年中销售每千克蔬菜的收益大于1元的月份有哪些？  28．（2021·广东·深圳市宝安中学（集团）模拟预测）某商场销售一种小商品，进货价为40元/件．当售价为60元/件时，每天的销售量为300件．在销售过程中发现：销售单价每上涨2元，每天的销售量就减少20件．设销售价格上涨元/件（为偶数），每天的销售量为件．（1）请写出与的函数关系式_______．（2）若商场每天盈利5760元，则每件涨价多少钱？（3）设每天的销售利润为元，为了让利于顾客，则每件商品的销售单价定为多少元时，每天获得的利润最大，最大利润是多少？      29．（2021·广东光明·三模）某商家经销一种绿茶，用于装修门而已投资3000元，已知绿茶每千克成本50元，在第一个月的试销时间内发现，销量w（）随销售单价x（元/）的变化而变化，满足函数关系式，若该绿茶的月销售利润为y（元）（销售利润=单价×销售量-成本-投资）（1）求y与x之间的函数关系式（不必写出变量x的取值范围）．并求出x为何值时，y的值最大？（2）若在第一个月里，按使y获得最大值的销售单价进行销售后，在第二个月里受物价部门干预，销售单价不得高于90元，要想在全部收回投资的基础上使第二个月的利润达到1700元，那么第二个月里应该确定销售单价为多少元？        30．（2021·广东·广州大学附属中学一模）某超市购进一批时令水果，成本为10 元/千克，根据市场调研发现，这种水果在未来30天的销售单价m(元/千克)与时间x(天)之间的函数关系式为（且为整数），且其日销售量y (千克)与时间x(天)之间的函数关系如图所示：（1）求每天销售这种水果的利润W(元)与x(天)之间的函数关系式；（2）问哪一天销售这种水果的利润最大？最大日销售利润为多少？31．（2020·广东·珠海市第九中学一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＞0）与x轴交于点A(﹣2，0)、B（点A在点B右侧），与y轴交于点C，对称轴为直线x＝2．（1）填空：点B的坐标是__________；（2）连接AC，BC，若△ABC的面积为24，求此抛物线的解析式；（3）在第（2）小题的条件下，点Q为x轴正半轴上一点．连接CQ，将△ACQ绕点Q旋转180°得到△FGQ，点C恰好旋转到点G，连接AG，CF．当△FGQ为直角三角形时，求点Q的坐标．     32．（2019·广东梅州·三模）如图，Rt△ABO的直角边OB在x轴上，OB＝2，AB＝1，将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO，抛物线y＝﹣+bx+c经过A，C两点．（1）求点A，C的坐标；（2）求二次函数的解析式；（3）连接AC，点P是抛物线上一点，直线OP把△AOC的周长分成相等的两部分，求点P的坐标．33．（2021·广东·珠海市九洲中学一模）如图，抛物线经过，两点，与轴交于点，，以为边作矩形，其中边经过抛物线的顶点，点是抛物线上一动点（点不与点，重合），过点作轴的平行线与直线交于点，与直线交于点，连接交直线于点．（1）求该抛物线的解析式以及顶点的坐标；（2）当线段时，求点的坐标；（3）在抛物线上是否存在点，使得以点，，，为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．