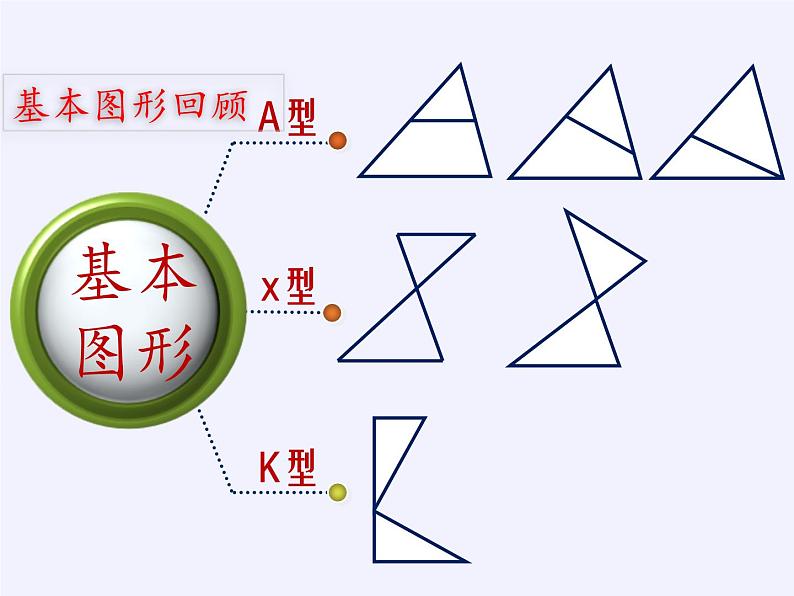
初中数学沪科版九年级上册第22章 相似形22.5 综合与实践 测量与误差图文ppt课件

这是一份初中数学沪科版九年级上册第22章 相似形22.5 综合与实践 测量与误差图文ppt课件，共17页。PPT课件主要包含了基本图形，基本图形回顾，追根溯源，K字型的常见形态，问题1，问题2，小试身手，思考练习，课堂小结等内容，欢迎下载使用。

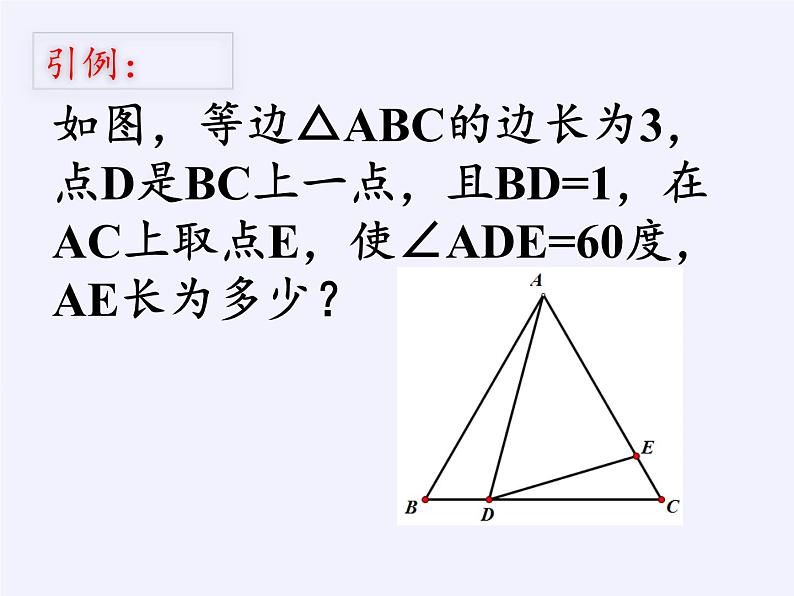
如图，等边△ABC的边长为3，点D是BC上一点，且BD=1，在AC上取点E，使∠ADE=60度，AE长为多少？
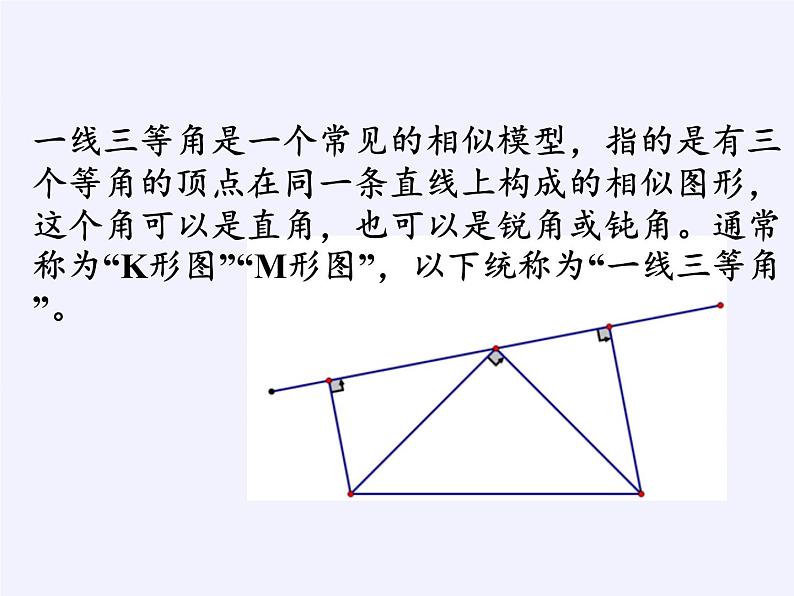
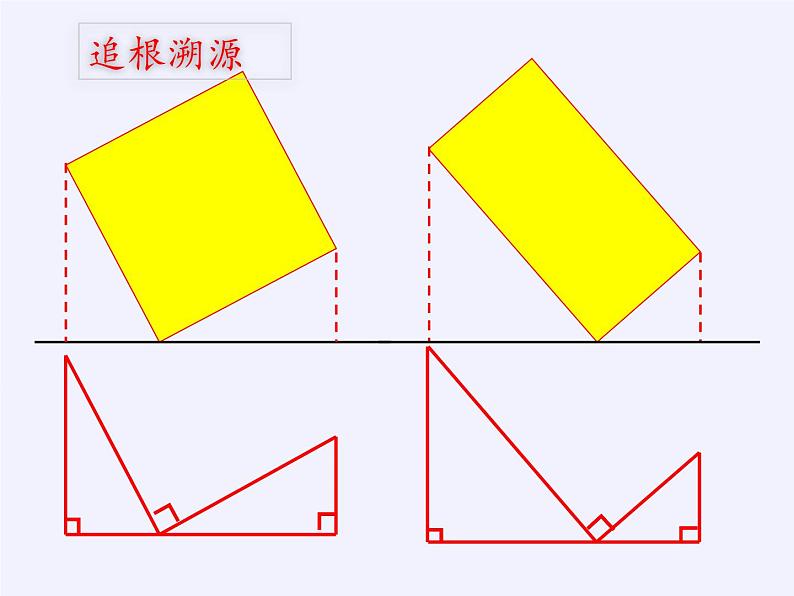
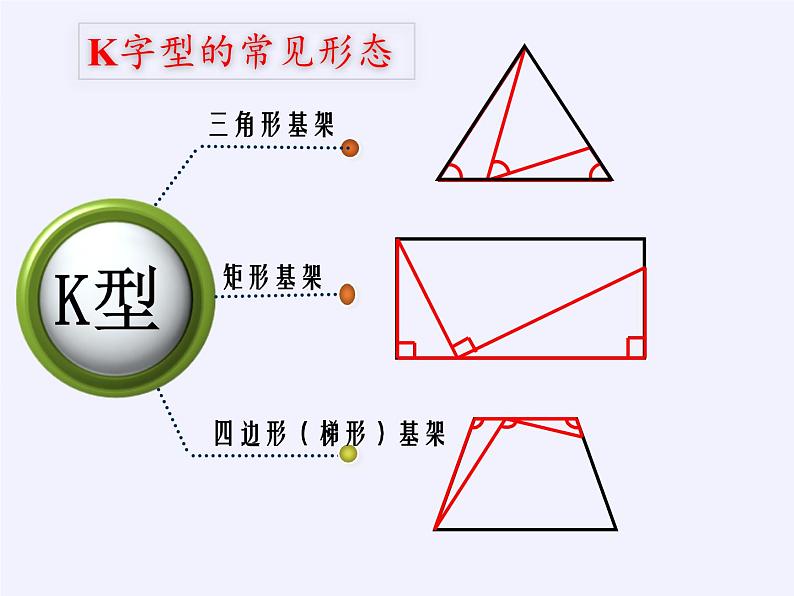
一线三等角是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。通常称为“K形图”“M形图”，以下统称为“一线三等角”。
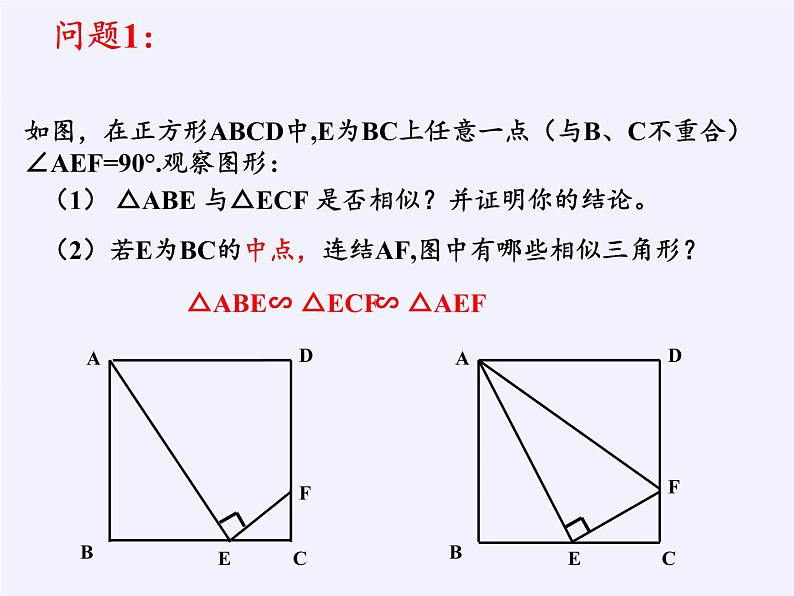
如图，在正方形ABCD中,E为BC上任意一点（与B、C不重合）∠AEF=90°.观察图形：
（2）若E为BC的中点，连结AF,图中有哪些相似三角形？
（1） △ABE 与△ECF 是否相似？并证明你的结论。
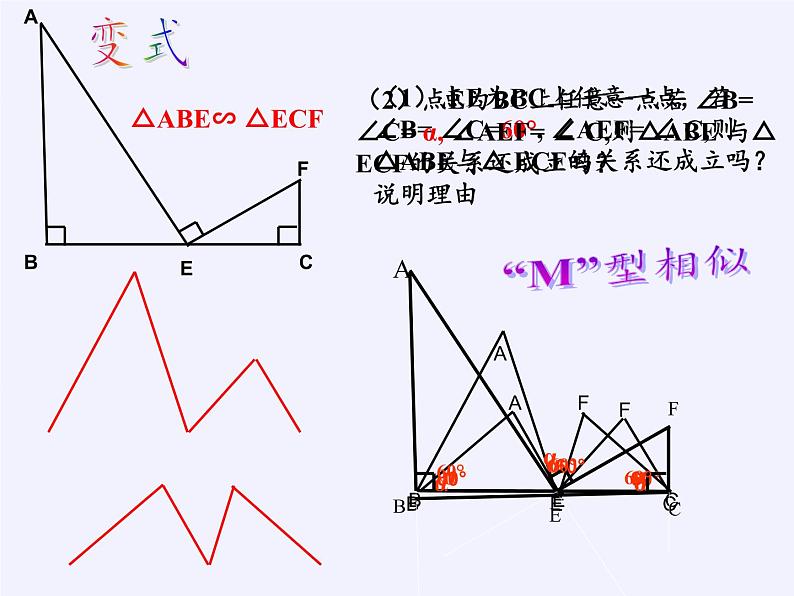
（1）点E为BC上任意一点，若 ∠B= ∠C=60°, ∠AEF= ∠ C,则△ABE与△ ECF的关系还成立吗？说明理由
（2）点E为BC上任意一点若 ∠B= ∠C= α, ∠AEF= ∠ C,则△ABE 与△ ECF的关系还成立吗？
A
（1）延长BA、CF相交于点D,且E为BC的中点，若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.①找出图中的相似三角形②说出图中相等的角及边之间的关系
（2）延长BA、CF相交于点D,且E为BC的中点，若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时，上述关系还成立吗？
点拨：要善于运用类比、迁移的数学方法解决问题。
1.在矩形ABCD中,AB=4，BC=5，AF平分∠DAE,EF⊥AE，则CF =
2、如图，四边形ABCD中，AD∥BC，AB=DC=AD=6，∠ABC=70°，点E.F分别在线段AD，DC上，且∠BEF=110°，若AE=3，DF长为________．
如图，正方形ABCD边长为8，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）证明：Rt△ABM∽Rt△MCN；（2）设BM=x，四边形ABCN的面积为y，求y与x之间的函 数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；（3）当M点运动到什么位置时， Rt△ABM∽Rt△AMN？ 求此时x的值
例 : 如图，在△ABC 中，∠BAC=135°， AC = AB, AD⊥AC 交 BC 于点 D，若 AD = ， 求△ABC的面积
例 : 如图，在△ABC 中，∠BAC=135°， AC = AB,AD⊥AC 交 BC 于点 D，若 AD = ， 求△ABC的面积
一线三等角，左右两相似一线三等角，中点三相似
通过构造基本图形证相似是辅助线添加的重要方法之一