广东省深圳市龙华中英文学校八年级上学期期中数学试卷【解析版】

这是一份广东省深圳市龙华中英文学校八年级上学期期中数学试卷【解析版】，共14页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
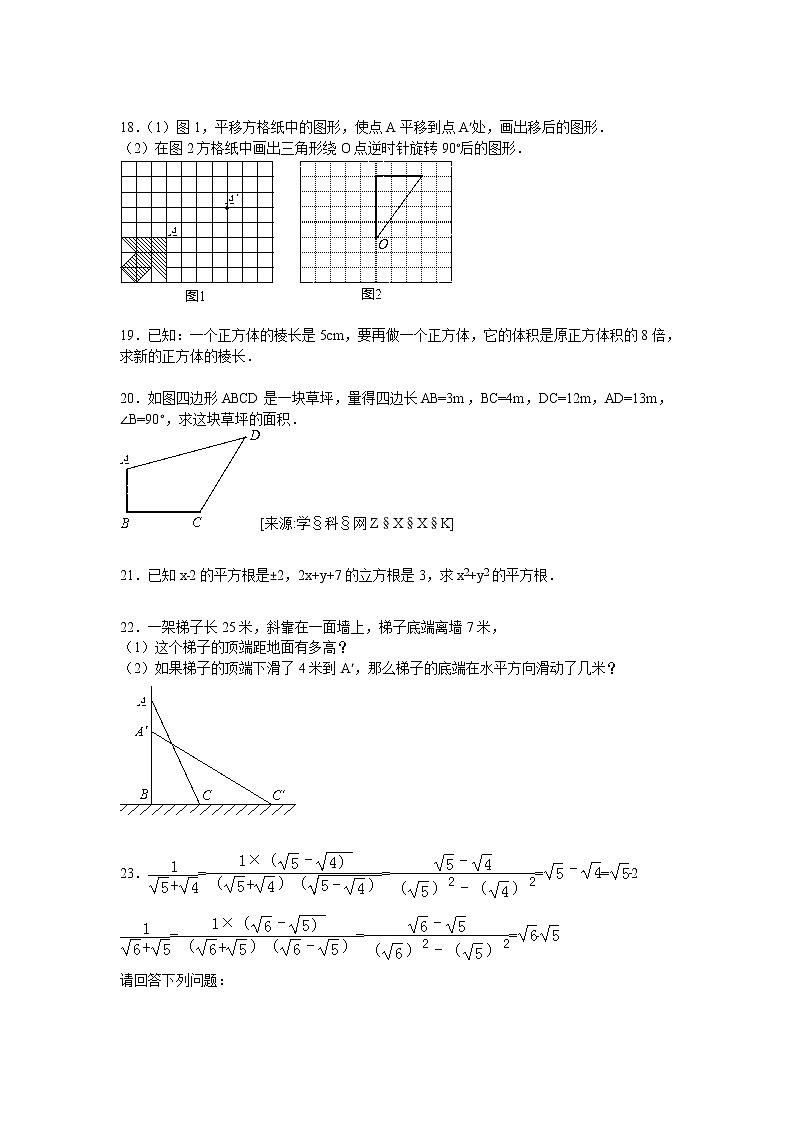
广东省深圳市龙华中英文学校八年级（上）期中数学试卷 一、单项选择题（每题3分，共30分）1．下列根式中不是最简二次根式的是(     )A． B． C． D． 2．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是(     )A． B． C． D． 3．的立方根是(     )A．4 B．±4 C．2 D．±2 4．下列运算正确的是(     )A．+= B．×= C．（﹣1）2=3﹣1 D．=5﹣3 5．若线段a，b，c能构成直角三角形，则它们的比为(     )A．2：3：4 B．3：4：6 C．5：12：13 D．4：6：7 6．和数轴上的点成一一对应关系的数是(     )A．自然数 B．有理数 C．无理数 D．实数 7．下列说法错误的是(     )A．1的平方根是±1 B．﹣1的立方根是﹣1C．是2的一个平方根 D．﹣3是的一个平方根 8．下列说法错误的是(     )A．经过平移，对应点所连的线段平行且相等B．经过平移，对应线段平行C．平移中，图形上每个点移动的距离可以不同D．平移不改变图形的形状和大小 9．一个直角三角形的两条直角边分别为5，12，则斜边上的高为(     )A． B． C． D． 10．如图，一只蚂蚁从长宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是(     )A．（3+8）cm B．10cm C．14cm D．无法确定  二、填空题（每题3分，共18分）11．立方根等于它本身的数为__________． 12．现有一长5米的梯子架靠在建筑物的墙上，它们的底部在地面的水平距离是3米，则梯子可以到达建筑物的高度是__________米． 13．若一个正数的两个平方根分别为a+2与3a﹣1，则a的值为__________． 14．若，则y=__________． 15．若a、b为实数，且满足|a﹣2|+=0，则b﹣a的值为__________． 16．我们把符合等式a2+b2=c2 的a、b、c三个称为勾股数．现请你用计算器验证下列各组的数是否勾股数．你能发现其中规律吗？请完成下列空格．3，4，5；5，12，13；7，24，25；9，40，41；11，__________，__________；…  三、解答题（共52分）17．（16分）计算题（1）（x﹣2）3=64（2）（﹣）×（3）+﹣（）2（4）（3﹣2+）÷2． 18．（1）图1，平移方格纸中的图形，使点A平移到点A′处，画出移后的图形．（2）在图2方格纸中画出三角形绕O点逆时针旋转90°后的图形． 19．已知：一个正方体的棱长是5cm，要再做一个正方体，它的体积是原正方体积的8倍，求新的正方体的棱长． 20．如图四边形ABCD是一块草坪，量得四边长AB=3m，BC=4m，DC=12m，AD=13m，∠B=90°，求这块草坪的面积．[来源:学§科§网Z§X§X§K] 21．已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根． 22．一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米到A′，那么梯子的底端在水平方向滑动了几米？ 23．====﹣2===﹣请回答下列问题：（1）观察上面的解题过程．请直接写出结果．=__________（2）利用上面提供的信息请化简：+++…+的值．  广东省深圳市龙华中八年级（上）期中数学试卷  一、单项选择题（每题3分，共30分）1．下列根式中不是最简二次根式的是(     )A． B． C． D．【考点】最简二次根式． 【分析】找到被开方数中含有开得尽方的因数的式子即可．【解答】解：各选项中只有选项C、=2，不是最简二次根式，故选：C．[来源:学科网]【点评】最简二次根式必须满足两个条件：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式．[来源:学科网ZXXK] 2．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是(     )A． B． C． D．【考点】生活中的平移现象． 【分析】根据平移的性质，结合图形对选项进行一一分析，选出正确答案．【解答】解：A、图形的形状和大小没有变化，符合平移的性质，属于平移得到；B、图形的大小发生变化，不符合平移的性质，不属于平移得到；C、图形的方向发生变化，不符合平移的性质，不属于平移得到；D、图形由轴对称得到，不属于平移得到．故选A．【点评】本题考查平移的基本性质，平移不改变图形的形状、大小和方向．注意结合图形解题的思想． 3．的立方根是(     )A．4 B．±4 C．2 D．±2【考点】立方根；算术平方根． 【专题】常规题型．【分析】如果一个数x的立方等于a，那么x是a的立方根，根据此定义求解即可．根据算术平方根的定义可知64的算术平方根是8，而8的立方根是2，由此就求出了这个数的立方根．【解答】解：∵64的算术平方根是8，8的立方根是2，∴这个数的立方根是2．故选C．【点评】本题主要考查了立方根的概念的运用．如果一个数x的立方等于a，即x的三次方等于a（x3=a），那么这个数x就叫做a的立方根，也叫做三次方根．读作“三次根号a”其中，a叫做被开方数，3叫做根指数． 4．下列运算正确的是(     )A．+= B．×= C．（﹣1）2=3﹣1 D．=5﹣3【考点】实数的运算． 【分析】A、B、C、D利用根式的运算顺序及运算法则、公式等计算即可求解．【解答】解：A、不是同类二次根式，不能合并，故选项错误；B、×=，故选项正确；C、是完全平方公式，应等于4﹣2，故选项错误；D、应该等于，故选项错误；故选B．【点评】本题考查的是二次根式的运算能力．注意：要正确掌握运算顺序及运算法则、公式等．[来源:学科网]5．若线段a，b，c能构成直角三角形，则它们的比为(     )A．2：3：4 B．3：4：6 C．5：12：13 D．4：6：7【考点】勾股定理的逆定理． 【分析】欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．【解答】解：A、22+32≠42，不能构成直角三角形，故错误；B、32+42≠62，不能构成直角三角形，故错误；C、52+122=132，能构成直角三角形，故正确；D、42+62≠72，不能构成直角三角形，故错误．故选C．【点评】解答此题要用到勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形． 6．和数轴上的点成一一对应关系的数是(     )A．自然数 B．有理数 C．无理数 D．实数【考点】实数与数轴． 【分析】根据数轴特点，数轴上的点都表示一个实数，实数都可以用数轴上的点来表示．【解答】解：∵任何实数都可以用数轴上的点来表示，数轴上的任何一点都表示一个实数，[来源:学科网ZXXK]∴和数轴上的点成一一对应关系的数是实数．故选：D．【点评】此题考查了实数和数轴上的点之间的关系：实数和数轴上的是一一对应关系． 7．下列说法错误的是(     )A．1的平方根是±1 B．﹣1的立方根是﹣1C．是2的一个平方根 D．﹣3是的一个平方根【考点】平方根；立方根． 【分析】根据平方根，立方根的定义，即可解答．【解答】解：A.1的平方根是±1，正确；B．﹣1的立方根是﹣1，正确； C．是2的一个平方根，正确；D．，3的平方根是±，故错误；故选：D．【点评】本题考查了平方根、立方根，解决本题的关键是熟记平方根，立方根的定义． 8．下列说法错误的是(     )A．经过平移，对应点所连的线段平行且相等B．经过平移，对应线段平行C．平移中，图形上每个点移动的距离可以不同[来源:学科网ZXXK]D．平移不改变图形的形状和大小【考点】平移的性质． 【分析】直接利用平移的性质分别分析得出答案．【解答】解：A、经过平移，对应点所连的线段平行且相等，正确，不合题意；B、经过平移，对应线段平行，正确，不合题意；C、平移中，图形上每个点移动的距离一定相同，故此选项错误，符合题意；D、平移不改变图形的形状和大小，正确，不合题意．故选：C．【点评】此题主要考查了平移的性质，正确掌握平移的性质是解题关键． 9．一个直角三角形的两条直角边分别为5，12，则斜边上的高为(     )A． B． C． D．【考点】勾股定理． 【分析】先利用勾股定理求出斜边的长，根据直角三角形的两直角边的乘积等于斜边与斜边上高的乘积（即ab=ch）这一性质可求．[来源:学。科。网Z。X。X。K]【解答】解：斜边长是：=13，2S△=5×12=13h，h=，故选C．【点评】此题主要考查了直角三角形的性质及勾股定理． 10．如图，一只蚂蚁从长宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是(     )A．（3+8）cm B．10cm C．14cm D．无法确定【考点】平面展开-最短路径问题． 【分析】根据”两点之间线段最短”，将点A和点B所在的两个面进行展开，展开为矩形，则AB为矩形的对角线，即蚂蚁所行的最短路线为AB．【解答】解：将点A和点B所在的两个面展开，则矩形的长和宽分别为6和8，故矩形对角线长AB==10，即蚂蚁所行的最短路线长是10．故选B．【点评】本题的关键是将点A和点B所在的面展开，运用勾股定理求出矩形的对角线． 二、填空题（每题3分，共18分）11．立方根等于它本身的数为1，﹣1，0．【考点】立方根． 【分析】根据立方根的意义得出即可．【解答】解：立方根等于它本身的本身的数为1，﹣1，0，故答案为：1，﹣1，0．【点评】本题考查了立方根的应用，主要考查学生的理解能力和计算能力． 12．现有一长5米的梯子架靠在建筑物的墙上，它们的底部在地面的水平距离是3米，则梯子可以到达建筑物的高度是4米．【考点】勾股定理的应用． 【分析】将梯子靠在墙上，就会构成一个直角三角形，然后利用勾股定理解答．【解答】解：根据勾股定理即可求得：=4．【点评】考查了勾股定理在实际生活中的应用． 13．若一个正数的两个平方根分别为a+2与3a﹣1，则a的值为﹣．【考点】平方根． 【专题】计算题．【分析】根据正数的平方根互为相反数，两平方根相加等于0求出a值，再求出一个平方根，平方就可以得到这个正数．【解答】解：根据题意，（a+2）+（3a﹣1）=0，解得a=﹣，故答案为﹣．【点评】本题考查了平方根的知识，属于基础题，注意利用正数的两个平方根互为相反数的性质求解． 14．若，则y=﹣8．【考点】立方根． 【分析】根据开立方运算即可．【解答】解：∵=﹣2，∴y=﹣8．故答案为：﹣8．【点评】本题考查了开立方运算，如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．这就是说，如果x3=a，那么x叫做a的立方根． 15．若a、b为实数，且满足|a﹣2|+=0，则b﹣a的值为﹣2．【考点】非负数的性质：算术平方根；非负数的性质：绝对值． 【分析】根据非负数的性质列式求出a、b的值，然后代入代数式进行计算即可得解．【解答】解：由题意得，a﹣2=0，﹣b2=0，解得a=2，b=0，所以，b﹣a=0﹣2=﹣2．故答案为：﹣2．【点评】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0． 16．我们把符合等式a2+b2=c2 的a、b、c三个称为勾股数．现请你用计算器验证下列各组的数是否勾股数．你能发现其中规律吗？请完成下列空格．3，4，5；5，12，13；7，24，25；9，40，41；[来源:学#科#网Z#X#X#K]11，60，61；…【考点】勾股数． 【专题】规律型．【分析】通过观察，得这组勾股数用n表示为：2n+1，2n2+2n，2n2+2n+1，据此求解．【解答】解：先用计算机验证是勾股数；通过观察得到：这组勾股数用n表示为：2n+1，2n2+2n，2n2+2n+1，11是第5组勾股数的第一个小数，所以其它2个数为：2×52+2×5=60，2×52+2×5+1=61，故答案为：60、61．【点评】此题考查的知识点是勾股数，关键是首先通过计算得是勾股数，再观察得出规律，据规律求解． 三、解答题（共52分）17．（16分）计算题（1）（x﹣2）3=64（2）（﹣）×（3）+﹣（）2（4）（3﹣2+）÷2．【考点】实数的运算；立方根． 【专题】计算题．【分析】（1）方程开立方即可求出x的值；（2）原式利用乘法分配律计算即可得到结果；[来源:学|科|网]（3）原式利用二次根式的性质，立方根及平方根定义计算即可得到结果；（4）原式利用多项式除以单项式法则计算即可得到结果．【解答】解：（1）开立方得：x﹣2=4，解得：x=6；（2）原式=﹣=9﹣12=﹣3；（3）原式=6+3﹣5=4；（4）原式=×2﹣1+×4=3﹣1+2=4．【点评】此题考查了实数的运算，以及立方根，熟练掌握运算法则是解本题的关键． 18．（1）图1，平移方格纸中的图形，使点A平移到点A′处，画出移后的图形．（2）在图2方格纸中画出三角形绕O点逆时针旋转90°后的图形．【考点】作图-旋转变换；利用平移设计图案． 【专题】作图题．【分析】（1）利用网格特点和平移的性质画图；（2）利用网格特点和旋转的性质画图．【解答】解：（1）如图1：（2）如图2：【点评】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换． 19．已知：一个正方体的棱长是5cm，要再做一个正方体，它的体积是原正方体积的8倍，求新的正方体的棱长．【考点】立方根． 【专题】应用题．【分析】由于新正方体的体积等于原正方体积的8倍，设新正方形的棱长为xcm，根据体积公式列关系式求解即可．【解答】解：设新正方形的棱长为x cm，则新正方体体积为x3cm3，依题意得：x3=8×53=（2×5）3，∴x=10（cm）．答：新正方体的棱长为10cm．【点评】本题考查正方体的体积公式求法和依题意列代数式求值的能力． 20．如图四边形ABCD是一块草坪，量得四边长AB=3m，BC=4m，DC=12m，AD=13m，∠B=90°，求这块草坪的面积．【考点】勾股定理的应用；三角形的面积． 【专题】应用题．【分析】连接AC，由∠B=90°，AB=3cm，BC=4cm可知AC=5cm；由AC、AD、CD的长可判断出△ACD是直角三角形，根据两三角形的面积可求出草坪的面积．【解答】解：在Rt△ABC中，AB=3m，BC=4m，∠B=90°由勾股定理得AB2+BC2=AC2∴AC=5m在△ADC中，AC=5m，DC=12m，AD=13m∴AC2+DC2=169，AD2=169∴AC2+DC2=AD2∠ACD=90°四边形的面积=SRt△ABC+SRt△ADC===36（m2）答：这块草坪的面积是36m2．[来源:Zxxk.Com]【点评】本题是勾股定理在实际中的应用，比较简单． 21．已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根．【考点】立方根；平方根． 【分析】先运用立方根和平方根的定义求出x与y的值，再求出x2+y2的平方根．【解答】解：∵x﹣2的平方根是±2，2x+y+7的立方根是3，∴x﹣2=22，2x+y+7=27，解得x=6，y=8，∴x2+y2=62+82=100，∴x2+y2的平方根是±10．【点评】本题主要考查了立方根和平方根，解题的关键是正确求出x与y的值． 22．一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米到A′，那么梯子的底端在水平方向滑动了几米？【考点】勾股定理的应用． 【专题】几何图形问题．【分析】（1）利用勾股定理直接得出AB的长即可；（2）利用勾股定理直接得出BC′的长，进而得出答案．【解答】解：（1）由题意得：AC=25米，BC=7米，AB==24（米），答：这个梯子的顶端距地面有24米； （2）由题意得：BA′=20米，BC′==15（米），则：CC′=15﹣7=8（米），答：梯子的底端在水平方向滑动了8米．【点评】此题主要考查了勾股定理的应用，熟练利用勾股定理是解题关键． 23．====﹣2===﹣请回答下列问题：（1）观察上面的解题过程．请直接写出结果．=﹣（2）利用上面提供的信息请化简：+++…+的值．【考点】分母有理化． 【分析】（1）利用已知数据变化规律直接得出答案；（2）利用分母有理化的规律将原式化简进而求出即可．【解答】解：（1）==﹣；故答案为：﹣； （2）+++…+=﹣1+﹣+﹣+…+﹣=﹣1=2﹣1．【点评】此题主要考查了分母有理化，正确化简二次根式是解题关键．