北师大版八年级下册第五章 分式与分式方程综合与测试练习

这是一份北师大版八年级下册第五章 分式与分式方程综合与测试练习，文件包含《分式》全章复习与巩固基础巩固练习doc、《分式》全章复习与巩固基础知识讲解doc等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
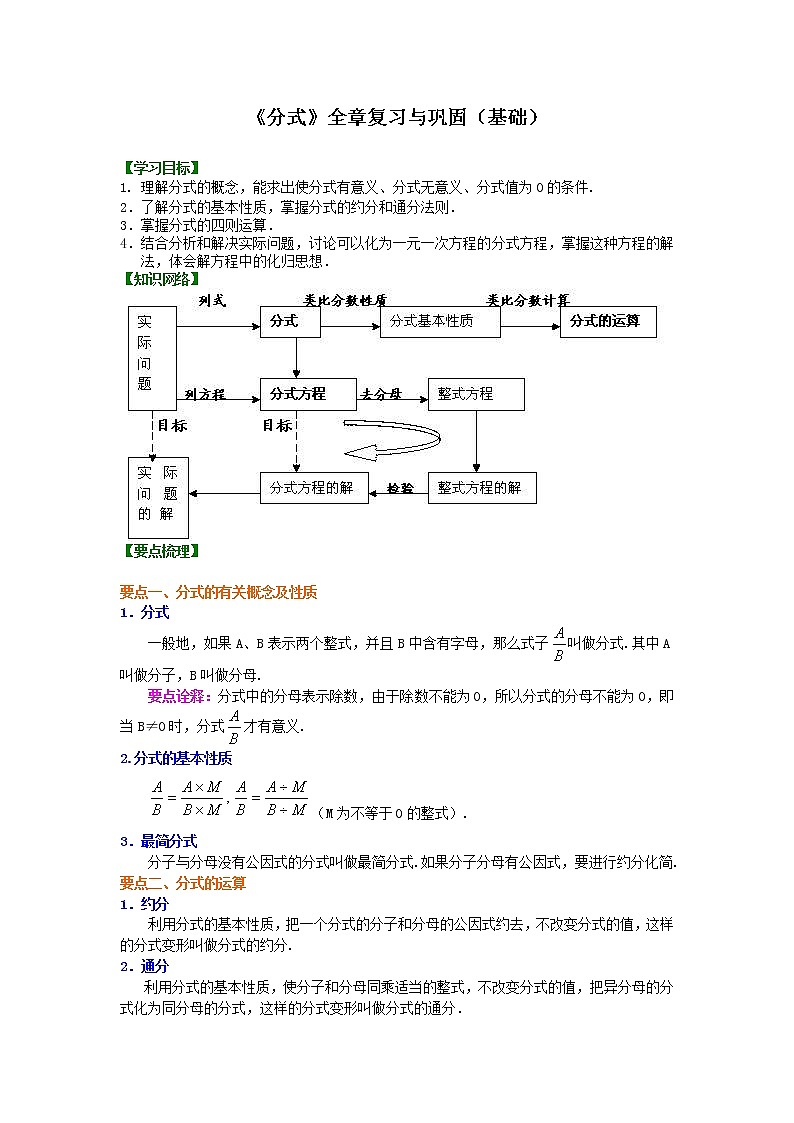
《分式》全章复习与巩固（基础） 【学习目标】1. 理解分式的概念，能求出使分式有意义、分式无意义、分式值为0的条件. 2．了解分式的基本性质，掌握分式的约分和通分法则． 3．掌握分式的四则运算．4．结合分析和解决实际问题，讨论可以化为一元一次方程的分式方程，掌握这种方程的解法，体会解方程中的化归思想．【知识网络】【要点梳理】 要点一、分式的有关概念及性质1．分式一般地，如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式.其中A叫做分子，B叫做分母.要点诠释：分式中的分母表示除数，由于除数不能为0，所以分式的分母不能为0，即当B≠0时，分式才有意义.2.分式的基本性质
　　（M为不等于0的整式）.
3．最简分式分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式，要进行约分化简.要点二、分式的运算1．约分　利用分式的基本性质，把一个分式的分子和分母的公因式约去，不改变分式的值，这样的分式变形叫做分式的约分.2．通分利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把异分母的分式化为同分母的分式，这样的分式变形叫做分式的通分．　　3．基本运算法则　 分式的运算法则与分数的运算法则类似,具体运算法则如下:（1）加减运算   ；同分母的分式相加减，分母不变，把分子相加减. ；异分母的分式相加减，先通分，变为同分母的分式，再加减. （2）乘法运算   ，其中是整式，.两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.（3）除法运算  ，其中是整式，.两个分式相除，把除式的分子和分母颠倒位置后，与被除式相乘.（4）乘方运算               分式的乘方，把分子、分母分别乘方.
4.分式的混合运算顺序　先算乘方，再算乘除，最后加减，有括号先算括号里面的.要点三、分式方程1．分式方程的概念分母中含有未知数的方程叫做分式方程．2．分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程． 3．分式方程的增根问题增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根－－－增根.要点诠释：因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解.要点四、分式方程的应用
　　列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解.【典型例题】类型一、分式及其基本性质 1、在中，分式的个数是（     ）A.2            B.3              C.4           D.5【答案】C；【解析】是分式.【总结升华】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式． 2、当为何值时，分式的值为0？【思路点拨】先求出使分子为0的字母的值，再检验这个值是否使分母的值等于0，当它使分母的值不等于0时，这个值就是要求的字母的值．【答案与解析】解： 要使分式的值为0，必须满足分子等于0且分母不等于0． 由题意，得  解得．∴  当时，分式的值为0．【总结升华】分式的值为0的条件是：分子为0，且分母不为0，即只有在分式有意义的前提下，才能考虑分式值的情况. 举一反三：【变式】（1）若分式的值等于零，则＝_______；
　　　　（2）当________时，分式没有意义．
【答案】（1）由＝0，得. 当＝2时－2＝0，所以＝－2；　　　　　　
　　　 （2）当，即＝1时，分式没有意义．类型二、分式运算 3、计算：．【答案与解析】解：．【总结升华】本题有两处易错：一是不按运算顺序运算，把和先约分；二是将和约分后的结果错认为是1．因此正确掌握运算顺序与符号法则是解题的关键．举一反三：【变式】（2020•滨州）化简：÷（﹣）【答案】解：原式=÷=•=﹣．类型三、分式方程的解法4、（2020•呼伦贝尔）解方程：．【思路点拨】观察可得最简公分母是（x﹣1）（x+1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【答案与解析】解：方程的两边同乘（x﹣1）（x+1），得3x+3﹣x﹣3=0，解得x=0．检验：把x=0代入（x﹣1）（x+1）=﹣1≠0．∴原方程的解为：x=0．【总结升华】本题考查了分式方程的解法，注：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．举一反三：【变式】，【答案】 解： 方程两边同乘以，得     检验：当时，最简公分母，∴是原方程的解．类型四、分式方程的应用5、（2020•东莞二模）某市为治理污水，需要铺设一条全长为600米的污水排放管道，为了尽量减少施工对城市交通所造成的影响，实际施工时，每天的工效比原计划增加20%，结果提前5天完成这一任务，原计划每天铺设多少米管道？【思路点拨】先设原计划每天铺设x米管道，则实际施工时，每天的铺设管道（1+20%）x米，由题意可得等量关系：原计划的工作时间﹣实际的工作时间=5，然后列出方程可求出结果，最后检验并作答．【答案与解析】解：设原计划每天铺设x米管道，由题意得：﹣=5，解得：x=20，经检验：x=20是原方程的解．答：原计划每天铺设20米管道．【总结升华】本题主要考查分式方程的应用，解题的关键是熟练掌握列分式方程解应用题的一般步骤：设、列、解、验、答．必须严格按照这5步进行，规范解题步骤，另外还要注意完整性：如设和答叙述要完整，要写出单位等．举一反三：【变式】小明家、王老师家、学校在同一条路上，并且小明上学要路过王老师家，小明到王老师家的路程为3 km，王老师家到学校的路程为0.5 km，由于小明的父母战斗在抗震救灾第一线，为了使他能按时到校、王老师每天骑自行车接小明上学．已知王老师骑自行车的速度是他步行速度的3倍，每天比平时步行上班多用了20 min，王老师步行的速度和骑自行车的速度各是多少?【答案】解：设王老师步行的速度为 km/h，则他骑自行车的速度为3 km/h．根据题意得：．解得：．经检验是原方程的根且符合题意．当时，．答：王老师步行的速度为5km/h，他骑自行车的速度为15km/h．