数学九年级上册3 反比例函数的应用说课课件ppt

这是一份数学九年级上册3 反比例函数的应用说课课件ppt，共22页。PPT课件主要包含了新课引入，是双曲线，知识讲解，至少为96m3，最少4h，强化训练，课堂总结，目标测试等内容，欢迎下载使用。

2.反比例函数图象是什么?
1.什么是反比例函数?
当k>0时,两支曲线分别位于第一、三象限内，在每一象限内，y随x的增大而减小；当k<0时,两支曲线分别位于第二、四象限,在每一象限内,y随x的增大而增大.
某科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地，他们沿着前进路线铺垫了若干木板，构筑了一条临时通道，从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时，随着木板面积S(m2)的变化，人和木板对地面的压强P(Pa)将如何变化?
如果人和木板对湿地地面的压力合计600N，那么 (1)用含S的代数式表示P，P是S的反比例函数吗?为什么?
解: ，P是S的反比例函数.
(2)当木板面积为0.2m2时，压强是多少?
解:当S=0.2m2时，
(3)如果要求压强不超过6000Pa，木板面积至少要多大?
如果人和木板对湿地地面的压力合计600N,那么
(4)在平面直角坐标系中,画出相应的函数图象。
注意:只需在第一象限作出函数的图象.因为S>0.
(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.
问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上（含直线P=6000与图象的交点）.
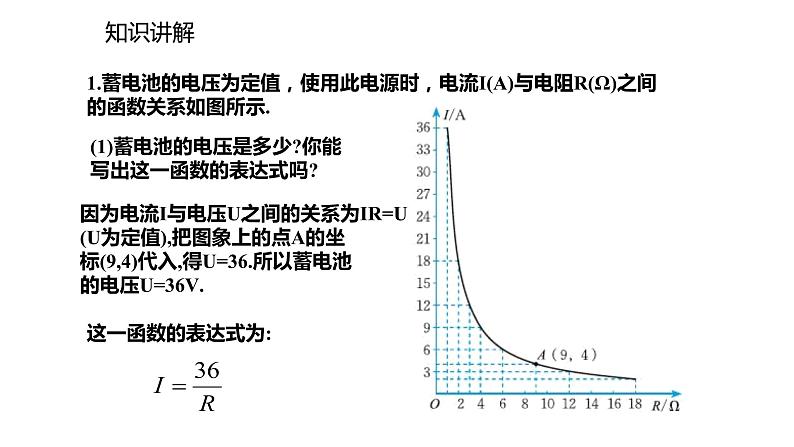
1.蓄电池的电压为定值，使用此电源时，电流I(A)与电阻R(Ω)之间的函数关系如图所示.
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
因为电流I与电压U之间的关系为IR=U(U为定值),把图象上的点A的坐标(9,4)代入,得U=36.所以蓄电池的电压U=36V.
(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
当I≤10A时,解得R≥3.6(Ω).所以可变电阻应不小于3.6Ω.
(1)分别写出这两个函数的表达式;
所求的函数表达式为:y=2x和
(2)你能求出点B的坐标吗?你是怎样求的?
B点的坐标是两个函数组成的方程组的另一个解.
（3）观察图象回答:x为何值时，反比例函数值小于一次函数值？
某蓄水池排水管的排水速度是8m3/h,6h可将满池水全部排空.
蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使排水速度达到Q(m3/h),那么将满池水排空所需的时间t(h)将如何变化?
此时所需时间t(h)将减少.
(3)写出t与Q之间的关系式;
(1)蓄水池的容积是多少?
(4)如果准备在5h内将满池水排空,那么排水速度至少为多少?
(5)已知排水管的最大排水速度为12m3/h,那么最少多长时间可将满池水全部排空?
1.在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V 时，气体的密度ρ也随之改变.ρ与V 在一定范围内满足，它的图象如图所示，则该气体的质量m为（ ） B. 5kg D.7kg
2.如图所示，P1、P2、P3是双曲线上的三个点，过这三点分别作y轴的垂线，得三个三角形OP1A1、OP2A2、OP3A3，设它们的面积分别为S1、S2、S3，则（ ） A.S1本节课我们学习了反比例函数的应用.具体步骤是：认真分析实际问题中变量之间的关系，建立反比例函数模型，进而用反比例函数的有关知识解决实际问题. 
1．在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也随之改变．密度ρ（单位：kg/m3）与体积V（单位：m3）满足函数关系式ρ= （k为常数，k≠0），其图象如图所示，则k的值为（　　）
A．9 B．-9C．4 D．-4
2.小明乘车从南充到成都，行车的速度v（km/h）和行车时间t（h）之间的函数图象是（　　）
A B C D
3.某闭合电路中，电源的电压为定值，电流强度I（A）与电阻R（Ω）成反比例关系，其函数图象如图所示，则电流强度I（A）与电阻R（Ω）的函数解析式是 ．
4.蓄电池的电压为定值，使用此电源时，电流I（A）是电阻R（Ω）的反比例函数，其图象如图所示． （1）求这个反比例函数的表达式； （2）当R=10Ω时，电流能是4A吗？为什么？
（2）当R=10Ω时，I=3.6≠4，∴电流不可能是4A.