
北师大版七年级下册第四章 三角形综合与测试单元测试课时训练
展开
北师大版初中数学七年级下册第四单元《三角形》单元测试卷(较易)
考试范围:第四章;考试时间:100分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
- 已知,,是的三条边长,化简的结果为
A. B. C. D.
- 如图,为估计池塘岸边,两点的距离,小明在池塘的一侧选取一点,测得,,则,间的距离不可能是
A.
B.
C.
D.
- 如图,下列说法错误的是
A. ,,是的内角
B. 是与相邻的角
C.
D. 的三条边分别是,,
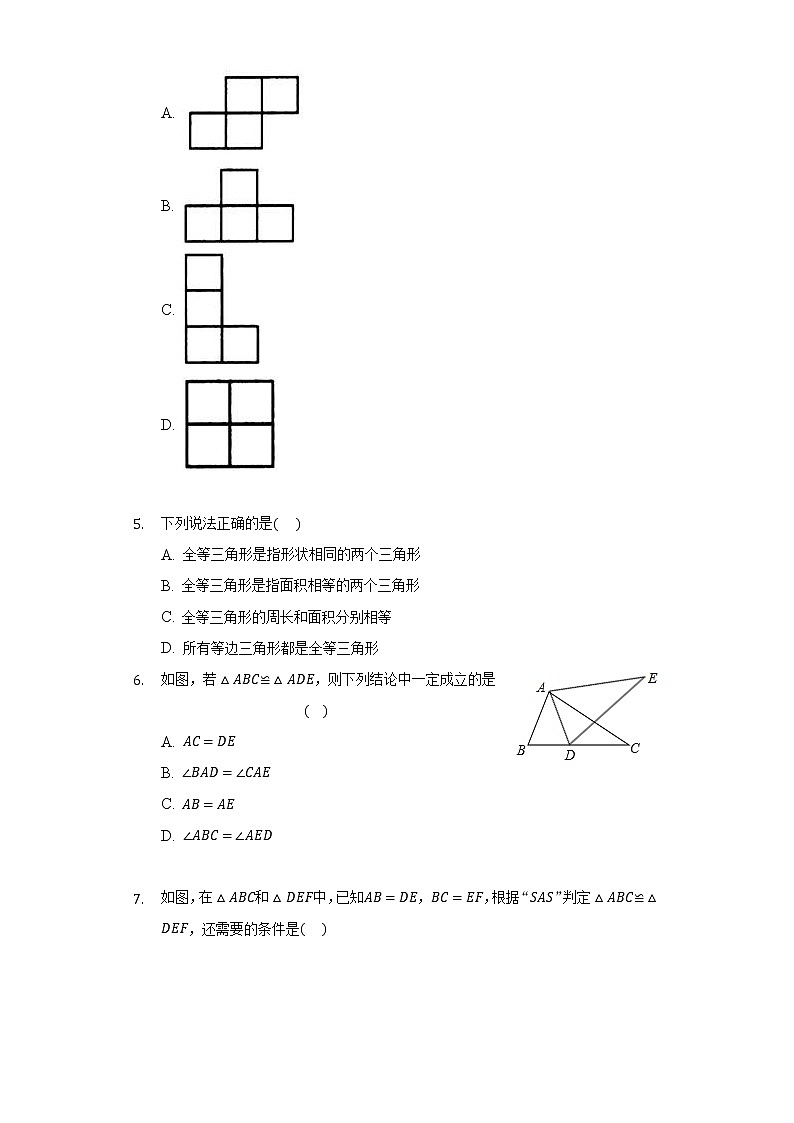
- 下列图形中,与如图所示的图形全等的是
A.
B.
C.
D.
- 下列说法正确的是
A. 全等三角形是指形状相同的两个三角形
B. 全等三角形是指面积相等的两个三角形
C. 全等三角形的周长和面积分别相等
D. 所有等边三角形都是全等三角形
- 如图,若≌,则下列结论中一定成立的是
A.
B.
C.
D.
- 如图,在和中,已知,,根据“”判定,还需要的条件是
A. B. C. D. 以上均可以
- 如图,已知,添加下列条件,不能使的是
A.
B.
C.
D.
- 如图,在格的正方形网格中,与有一条公共边且全等不与重合的格点三角形顶点在格点上的三角形共有
A. 个
B. 个
C. 个
D. 个
- 如图,中,,如果用尺规作图的方法在上确定点,使,那么符合要求的作图痕迹是
A. B.
C. D.
- 如图,在中,,以点为圆心,以任意长度为半径画弧交,于点,,分别以点,为圆心,以大于的长度为半径画弧,两弧交于点,作射线;以点为圆心,以任意长度为半径画弧交,于点,,分别以点,为圆心,以大于的长度为半径画弧,两弧交于点,作射线;若与相交于点,则的度数是
A. B. C. D.
- 如图,为了测量点到河对面的目标之间的距离,在点同侧选择了一点,测得,,然后在处立了标杆,使,,得到≌,所以测得的长就是,两点间的距离,这里判定≌的理由是
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
- 如图,,其中,,则 .
- 如图,在中,,,,平分交于点,在上截取,则的周长为 _____
- 如图,≌若,,则的大小为______度.
|
- 如图,在中,,分别是边上的中线和高,,,则 .
|
三、解答题(本大题共8小题,共72.0分)
- 如图所示,在中,,,是的角平分线,点在上,且,求的度数.
- 如图,,,,
求四边形的面积
在轴上找一点,使三角形的面积等于四边形面积的一半求点坐标.
- 如图,≌,点在线段上,点在延长线上,,求证:.
- 如图,将等腰直角三角形的直角顶点置于直线上,过,两点分别作直线的垂线,垂足分别为,,求证:.
|
- 如图,已知线段.
按要求作图:反向延长线段至,使得.
在的条件下,取的中点,求的长,
- 如图,已知,,求证:.
- 如图,中,是边上一点,是的中点,过点作的平行线交的延长线于,且,连接.
求证:≌;
若,试判断四边形的形状,并证明你的结论.
- 如图,已知线段、相交于点,连接、,则我们把形如这样的图形称为“字型”.
求证:;
如图,若和的平分线和相交于点,且与、分别相交于点、.
以线段为边的“字型”有______个,以点为交点的“字型”有______个;
若,,求的度数;
若角平分线中角的关系改为“,”,试探究与、之间存在的数量关系,并证明理由.
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了三角形的三边关系及绝对值性质,利用三角形三边关系去绝对值符号是本题解题的关键。先根据三角形的三边关系判断出与的符号,再去绝对值符号,合并同类项即可。
【解答】
解:、、为的三条边长
故选D.
2.【答案】
【解析】
【分析】
此题考查的是三角形三边关系定理利用三角形两边之和大于第三边,两边之差小于第三边可得出答案.
【解答】
解:,
,
所以不可能是.
故选D.
3.【答案】
【解析】.
4.【答案】
【解析】分析
此题主要考查了全等图形,关键是掌握全等图形的定义.
根据能够完全重合的两个图形叫做全等图形可得答案.
详解
解:与题图中的图形全等的是中的图形,
故选B.
5.【答案】
【解析】分析
本题考查了全等三角形的定义和性质,解题关键是掌握全等三角形的性质解题时,根据全等三角形的定义和性质对各选项进行判断即可.
详解
解:全等三角形是指形状和大小完全相同的两个三角形,故此选项错误;
B.面积相等的两个三角形不一定是全等三角形,故此选项错误;
C.全等三角形的周长和面积分别相等,故此选项正确;
D.等边三角形的边长不一定相等,因此等边三角形不一定是全等三角形,故此选项错误.
故选C.
6.【答案】
【解析】
【分析】
本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.根据全等三角形的性质即可得到结论.
【解答】
解:≌,
,,,,
,
即故A,,选项错误,选项正确,
故选:.
7.【答案】
【解析】要利用判定,已知,,还需夹角相等,即,故选B.
8.【答案】
【解析】
【分析】
本题考查三角形全等的判定方法有关知识,本题要判定≌,已知,,具备了一组边一组角对应相等,对选项一一分析,选出正确答案.
【解答】
解:添加,不能判定≌,故符合题意;
B.添加,可根据判定≌,故不符合题意;
C.添加,可根据判定≌,故不符合题意;
D.添加,可根据判定≌,故不符合题意.
故选A.
9.【答案】
【解析】解:以为公共边可画出,,三个三角形和原三角形全等.
以为公共边可画出三个三角形,,和原三角形全等.
以为公共边可画出一个三角形和原三角形全等,
所以可画出个.
故选:.
可以以和为公共边分别画出个,不可以,故可求出结果.
本题考查全等三角形的性质,三条对应边分别相等,以及格点的概念.
10.【答案】
【解析】解:,而,
,
点在的垂直平分线上,
即点为的垂直平分线与的交点.
故选:.
由和易得,根据线段垂直平分线定理的逆定理可得,点在的垂直平分线上,进而得出结论.
本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
11.【答案】
【解析】解:由作图可知:,,
,
,
,
故选:.
由作图可知:,,根据计算即可.
本题考查作图复杂作图,三角形内角和定理等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型.
12.【答案】
【解析】
【分析】
此题主要考查了全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.利用全等三角形的判定方法进行分析即可.
【解答】
解:在和中,
,
≌,
故选D.
13.【答案】
【解析】
【分析】本题本题主要考查全等三角形的应用,根据全等三角形的性质即可得出.
【解答】
解:,,
.
14.【答案】
【解析】
【分析】
本题考查了全等三角形的性质与判定,解决本题的关键是证明≌利用已知条件证明≌,得到,从而,即可求得的周长.
【解答】
解:是的平分线,
,
在和中,
,,,
≌,
,,
,
的周长.
15.【答案】
【解析】解:≌,
,,
,
,
故答案为:.
根据全等三角形的性质得到,,根据三角形内角和定理求出,计算即可.
本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.
16.【答案】
【解析】略
17.【答案】解:,,
,
平分,
,
,
.
【解析】首先利用三角形内角和定理得出的度数,再利用平行线的性质以及角平分线的定义分析得出答案.
此题主要考查了三角形内角和定理以及平行线的性质以及角平分线的定义,正确掌握相关性质是解题关键.
18.【答案】解:分别过、两点作轴的垂线,垂足分别为、,
则
;
设的边上高为,
则由,得
,
解得
又点在轴上,
或.
【解析】本题主要考查了坐标与图形的性质及面积的计算,熟练掌握求不规则图形面积的一般方法,即割补法是解题的关键.
分别过、两点作轴的垂线,将图形分割为两个直角三角形和一个直角梯形求面积和即可;
设的边上高为,根据,列方程求,再根据所求点可能在轴正半轴或负半轴,分别写出点的坐标.
19.【答案】证明:≌,
,
,
,
.
【解析】根据≌得到,然后利用得到,利用同位角相等,两直线平行证得结论.
考查了全等三角形的性质,解题的关键是了解全等三角形的对应角相等,难度不大.
20.【答案】解:由题意知,
,
.
在与中,
≌.
.
【解析】根据这两个三角形中的数量关系由证明:≌,从而得出.
本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:、、、、.
注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
21.【答案】解:如图,
反向延长线段至,使得.
在的条件下,
,,
是的中点,
,
.
答:的长为.
【解析】反向延长线段至,使得即可;
在的条件下,取的中点,即可求的长,
本题考查了作图复杂作图,解决本题的关键是准确画图.
22.【答案】证明:,
在和中
≌
.
【解析】根据,得到,利用定理证明≌,根据全等三角形的性质证明即可.
本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.
23.【答案】证明:是的中点,
,
,
,,
≌;
连接,
,,
四边形是平行四边形,
≌,
,
,
四边形是平行四边形,
,
,
,
四边形是矩形.
【解析】由得,继而结合、即可判定全等;
根据,且是边上的中线可得,由四边形是矩形可得答案.
此题主要考查了平行四边形的判定以及全等三角形的判定与性质、矩形的判定、三角形中线的性质等知识点,熟练掌握平行四边形的判定是解题关键.
24.【答案】证明见解析;
,;
;
,理由见解析.
【解析】证明:在图中,有,,
,
;
解:;;
故答案为:,;
以为交点“字型”中,有,
以为交点“字型”中,有,
,
、分别平分和,
,,
,
,,
;
,其理由是:
,,
,,
以为交点“字型”中,有,
以为交点“字型”中,有
,
.
,
.
根据三角形的内角和即可得到结论;
以线段为边的“字型”有个,以点为交点的“字型”有个;
根据角平分线的定义得到,,再根据三角形内角和定理得到,,两等式相减得到,即,然后把,代入计算即可;
与的证明方法一样得到.
本题考查了三角形内角和定理:三角形内角和是也考查了角平分线的定义.
北师大版初中数学七年级下册期末测试卷(较易)(含答案解析): 这是一份北师大版初中数学七年级下册期末测试卷(较易)(含答案解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版初中数学七年级下册期中测试卷(较易)(含答案解析): 这是一份北师大版初中数学七年级下册期中测试卷(较易)(含答案解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021学年第4章 相似三角形综合与测试单元测试习题: 这是一份2021学年第4章 相似三角形综合与测试单元测试习题,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。