高中数学人教A版 (2019)必修 第二册7.3* 复数的三角表示课后作业题

这是一份高中数学人教A版 (2019)必修 第二册7.3* 复数的三角表示课后作业题，共11页。试卷主要包含了复数的三角表示，复数的辅角等内容，欢迎下载使用。
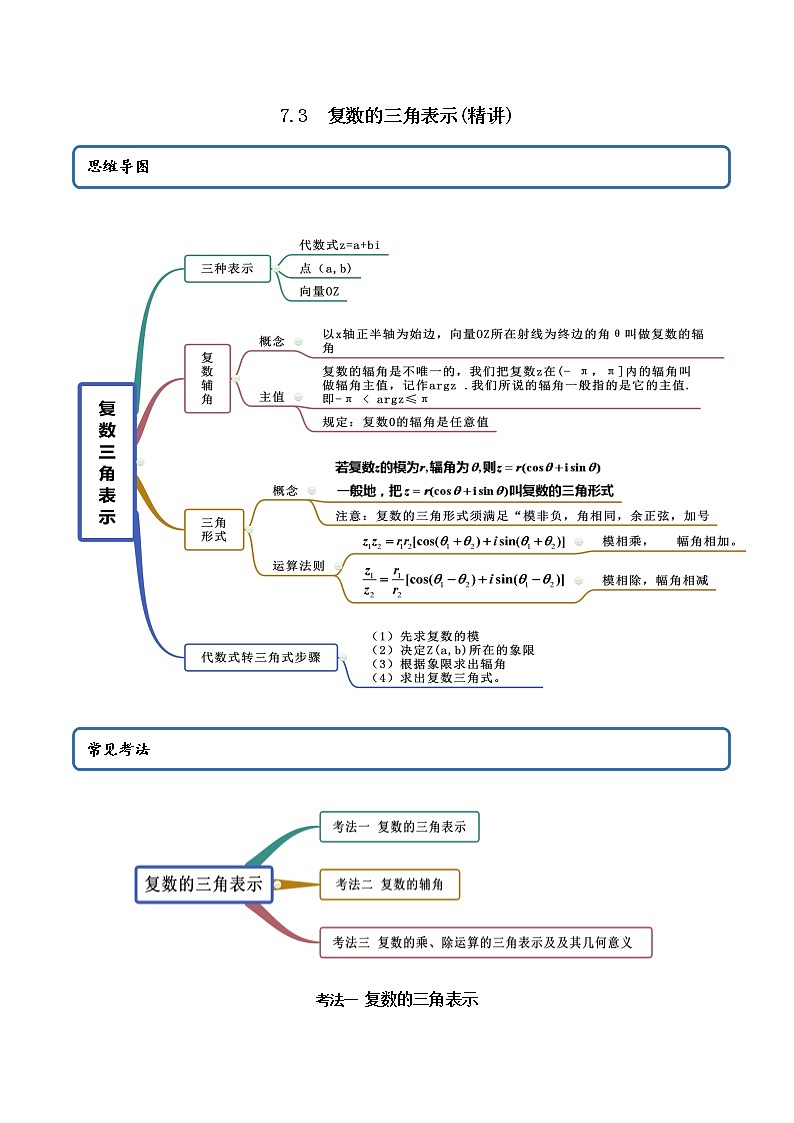
7.3  复数的三角表示(精讲)考法一 复数的三角表示 【例1-1】(2020·全国高一课时练习)把下列复数的代数形式化成三角形式.(1)；(2).【答案】(1)(2)【解析】(1).因为与对应的点在第四象限，所以，所以.(2).因为与对应的点在第四象限，所以，所以.【例1-2】．(2020·全国高一课时练习)把下列复数的三角形式化成代数形式.(1)；(2).【答案】(1)(2)【解析】(1).(2). 【举一反三】1．(2020·全国高一课时练习)画出下列复数对应的向量，并把这些复数表示成三角形式：(1)；(2).【答案】(1)作图见解析;(2)作图见解析;【解析】(1)复数对应的向量如图所示，则.因为与对应的点在第一象限，所以.于是.(2)复数对应的向量如图所示，则.因为与对应的点在第四象限，所以.于是.当然，把一个复数表示成三角形式时，辐角不一定取主值.例如也是的三角形式.2．(2020·全国高一课时练习)将下列各复数的三角形式转化为代数形式：(1)；(2)；(3)；(4).【答案】(1)(2)(3)(4)【解析】(1).(2).(3).(4).3．(2020·全国高一课时练习)将下列各复数转化为三角形式(辐角取辐角主值)：(1)；(2)-2i；(3)；(4).【答案】(1)；(2)；(3)；(4)【解析】(1)∵，，，又，∴，∴.(2)∵，，，又，∴，∴.(3)∵，，，又，∴，∴.(4)∵，，，又，∴.∴.考法二 复数的辅角 【例2】(2020·全国高一课时练习)复数的辐角主值为(    )A． B． C． D．【答案】D【解析】,故复数z的辐角主值为.故选：D【举一反三】1.(2020·全国)复数，由向量绕原点逆时针方向旋转而得到.则的值为(    )A． B． C． D．【答案】C【解析】,,所以复数在第二象限，设幅角为， 故选：C2．(2020·全国高一课时练习)若复数(i为虚数单位)，则为(    )A． B．120° C．240° D．210°【答案】C【解析】由，得复数z对应的点在第三象限，且，所以.故选：C.3．(2020·辽宁辽师大附中高一期末)把复数z1与z2对应的向量分别按逆时针方向旋转和后，重合于向量且模相等，已知，则复数的代数式和它的辐角主值分别是(    )A．， B． C． D．【答案】B【解析】由题可知，则，，可知对应的坐标为，则它的辐角主值为.故选：B.考法三 复数的乘、除运算的三角表示及及其几何意义【例3】(2020·全国高一课时练习)计算下列各式：(1)；(2)；(3)；(4).【答案】(1)；(2)；(3)；(4)【解析】(1).(2).(3).(4).【举一反三】1．(2020·全国高一课时练习)(    )A． B． C． D．【答案】C【解析】.故选：C2．(2020·全国高一课时练习)(    )A．3 B． C． D．【答案】B【解析】.故选：B3．(2020·全国高一课时练习)(    )A． B． C． D．【答案】C【解析】.故选：C.4．(2020·全国高一课时练习)计算下列各式，并作出几何解释：(1)(2)(3)(4).【答案】(1)-4，几何解释见解析  (2)，几何解释见解析  (3)，几何解释见解析  (4)，几何解释见解析【解析】(1)原式.几何解释：设，作与对应的向量，然后把向量绕原点O按逆时针方向旋转，再将其长度伸长为原来的倍，得到一个长度为4,辐角为π的向量，则即为积所对应的向量.(2)原式.几何解释：设，作与对应的向量，然后把向量绕原点O按逆时针方向旋转315°，再将其长度缩短为原来的，得到一个长度为、辐角为 的向量，则即为积所对应的向量.(3)原式.几何解释：设，作与对应的向量，然后把向量绕原点0按顺时针方向旋转，再将其长度缩短为原来的，得到一个长度为，辐角为的向量，则即为所对应的向量.(4)原式.几何解释：设，作与对应的向量，然后把向量绕原点0按顺时针方向旋转，再将其长度缩短为原来的，得到一个长度为，辐角为的向量，则即为所对应的向量.