高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率同步达标检测题

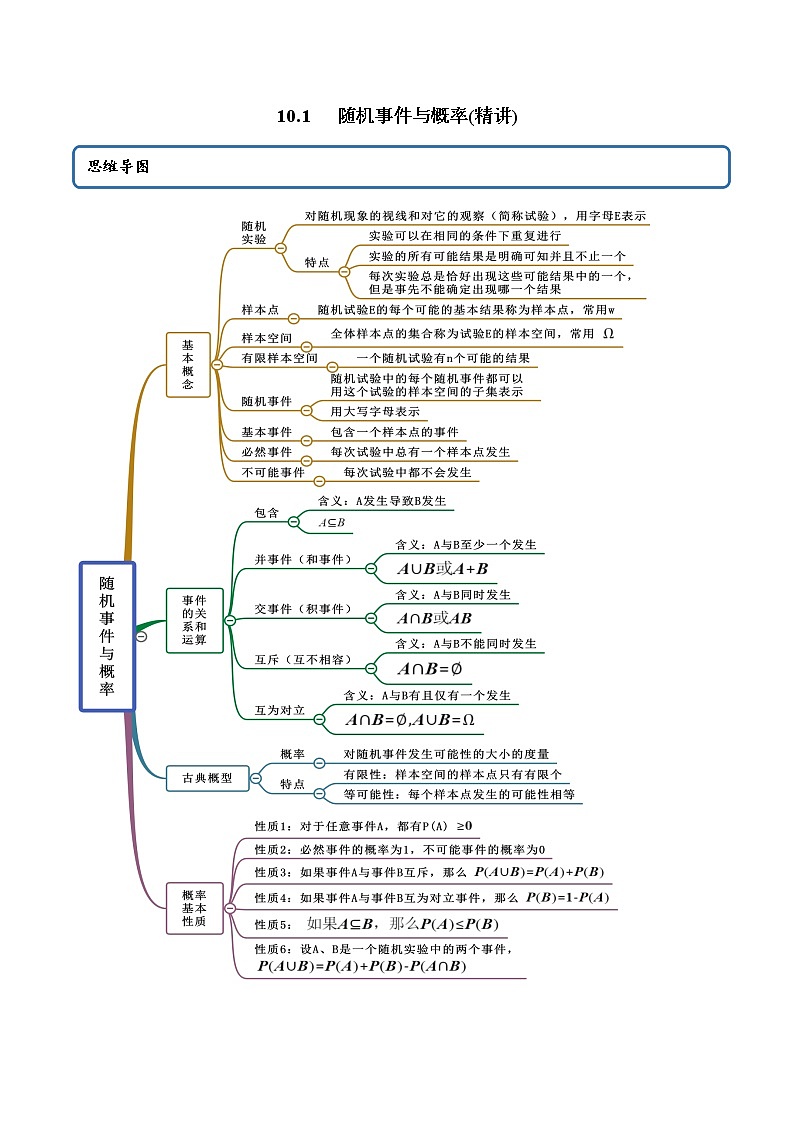
10.1   随机事件与概率(精讲)

考法一 有限样本空间与随机事件

【例1-1】(2021·全国高一)给出下列四个命题：

①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件；

②“当x为某一实数时，可使x2≤0”是不可能事件；

③“明天天津市要下雨”是必然事件；

④“从100个灯泡(含有10个次品)中取出5个，5个全是次品”是随机事件．

其中正确命题的个数是(    )

A．0 B．1

C．2 D．3

【答案】C

【解析】对于①，三个球全部放入两个盒子，有两种情况：1+2和3+0，故必有一个盒子有一个以上的球，所以该事件是必然事件，①正确；

对于②，x=0时x2=0，所以该事件不是不可能事件，②错误；

对于③，“明天天津市要下雨”是偶然事件，所以该事件是随机事件，③错误；

对于④，“从100个灯泡(含有10个次品)中取出5个，5个全是次品”，发生与否是随机的，所以该事件是随机事件，④正确．故正确命题有2个.故选：C．

【例1-2】(2020·全国高一)袋子中有4个大小和质地相同的球，标号为1，2，3，4，从中随机摸出一个球，记录球的编号，先后摸两次.

(1)若第一次摸出的球不放回，写出试验的样本空间；

(2)若第一次摸出的球放回，写出试验的样本空间.

【答案】(1)详见解析(2)详见解析

【解析】m表示第一次摸出球的编号，用n表示第二次摸出球的编号，则样本点可用，表示.

(1)若第一次摸出的球不放回，则，此时的样本空间可表示为

，共有12个样本点.

(2)若第一次摸出的球放回，则m，n可以相同.此时试验的样本空间可表示为，共有16个样本点.

【举一反三】

1．(2021·全国高一课时练习)下列事件中，随机事件的个数为(    )

①连续两次抛掷一枚骰子，两次都出现2点向上；②13个人中至少有两个人生肖相同；③某人买彩票中奖；④在标准大气压下，水加热到90℃会沸腾.

A．1个 B．2个 C．3个 D．4个

【答案】B

【解析】抛掷一枚骰子，每一面出现都是随机的，所以①是随机事件；

一年只有12生肖，所以13个人中至少有两个人生肖相同是必然事件，所以②是必然事件；

购买彩票号码是随机的，某人买彩票中奖也是随机的，所以③是随机事件；

在标准大气压下，水加热到100℃才会沸腾.故④是不可能事件故选：B

2．(多选)(2020·全国高一单元测试)下列事件中，是随机事件的是(    )

A．年月日，北京市不下雨

B．在标准大气压下，水在时结冰

C．从标有，，，的张号签中任取一张，恰为号签

D．若，则

【答案】AC

【解析】A选项与C选项为随机事件，B为不可能事件，D为必然事件．故选：AC．

3．(2020·全国高一课时练习)写出下列各随机试验的样本空间：

(1)采用抽签的方式，随机选择一名同学，并记录其性别；

(2)采用抽签的方式，随机选择一名同学，观察其ABO血型；

(3)随机选择一个有两个小孩的家庭，观察两个孩子的性别；

(4)射击靶3次，观察各次射击中靶或脱靶情况；

(5)射击靶3次，观察中靶的次数.

【答案】(1)详见解析(2)详见解析(3)详见解析(4)详见解析(5)详见解析

【解析】解：(1)一名同学的性别有两种可能结果：男或女.故该试验的样本室间可以表示为{男，女}；

(2)一名同学的血型有四种可能结果：A型、B型、AB型、O型.故该试验的样本空间可表示为；

(3)每个小孩的性别有男或女两种可能，两个小孩的性别情况有四种可能，故该试验的样本空间可表示为{(男、男)，(男，女)，(女，男)，(女，女)}；

(4)每次射击有中靶或脱靶两种可能，射击3次有八种可能，用1表示中靶，用0表示脱靶，该试验的样本空间可表示为；

(5)射击3次，中靶的次数可能是0，1，2，3，故该试验的样本空间可以表示为.

4．(2021·全国高一)写出下列试验的样本空间：

(1)设袋中装有4个白球和6个黑球，从中不放回逐个取出，直到白球全部取出为止，记录取球的次数；

(2)甲、乙、丙三位同学参加演讲比赛，通过抽签确定演讲的顺序，记录抽签的结果.

【答案】(1)详见解析(2)详见解析

【解析】(1)从中不放回逐个取出，直到白球全部取出为止，则取球次数为；

(2)由抽签确定演讲的顺序，抽签的结果即样本空间可表示为{(甲，乙，丙)，(甲，丙，乙)，(丙，甲，乙)，(丙，乙，甲)，(乙，甲，丙)，(乙，丙，甲)}.

考法二 事件的关系与运算

【例2-1】(2020·全国高一课时练习)盒子里有6个红球，4个白球，现从中任取3个球.设事件“1个红球和2个白球”，事件“2个红球和1个白球”，事件“至少有1个红球”，事件“既有红球又有白球”，则：

(1)事件与事件是什么关系？

(2)事件与事件的交事件与事件是什么关系？

【答案】(1).(2)事件与事件的交事件与事件相等.

【解析】(1)对于事件,可能的结果为1个红球和2个白球或2个红球和1个白球,故.

(2)对于事件,可能的结果为1个红球和2个白球,2个红球和1个白球或3个红球,故,所以事件与事件的交事件与事件相等.

【例2-2】(2021·全国高一)掷一枚骰子，给出下列事件：

“出现奇数点”，“出现偶数点”，“出现的点数小于3”.

求：(1)，；(2)，.

【答案】(1)，“出现2点”.

(2)“出现1，2，3，4，5或6点”，“出现1，2，4或6点”.

【解析】由题意知：“出现奇数点”，“出现偶数点”，

“出现的点数小于3”，

(1)，出现2点”；

(2)“出现1，2，3，4，5或6点”，

“出现1，2，4或6点”.

【举一反三】

1．(2020·全国高一课时练习)用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色，每个圆只涂一种颜色.设事件“三个圆的颜色全不相同”，事件“三个圆的颜色不全相同”，事件“其中两个圆的颜色相同”，事件“三个圆的颜色全相同”.

(1)写出试验的样本空间.

(2)用集合的形式表示事件.

(3)事件与事件有什么关系？事件和的交事件与事件有什么关系？并说明理由.

【答案】(1)见解析；(2)见解析；(3)事件包含事件，事件和的交事件与事件互斥.见解析

【解析】(1)由题意可知3个球可能颜色一样,可能有2个一样,另1个异色,或者三个球都异色.则试验的样本空间

{(红,红,红),(黄,黄,黄),(蓝,蓝,蓝),(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝),(红,黄,蓝)}.

(2){(红,黄,蓝)}

{(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝),(红,黄,蓝)}

{(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝)}.

{(红,红,红),(黄,黄,黄),(蓝,蓝,蓝)}.

(3)由(2)可知事件包含事件,事件和的交事件与事件互斥.

2．(2021·全国高一)记某射手一次射击训练中，射中10环、9环、8环、7环分别为事件，，，，指出下列事件的含义：

(1)；

(2)；

(3).

【答案】(1)射中10环或9环或8环.

(2)射中9环.

(3)射中10环或6环或5环或4环或3环或2环或1环或0环.

【解析】(1)=射中10环，=射中9环，=射中8环，射中10环或9环或8环.

(2)=射中8环，射中环数不是8环，则射中9环.

(3)射中9环或8环或7环，

则射中10环或6环或5环或4环或3环或2环或1环或0环.

3．(2021·全国高一)在试验“甲、乙、丙三人各射击1次，观察中靶的情况”中，事件A表示随机事件“甲中靶”，事件B表示随机事件“乙中靶”，事件C表示随机事件“丙中靶”，试用A，B，C的运算表示下列随机事件：

(1)甲未中靶；

(2)甲中靶而乙未中靶；

(3)三人中只有丙未中靶；

(4)三人中至少有一人中靶；

(5)三人中恰有两人中靶.

【答案】(1)(2)(3)(4)(5)

【解析】(1)甲未中靶：.(2)甲中靶而乙未中靶：,即.

(3)三人中只有丙未中靶：,即.

(4)三人中至少有一人中靶.

(5)三人中恰有两人中靶.

考法三  互斥与对立

【例3】(多选)(2020·全国高一课时练习)袋中有红球3个，白球2个，黑球1个，从中任取2个，则互斥的两个事件是(    )

A．至少有一个白球与都是白球

B．恰有一个红球与白、黑球各一个

C．至少一个白球与至多有一个红球

D．至少有一个红球与两个白球

【答案】BD

【解析】袋中装有红球3个、白球2个、黑球1个，从中任取2个，

在A中，至少有一个白球和都是白球两个事件能同时发生，不是互斥事件，故A不成立.

在B中，恰有一个红球和白、黑球各一个不能同时发生，是互斥事件，故B成立；

在C中，至少一个白球与至多有一个红球，能同时发生，故C不成立；

在D中，至少有一个红球与两个白球两个事件不能同时发生，是互斥事件，故D成立；

故选：BD.

【举一反三】

1．(多选)(2020·全国高一课时练习)一个人连续射击2次，则下列各事件关系中，说法正确的是(    )

A．事件“两次均击中”与事件“至少一次击中”互为对立事件

B．事件“恰有一次击中”与事件“两次均击中”互为互斥事件

C．事件“第一次击中”与事件“第二次击中”互为互斥事件

D．事件“两次均未击中”与事件“至少一次击中”互为对立事件

【答案】BD

【解析】对于A，事件“至少一次击中”包含“一次击中”和“两次均击中“，所以不是对立事件，A错误

对于B，事件“恰有一次击中”是“一次击中、一次不中”它与事件“两次均击中”是互斥事件，B正确

对于C，事件“第一次击中”包含“第一次击中、第二次击中”和“第一次击中、第二次不中”，所以与事件“第二次击中”不是互斥事件，C错误

对于D，事件“两次均未击中”的对立事件是“至少一次击中”，D正确

故选：BD

2．(多选)(2020·全国高一课时练习)下面结论正确的是(    )

A．若，则事件A与B是互为对立事件

B．若，则事件A与B是相互独立事件

C．若事件A与B是互斥事件，则A与也是互斥事件

D．若事件A与B是相互独立事件，则A与也是相互独立事件

【答案】BD

【解析】对于A选项，要使为对立事件，除还需满足，也即不能同时发生，所以A选项错误.

对于C选项，包含于，所以与不是互斥事件，所以C选项错误.

对于B选项，根据相互独立事件的知识可知，B选项正确.

对于D选项，根据相互独立事件的知识可知，D选项正确.

故选：BD

3．(2020·全国高一课时练习)在试验E“连续抛掷一枚骰子2次，观察每次掷出的点数”中，事件A表示随机事件“第一次掷出的点数为1”，事件表示随机事件“第一次掷出的点数为1，第二次掷出的点数为j，事件B表示随机事件“2次掷出的点数之和为6”，事件C表示随机事件“第二次掷出的点数比第一次的大3”，

(1)试用样本点表示事件与；

(2)试判断事件A与B，A与C，B与C是否为互斥事件；

(3)试用事件表示随机事件A.

【答案】(1)详见解析(2)事件A与事件B，事件A与事件C不是互斥事件，事件B与事件C是互斥事件.(3)

【解析】由题意可知试验E的样本空间为

,

,

,

,

,

.

(1)因为事件A表示随机事件“第一次掷出的点数为1”,所以满足条件的样本点有,即.

因为事件B表示随机事件“2次掷出的点数之和为6”,所以满足条件的样本点有,即.

所以,.

(2)因为事件C表示随机事件“第二次掷出的点数比第一次的大3”,所以.

因为,,,所以事件A与事件B,事件A与事件C不是互斥事件,事件B与事件C是互斥事件.

(3)因为事件表示随机事件“第一次掷出的点数为1,第二次掷出的点数为”,

所以,

所以.

考法四 古典概型

【例4】(2020·全国高一课时练习)在一次语文考试的阅卷过程中，两位老师对一篇作文打出的分数都是两位的正整数，且十位数字都是，则两位老师打出的分数之差的绝对值小于或等于的概率为(    )

A． B． C． D．

【答案】C

【解析】用表示两位老师的打分，则的所有可能情况有种.

当时，可取，，共种；

当，，，，，，，时，的取值均有种；

当时，可取，，共种；

综上可得两位老师打出的分数之差的绝对值小于或等于的情况有种，

由古典概型的概率公式可得所求概率故选：C.

【举一反三】

1．(2020·全国高一课时练习)从数字1，2，3，4中任取两个数，则这两个数中其中一个数为另一个数的整数倍的概率为(    )

A． B． C． D．

【答案】D

【解析】基本事件为共6个，其中符合条件的基本事件为共4个，所求概率为.故选：D

2．(2021·全国高一)把分别写有1，2，3，4的四张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么2，3连号的概率为(    )

A． B． C． D．

【答案】B

【解析】分三类情况，第一类1，2连号，则甲、乙、丙三个人拿到的卡片可能为，，，，，，有6种分法；

第二类2，3连号，则甲、乙、丙三个人拿到的卡片可能为，，，，，，有6种分法；

第三类3，4连号，则甲、乙、丙三个人拿到的卡片可能为，，，，，，有6种分法；

共有18种分法，

则2，3连号的概率为.

故选：B.

3．(2021·全国高一)为了更好了解某年入伍新兵的身高情况，解放军某部随机抽取名新兵，分别对他们的身高进行了测量，并将测量数据分为以下五组：，，，，进行整理，如下表所示：

(1)在下面的图纸中，画出频率分布直方图；

(2)若在第4，5两组中，用分层抽样的方法抽取6名新兵，再从这6名新兵中随机抽取2名新兵进行体能测试，求这2名新兵来自不同组的概率．

【答案】(1)直方图见解析；(2).

【解析】(1)频率分布直方图如下图所示：

（2）因为第4，5组共有30名新兵，所以利用分层抽样从中抽取6名，每组应抽取的人数分别为：

4组：名，第5组：名，

设第组抽取的4名新兵分别为，，，，第5组抽取的2名新兵分别为，．

从这6名新兵中随机抽取2名新兵，有以下15种情况：，，，，，，，，，，，，，，，

这2名新兵来自不同组的情况有以下8种：，，，，，，，，故所求的概率．

考法五  概率的基本性质

【例5-1】(2020·全国高一课时练习)老师讲一道数学题，李峰能听懂的概率是0.8，是指(    )

A．老师每讲一题，该题有80%的部分能听懂，20%的部分听不懂

B．老师在讲的10道题中，李峰能听懂8道

C．李峰听懂老师所讲这道题的可能性为80%

D．以上解释都不对

【答案】C

【解析】概率的意义就是事件发生的可能性大小，即李峰听懂老师所讲这道题的可能性为80%.故选：C

【例5-2】(2020·全国高一课时练习)在学校运动会开幕式上，100名学生组成一个方阵进行表演，他们按照性别(M(男)、F(女))及年级((高一)、(高二)、(高三))分类统计的人数如下表：

若从这100名学生中随机选一名学生，求下列概率：

____________，____________，____________，____________，____________，____________，____________

【答案】            0               

【解析】；

；

；

；

；

；

故答案为：(1)；(2)；(3)1；(4)0；(5)0.35；(6)0.76；(7)0.07

【举一反三】

1．(2020·全国高一课时练习)在北京消费季活动中，某商场为促销举行购物抽奖活动，规定购物消费每满200元就可以参加一次抽奖活动，中奖的概率为.那么以下理解正确的是(    )

A．某顾客抽奖10次，一定能中奖1次

B．某顾客抽奖10次，可能1次也没中奖

C．某顾客消费210元，一定不能中奖

D．某顾客消费1000元，至少能中奖1次

【答案】B

【解析】中奖概率表示每一次抽奖中奖的可能性都是，故不论抽奖多少次，都可能一次也不中奖，

故选：B.

2．(2020·全国高一课时练习)某射击运动员平时训练成绩的统计结果如下：

如果这名运动员只射击一次，以频率作为概率，求下列事件的概率；

(1)命中10环；

(2)命中的环数大于8环；

(3)命中的环数小于9环；

(4)命中的环数不超过5环.

【答案】(1)0.2  (2)0.5  (3)0.5  (4)0

【解析】用x表示命中的环数，由频率表可得.

(1)；

(2)(或)；

(3)；

(4).

3．(2021·全国高一课时练习)判断下列说法是否正确，若错误，请举出反例

(1)互斥的事件一定是对立事件，对立事件不一定是互斥事件；

(2)互斥的事件不一定是对立事件，对立事件一定是互斥事件；

(3)事件与事件B中至少有一个发生的概率一定比与B中恰有一个发生的概率大；

(4)事件与事件B同时发生的概率一定比与B中恰有一个发生的概率小.

【答案】(1)错误，举例见解析；(2)正确；(3)错误，举例见解析；(4)错误，举例见解析.

【解析】(1)错误；(2)正确；(3)错误：(4)错误.

设某试验的样本空间为.

(1)中反例，取，则A,B互斥但不对立.

(2)由互斥事件与对立事件的定义可知(2)正确

(3)中反例，取,则.

(4)中反例，取,则,.

4．(2020·全国高一课时练习)甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶概率为0.9，求下列事件的概率：

(1)两人都中靶；

(2)恰好有一人中靶；

(3)两人都脱靶；

(4)至少有一人中靶.

【答案】(1)0.72  (2)0.26  (3)0.02  (4)0.98

【解析】设“甲中靶”, “乙中靶”,则“甲脱靶”,“乙脱靶”,由于两个人射击的结果互不影响,所以A与B相互独立,A与,与B,与都相互独立

由已知可得,.

(1) “两人都中靶”,由事件独立性的定义

得

(2)“恰好有一人中靶” ,且与互斥

根据概率的加法公式和事件独立性定义,得

(3)事件“两人都脱靶”,

所以

(4)方法1：事件“至少有一人中靶”,且AB,与两两互斥,

所以

方法2：由于事件“至少有一人中靶”的对立事件是“两人都脱靶”

根据对立事件的性质,得事件“至少有一人中靶”的概率为

5．(2020·全国高一课时练习)已知n是一个三位正整数，若n的个位数字大于十位数字，十位数字大于百位数字，则称n为“三位递增数”(如135，256，345等)

现要从甲乙两名同学中，选出一个参加某市组织的数学竞赛，选取的规则如下：从由1，2，3，4，5，6组成的所有“三位递增数”中随机抽取1个数，且只抽取1次，若抽取的“三位递增数”是偶数，则甲参加数学竞赛；否则，乙参加数学竞赛.

(1)由1，2，3，4，5，6可组成多少“三位递增数”？并一一列举出来.

(2)这种选取规则对甲乙两名学生公平吗？并说明理由.

【答案】(1)见解析；(2)不公平，理由见解析.

【解析】(1)由题意知，所有由1，2，3，4，5，6组成的“三位递增数共有20个.

分别是123，124，125，126，134，135，136，145，146，156，234，235，236，245，246，256，345，346，356，456.

(2)不公平由(1)知，所有由1，2，3，4，5，6组成的“三位递增数”有20个，记“甲参加数学竟赛”为事件A，记“乙参加数学竞赛”为事件B.则事件A含有基本事件有：124，134，234，126，136，146，156，236，246，256，346，356，456共13个.

由古典概型计算公式，得

，

又A与B对立，所以，

所以.故选取规则对甲、乙两名学生不公平.