2022年中考数学二轮专题《动态几何问题》（含答案）

这是一份2022年中考数学二轮专题《动态几何问题》（含答案），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
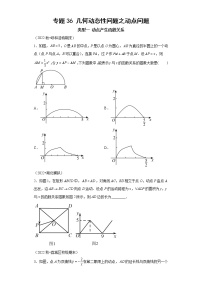
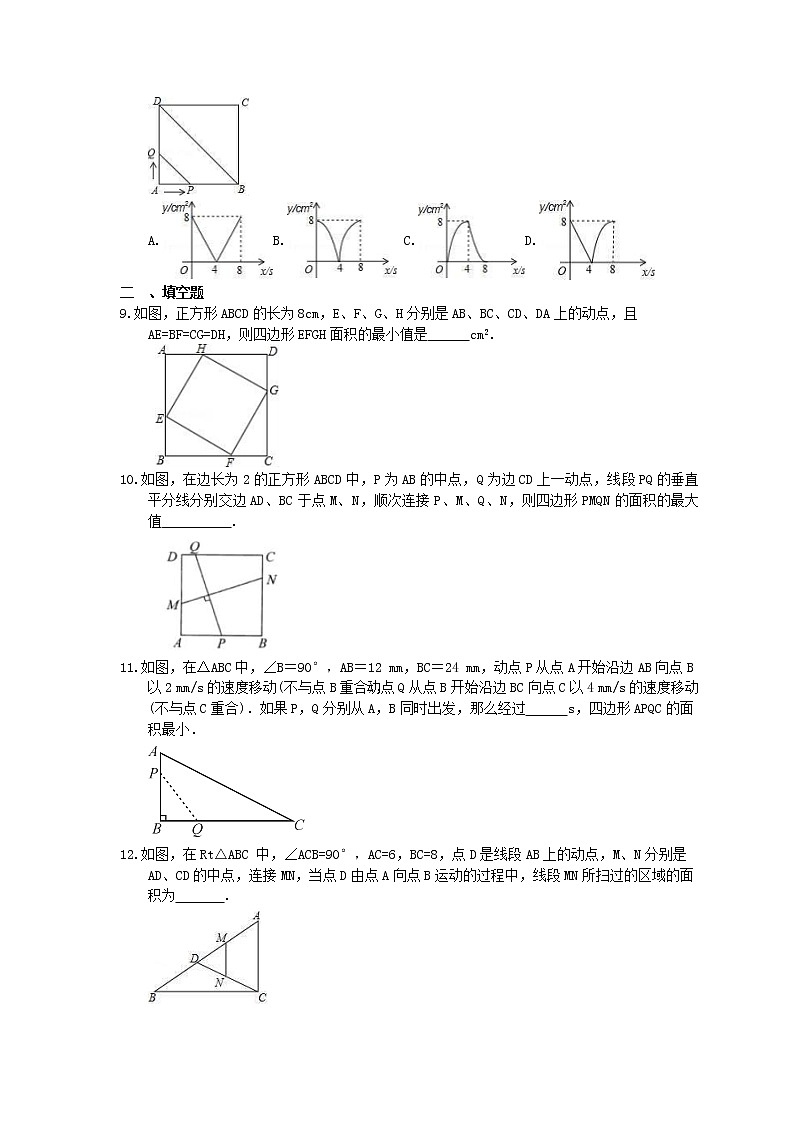
2022年中考数学二轮专题《动态几何问题》一 、选择题1.如图，正方形ABCD的边长为2 cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x(cm)，在下列图象中，能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是(      )2.如图，是一对变量满足的函数关系的图象.有下列3个不同的问题情境：①小明骑车以400米/分的速度匀速骑了5分钟，在原地休息了4分钟，然后以500米/分的速度匀速骑回出发地，设时间为x分钟，离出发地的距离为y千米；②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个桶注水，注5分钟后停止，等4分钟后，再以2升/分的速度匀速倒空桶中的水，设时间为x分钟，桶内的水量为y升；③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0，其中，符合图中所示函数关系的问题情境的个数为(　　)A.0                      B.1                          C.2                            D.33.如图，正方形ABCD的边长为4cm，动点P从点A出发，沿A→D→C的路径以每秒1cm的速度运动(点P不与点A、点C重合)，设点P运动时间为x秒，四边形ABCP的面积为ycm2，则下列图象能大致反映y与x的函数关系的是(　　)A.  B. C.   D.4.如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则当x=7时，点E应运动到(        )A.点C处        B.点D处        C.点B处        D.点A处5.如图，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△CEH的周长为定值.其中正确的结论有（  ） A.①②③                            B.①②④                 C.①③④                            D.①②③④6.如图，点A的坐标为(0，1)，点B是x轴正半轴上的一动点，以AB为边作等腰直角△ABC，使∠BAC=90°，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是(　　)A.     B.    C.   D.7.如图，在平面直角坐标系中，矩形ABCD的边BC在x轴上，点D的坐标为(﹣2，6)，点B是动点，反比例函数y=(x＜0)经过点D，若AC的延长线交y轴于点E，连接BE，则△BCE的面积为(　　)A.3       B.5       C.6       D.78.如图，正方形ABCD的边长为4cm，动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动，设运动时间为x(单位：s)，四边形PBDQ的面积为y(单位：cm2)，则y与x(0≤x≤8)之间函数关系可以用图象表示为(　　)A.B. C.D.二 、填空题9.如图，正方形ABCD的长为8cm，E、F、G、H分别是AB、BC、CD、DA上的动点，且AE=BF=CG=DH，则四边形EFGH面积的最小值是      cm2． 10.如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，线段PQ的垂直平分线分别交边AD、BC于点M、N，顺次连接P、M、Q、N，则四边形PMQN的面积的最大值          . 11.如图，在△ABC中，∠B＝90°，AB＝12 mm，BC＝24 mm，动点P从点A开始沿边AB向点B以2 mm/s的速度移动(不与点B重合)，动点Q从点B开始沿边BC向点C以4 mm/s的速度移动(不与点C重合)．如果P，Q分别从A，B同时出发，那么经过      s，四边形APQC的面积最小．12.如图，在Rt△ABC 中，∠ACB=90°，AC=6，BC=8，点D是线段AB上的动点，M、N分别是AD、CD的中点，连接MN，当点D由点A向点B运动的过程中，线段MN所扫过的区域的面积为　   　.13.如图，已知动点A在函数y=(x＞0)的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点P，Q，当QE：DP=9：25时，图中的阴影部分的面积等于　   　.14.如图，在Rt△ABC中，∠BAC=90°，AB=AC=16 cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t s(0<t<8)，则t=________时，S1=2S2.三 、解答题15.如图，⊙O的直径AB=4，点C为⊙O上的一个动点，连接OC，过点A作⊙O的切线，与BC的延长线交于点D，点E为AD的中点，连接CE.(1)求证：CE是⊙O的切线；(2)填空：①当CE=　　　　　时，四边形AOCE为正方形；②当CE=　　　　　时，△CDE为等边三角形.16.如图，在矩形ABCD中，AB=3，BC=4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E.F，点P是边DC上的一个动点，且保持DP=AE，连接PE.PF，设AE=x(0＜x＜3).(1)填空：PC=_____，FC=_________；(用含x的代数式表示)(2)求△PEF面积的最小值；(3)在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由.17.如图，在平面直角坐标系中，面积为4的正方形OABC的顶点O与坐标原点重合，边OA、OC分别在x轴、y轴的正半轴上，点B、P都在函数y=(x＞0)的图象上，过动点P分别作轴x、y轴的平行线，交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S，点P的横坐标为m.(1)求k的值；(2)用含m的代数式表示CD的长；(3)求S与m之间的函数关系式.18.如图，在四边形ABCD中，AD∥BC，AD=2，AB=2，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F.(1)求∠ABE的大小及的长度；(2)在BE的延长线上取一点G，使得上的一个动点P到点G的最短距离为2－2，求BG的长.
0.答案解析1.答案为：A.2.答案为：C3.答案为：D.4.B5.答案为：D；6.答案为：A.7.答案为：C.8.答案为：B.9.答案为：32．10.答案为：2.5；11.答案为：3.12.答案为：12.13.答案为：.14.答案为：6.15. (1)证明：如图，连接AC、OE.∵AD为⊙O的切线，∴∠OAE=90°.∵AB为⊙O的直径，∴∠ACB=90°，∴△ACD是直角三角形.∵点E是AD的中点，∴EA=EC.又OA=OC，OE=OE，∴△OCE≌△OAE，∴∠OAE=∠OCE=90°，即OC⊥CE，∴CE是⊙O的切线.(2)① 2;②.16.解：(1)∵四边形ABCD是矩形[w~ww.zz#st^ep%.@com]∴AD∥BC，DC=AB=3，AO=CO∴∠DAC=∠ACB，且AO=CO，∠AOE=∠COF∴△AEO≌△CFO(ASA)∴AE=CF∵AE=x，且DP=AE∴DP=x，CF=x，DE=4﹣x，∴PC=CD﹣DP=3﹣x故答案为：3﹣x，x(2)∵S△EFP=S梯形EDCF﹣S△DEP﹣S△CFP，∴S△EFP=﹣﹣×x×(3﹣x)=x2﹣x+6=(x﹣)2+[来源:^*中&%教网@]∴当x=时，△PEF面积的最小值为(3)不成立理由如下：若PE⊥PF，则∠EPD+∠FPC=90°又∵∠EPD+∠DEP=90°∴∠DEP=∠FPC，且CF=DP=AE，∠EDP=∠PCF=90°∴△DPE≌△CFP(AAS)∴DE=CP∴3﹣x=4﹣x则方程无解，∴不存在x的值使PE⊥PF，即PE⊥PF不成立.17.解(1)∵正方形OABC的面积4，∴BA=BC=OA=OC=2.∴点 B(2，2)∵点B、P都在函数y=(x＞0)的图象上∴k=2×2=4∴解析式y=(2)∵点P在y=的图象上，且横坐标为m，∴当0＜m≤2时，CD=﹣2当m＞2时，CD=2﹣(3)当0＜m≤2时，S=2m当m＞2时，S=2×=18.解：（1）连接AE，如图，∵以AD为半径的圆与BC相切于点E，∴AE⊥BC，AE=AD=2.在Rt△AEB中，AE=2，AB=2，∴BE=2，即△ABE是等腰直角三角形，∴∠ABE=45°.∵AD∥BC，∴∠DAB＋∠ABE=180°，∴∠DAB=135°，∴的长度为=；（2）如图，根据两点之间线段最短，可得当A，P，G三点共线时PG最短，此时AG=AP＋PG=2＋2－2=2，∴AG=AB.∵AE⊥BG，∴BE=EG.∴BG=2BE=4.