2022年全国各地自招数学好题汇编之专题20 平面向量（word版含答案）

这是一份2022年全国各地自招数学好题汇编之专题20 平面向量（word版含答案），共20页。试卷主要包含了定义等内容，欢迎下载使用。
专题20 平面向量
一．选择题（共1小题）
1．（2018秋•松江区期中）已知，是两个非零向量，是一个单位向量，下列等式中正确的是（　　）
A．＝ B．＝ C．||＝ D．||＝
二．填空题（共5小题）
2．（2021•宝山区校级自主招生）已知△ABC，＝，＝，边BC上有点P1、P2、P3…P22，使得BP1＝P1P2＝P2P3＝…P22C，则+++…+＝　 　．
3．（2016•宝山区校级自主招生）在△ABC中，设，，P是中线AE与中线CF的交点，则＝　 　．（用表示）
4．（2014•宝山区校级自主招生）如图，在△ABC中，D、E分别为AC、AB的中点，＝a，＝b，则＝　 　．

5．（2021春•虹口区校级期末）如图，平面内有三个非零向量、、，它们的模都相等，并且两两的夹角均为120度，则++＝　 　．

6．已知四边形ABCD的对角线AC，BD互相垂直，点E、F分别是AB、CD中点．若＝、则＝　 　（用向量、表示）；若||＝4，||＝3，则||＝　 　．
三．解答题（共13小题）
7．（2019•湖北自主招生）定义：在平面内，我们把既有大小又有方向的量叫做平面向量．平面向量可以用有向线段表示，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向．其中大小相等，方向相同的向量叫做相等向量．
如以正方形ABCD的四个顶点中某一点为起点，另一个顶点为终点作向量，可以作出8个不同的向量：、、、、、、、（由于和是相等向量，因此只算一个）．

（1）作两个相邻的正方形（如图一）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2），试求f（2）的值；
（2）作n个相邻的正方形（如图二）“一字型”排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（n），试求f（n）的值；
（3）作2×3个相邻的正方形（如图三）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2×3），试求f（2×3）的值；
（4）作m×n个相邻的正方形（如图四）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（m×n），试求f（m×n）的值．
8．（2011•瓯海区校级自主招生）先阅读短文，再解答短文后面的问题．
在几何学中，通常用点表示位置，用线段的长度表示两点间的距离，用一条射线表示一个方向．在平面内，从一点出发的所有射线，可以用来表示平面内的各个不同的方向．
在线段的两个端点中，我们规定一个顺序：A为始点，B为终点，我们就说线段AB具有射线AB的方向．具有方向的线段，叫做有向线段．通常在有向线段的终点处画上箭头表示它的方向．以A为始点，以B为终点的有向线段记作．应注意，始点一定要写在终点的前面．
已知有向线段，线段AB的长度叫做有向线的长度（或模），的长度记作||．有向线段包含三个要素：始点、方向和长度．知道了有向线段的始点，它的终点就被方向和长度所唯一确定．
解答下列问题：
（1）如果两条有向线段的长度相同，始点的位置相同，那么它们的终点位置是否相同？为什么？
（2）如果两条有向线段的方向相同，始点的位置相同，那么它们的终点位置是否相同？为什么？
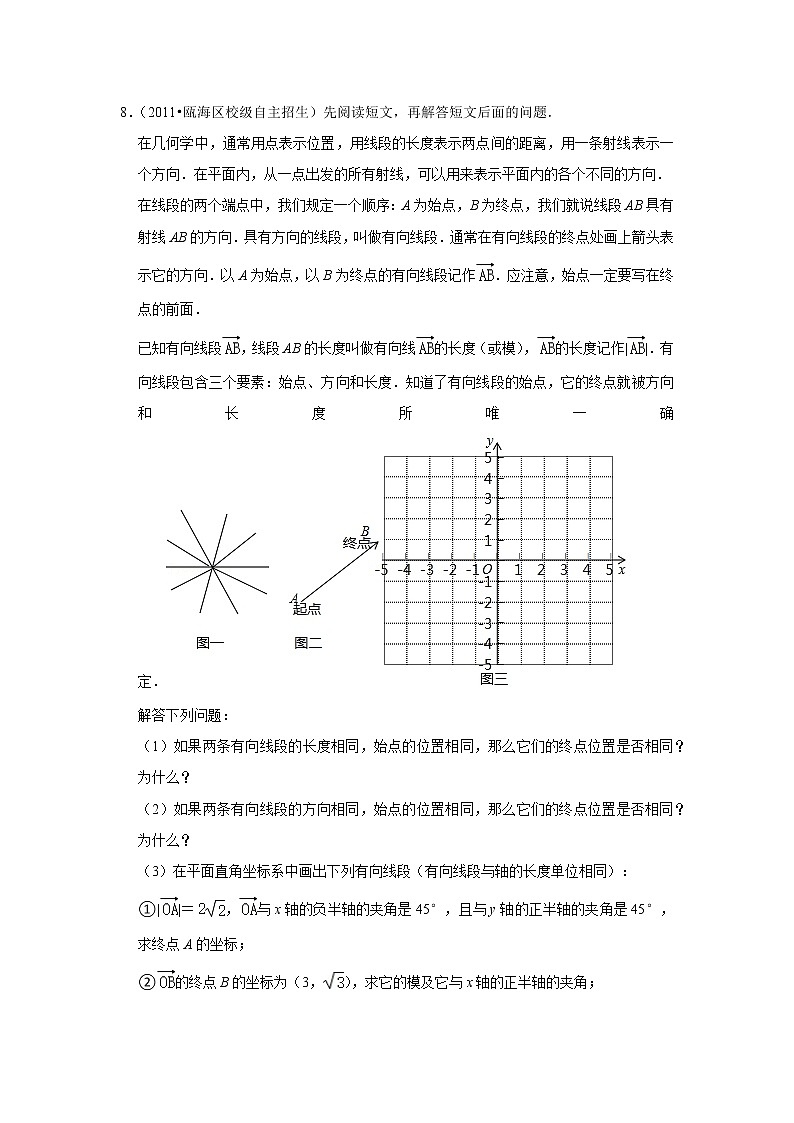
（3）在平面直角坐标系中画出下列有向线段（有向线段与轴的长度单位相同）：
①||＝，与x轴的负半轴的夹角是45°，且与y轴的正半轴的夹角是45°，求终点A的坐标；
②的终点B的坐标为（3，），求它的模及它与x轴的正半轴的夹角；
（4）已知点M、A、P在同一直线上；那么一定成立吗？请在图中画出图形并加以说明．
9．（2011•长沙校级自主招生）定义：在平面内，我们把既有大小又有方向的量叫做平面向量．平面向量可以用有向线段表示，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向．其中大小相等，方向相同的向量叫做相等向量．
如以正方形ABCD的四个顶点中某一点为起点，另一个顶点为终点作向量，可以作出8个不同的向量：、、、、、、、（由于和是相等向量，因此只算一个）．
（1）作两个相邻的正方形（如图一）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2），试求f（2）的值；

（2）作n个相邻的正方形（如图二）“一字型”排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（n），试求f（n）的值；

（3）作2×3个相邻的正方形（如图三）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2×3），试求f（2×3）的值；

（4）作m×n个相邻的正方形（如图四）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（m×n），试求f（m×n）的值．

10．（2021春•黄浦区期末）如图，点E在平行四边形ABCD的对角线BD的延长线上．
（1）填空：+＝　 　.﹣＝　 　；
（2）求作：+（不写作法，保留作图痕迹，写出结果）

11．（2018春•黄浦区期末）如图，已知点E在平行四边形ABCD的边AB上，设＝，＝，＝，再用图中的线段作向量，
（1）写出与平行的向量　 　．
（2）试用向量、、表示向量、.＝　 　；＝　 　．
（3）求作．

12．（2018春•浦东新区期末）已知：如图，在平行四边形ABCD中，E、F分别是对角线BD上的两点，且BE＝DF，＝，＝，＝．
（1）用向量、、表示下列向量：向量＝　 　，向量＝　 　，向量＝　 　；
（2）求作：+．

13．（2017秋•铜梁区期末）我们规定：若＝（a，b），＝（c，d），则*＝ac+bd，如＝（2，3），＝（4，5），则*＝2×4+3×5＝23．
（1）设＝（x2，﹣4），＝（﹣2，x﹣1），且•＝﹣26，求实数x的值．
（2）设＝（x﹣a，1），＝（x﹣a，x+2），且关于x的函数y＝*的图象与一次函数y＝2x+3的图象有两个不相同的交点，求a的取值范围．
14．（2017秋•海安市校级月考）我们规定：若＝（a，b），＝（c，d），则＝ac+bd．如＝（1，2），
＝（3，5），则＝1×3+2×5＝13．
（1）已知＝（2，4），＝（2，﹣3），求；
（2）已知＝（x+2，1），＝（x﹣2，3x﹣1）．
①求y＝．
②判断y1＝的函数图象与一次函数y2＝x+3的图象是否有公共点，若有，请求出公共点的坐标，若没有，请说明理由．
③直接写出当y1≥y2时，x的取值范围．
15．（2016•闸北区一模）如图，已知平行四边形ABCD的对角线相交于点O，点E是边BC的中点，联结DE交AC于点G．设＝，＝，
（1）试用、表示向量；
（2）试用、表示向量．

16．（2015秋•闵行区期末）如图，已知四边形ABCD，点P、Q、R分别是对角线AC、BD和边AB的中点，设＝，＝．
（1）试用，的线性组合表示向量；（需写出必要的说理过程）
（2）画出向量分别在，方向上的分向量．

17．（2013•闸北区一模）已知：如图，在平行四边形ABCD中，对角线AC、BD相交于点O，点M、N分别在边AO和边OD上，且AM＝AO，ON＝OD，设＝，＝，试用、的线性组合表示向量和向量．

18．（2010秋•长宁区期末）如图，在边长为l的小正方体组成的网格中，小正方体的顶点称为格点，△ABC的三个顶点都在格点上．
（1）在网格中确定一点D，使得＝（只要画出向量，不必写作法）；
（2）若E为BC的中点，则tan∠CAE＝　 　；
（3）在△ACD中，求∠CAD的正弦值．

19．（2017秋•虹口区校级月考）如图，已知点M是△ABC边BC上一点，设＝，＝．
（1）当＝2时，＝　 　；（用与表示）
（2）当＝+时，＝　 　；
（3）在原图上作出在、上的分向量．

专题20 平面向量
一．选择题（共1小题）
1．【解答】解：A、得出的是a的方向不是单位向量，故错误；
B、左边得出的是a的方向，右边得出的是b的方向，两者方向不一定相同，故错误；
C、由于单位向量只限制长度，不确定方向，故错误；
D、符合向量的长度及方向，故正确；
故选：D．
二．填空题（共5小题）
2．【解答】解：如图，设＝，
则有++•••+＝（+）+（+2）+•••+（+22）
＝22+23×11，
∵+23＝，
∴++•••+＝11+11+23×11＝11+11（+23）＝11+11，
故答案为：11+11．



3．【解答】解：∵，AE是△ABC的中线，
∴＝＝﹣＝﹣，
∵，
∴＝+＝﹣+，
∵P是中线AE与中线CF的交点，
∴＝＝（﹣+）＝﹣，
∴＝+＝﹣+﹣＝﹣．
故答案为：﹣．

4．【解答】解：连接DE，
∵＝，＝，
∵D为AC的中点，
∴＝＝，
∴＝﹣＝﹣，
∵在△ABC中，D、E分别为AC、AB的中点，
∴DE∥BC，
∴△PED∽△PCB，
∴DP：PB＝DE：BC＝1：2，
∴＝＝（﹣）＝﹣．
故答案为：﹣．

5．【解答】解：延长AO到T，使得OT＝OA，连接TB．

∵＝，
∴+＝+＝，
∵OB＝OT，∠BOT＝60°，
∴△OBT是等边三角形，
∴∠T＝∠TOC＝60°，
∴BT∥OC，BT＝OC，
∴+＝，
∴++＝，
故答案为：．
6．【解答】解：①取AD的中点G，连接EG、GF．

∵AE＝EB，AG＝GD，
∴GE∥BD，GE＝DB，
∴＝，
同法可得：＝，
∵＝+＝﹣，
②∵||＝4，||＝3，
∴AC＝4，BD＝3，
∵GE＝，EG＝2，
∵EG∥BD，FG∥AC，AC⊥BD，
∴EG⊥FG，
∴∠EGF＝90°，
∴EF＝＝，
∴||＝，
故答案为﹣，．
三．解答题（共13小题）
7．【解答】解：（1）作两个相邻的正方形，以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数f（2）＝14；

（2）分别求出作两个、三个、四个相邻的正方形（如图1）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同的向量个数，找出规律，
∵f（1）＝6×1+2＝8，f（2）＝6×2+2＝14，f（3）＝6×3+2＝20，f（4）＝6×4+2＝26，
∴f（n）＝6n+2；

（3）f（2×3）＝34；

（4）∵f（2×2）＝24，f（2×3）＝34，f（2×4）＝44，f（3×2）＝34，f（3×3）＝48，f（3×4）＝62
∴f（m×n）＝2（m+n）+4mn．
8．【解答】解：（1）它们的终点位置不一定相同．
∵有向线段包含三个要素：始点、方向和长度，知道两条有向线段的长度相同，始点的位置相同，但不知道它们的方向是否相同，
∴它们的终点位置不一定相同；

（2）它们的终点位置不一定相同．
∵有向线段包含三个要素：始点、方向和长度，知道两条有向线段的方向相同，始点的位置相同，但不知道它们的长度是否相同，
∴它们的终点位置不一定相同；

（3）①如图：∵确与x轴的负半轴的夹角是45°，且与y轴的正半轴的夹角是45°，
∴点A位于第二象限，
∴点A的横坐标为：﹣2•cos45°＝﹣2，点A的纵坐标为：2•sin45°＝2．
∴点A的坐标为（﹣2，2）；

②∵的终点B的坐标为（3，），
∴OC＝3，BC＝，
∴tan∠BOC＝＝，
∴∠BOC＝30°，
∴||＝＝2；
∴它的模及为2，与x轴的正半轴的夹角为30°；

（4）若M、A、P在同一直线上，不一定成立．
如图甲：成立，
如图乙：不成立．
∴若M、A、P在同一直线上，不一定成立．


9．【解答】解：（1）作两个相邻的正方形，以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数f（2）＝14；

（2）分别求出作两个、三个、四个相邻的正方形（如图1）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同的向量个数，找出规律，
∵f（1）＝6×1+2＝8，f（2）＝6×2+2＝14，f（3）＝6×3+2＝20，f（4）＝6×4+2＝26，
∴f（n）＝6n+2；

（3）f（2×3）＝34；

（4）∵f（2×2）＝24，f（2×3）＝34，f（2×4）＝44，f（3×2）＝34，f（3×3）＝48，f（3×4）＝62
∴f（m×n）＝2（m+n）+4mn．
10．【解答】解：（1）+＝，
∵＝，
∴﹣＝﹣＝；
故答案为：；．

（2）如图，即为所求+．

11．【解答】解：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，
∴与平行的向量有：、和．
故答案是：、和．

（2）＝﹣＝﹣，即；
＝﹣＝﹣+，即．
故答案是：﹣，﹣+；


（3）∵，
∴为所求作向量．

12．【解答】解：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠ADF＝∠CBE，
∵DF＝BE，
∴△ADF≌△CBE，
∴∠AFD＝∠CEB，AF＝CE，
∴∠AFB＝∠CED，
∴AF∥CE，
∴＝﹣＝﹣＝﹣，
＝+＝﹣，
＝+＝﹣，
故答案为﹣，﹣，﹣．

（2）延长EC到K，使得CK＝EC，连接BK，则向量即为所求；

13．【解答】解：（1）∵＝（x2，﹣4），＝（﹣2，x﹣1），且•＝﹣26，
∴﹣2x2﹣4（x﹣1）＝﹣26，
∴x1＝﹣5，x2＝3，

（2）由题意：y＝（x﹣a）2+x+2，
由，
消去y得到，x2﹣（2a+1）x+a2﹣1＝0，
∵关于x的函数y＝*的图象与一次函数y＝2x+3的图象有两个不相同的交点，
∴Δ＞0，
∴[﹣（2a+1）]2﹣4×1×（a2﹣1）＞0，
∴a＞﹣．
14．【解答】解：（1）＝2×2+4×（﹣3）＝﹣8；

（2）①y＝（x+2）（x﹣2）+1×（3x﹣1）＝x2+3x﹣5；
②依题意得：，
解得，，
所以y1＝的函数图象与一次函数y2＝x+3的图象有公共点，公共点的坐标为（﹣4，﹣1），（2，5）；
③如图所示，当y1≥y2时，x≤﹣4或x≥2．

15．【解答】解：（1）∵＝，＝，
∴＝+＝+，
∵四边形ABCD是平行四边形，
∴＝＝（+）＝+；

（2）∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴△ADG∽△CEG，
∴AG：CG＝AD：CE，
∵点E是边BC的中点，
∴AD：CE＝2：1，
∴AG：CG＝2：1，
∴AG：AC＝2：3，
∴＝＝+，
∴＝﹣＝+﹣＝﹣．
16．【解答】解：（1）∵点P、Q、R分别是对角线AC、BD和边AB的中点，
∴＝＝﹣，＝＝，
∴＝+＝﹣+；

（2）如图：与即为所求．

17．【解答】解：根据平行四边形法则，＝+＝+，
∵平行四边形ABCD，
∴AO＝AC，
∴＝＝（+），
∵AM＝AO，
∴OM＝AO，
∴＝﹣，
∴＝﹣×（+）＝﹣﹣；

∵AM＝AO，ON＝OD，
∴＝＝，
∴MN∥AD，
∴＝＝，
∴＝，
又∵平行四边形ABCD，
∴＝＝，
∴＝．
18．【解答】解：（1）如图：点D即为所求；


（2）如图：根据题意可知：
tan∠CAE＝＝．
故答案为：；

（3）根据题意得：AC＝＝，DC＝，AD＝，
∴△ACD不是直角三角形，
作DM⊥AC于M，
S△ADC＝S梯形AFNC﹣S△AFD﹣S△CND，
＝（AF+CN）•FN﹣AF•DF﹣DN•CN，
＝×（4+2）×5﹣×4×4﹣×2×1，
＝6，
S△ADC＝•AC•DM＝××DM＝6，
∴DM＝，
在Rt△ADM中，sin∠CAD＝＝÷＝．

19．【解答】解：（1）∵＝+＝﹣，
∵BM：CM＝2，
∴＝（﹣），
∴＝+＝+﹣＝+．
故答案为+．

（2）∵＝+＝+，
∴＝（﹣）＝，
∴BM：BC＝3：7，
∴BM：MC＝3：4，
故答案为．

（3）如图所示：在、上的分向量分别为，．

声明：试题解析著作权属所有，未经书面同意，不得复制发布