高教版（中职）基础模块上册1.3.2 并集集体备课ppt课件

这是一份高教版（中职）基础模块上册1.3.2 并集集体备课ppt课件

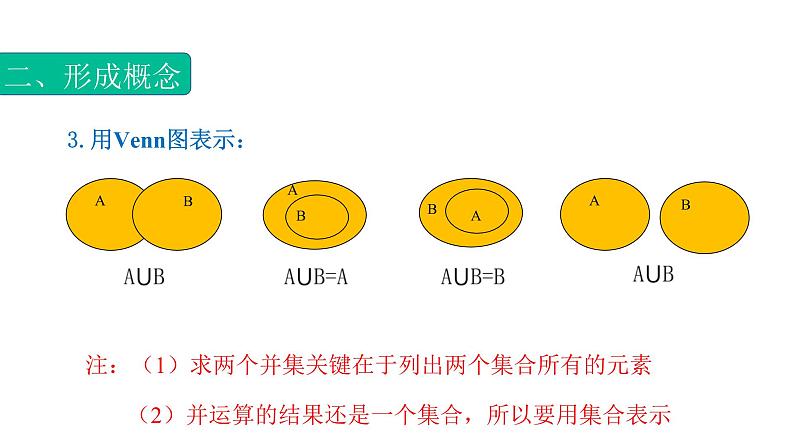
1.3.2集合的运算（并集）Set operation (Union)一、情景引入[情景1]2020新冠席卷全球，新冠感染者者甲去过的地方构成集合A={学校、餐厅、超市、体育馆}，新冠感染者乙去过的地方构成集合B={电影院，超市，学校，广场}，则高风险地区构成集合C？[提示]C={学校、餐厅、超市、体育馆、电影院、广场｝问题1：集合A、B、C是什么样的关系？A={学校、餐厅、超市、体育馆}B={电影院，超市，学校，广场}C={学校、餐厅、超市、体育馆、电影院、广场｝[提示] 集合C中的元素是由集合A、B的所有元素所组成的，这时，将C称作是A与B的并集．一、情景引入二、形成概念1.并集： 2.符号表示： （读作“A并B”）  3.用Venn图表示：注：（1）求两个并集关键在于列出两个集合所有的元素 （2）并运算的结果还是一个集合，所以要用集合表示二、形成概念    4.并集的性质： 请画图验证二、形成概念三、例题精讲例1 已知集合A，B，求A∪B．(1) A={1,2}，B={2,3}；(2) A={a , b}，B={c, d , e , f }；(3) A={1,3,5}，B= ；(4) A={2,4}，B={1,2,3,4}．解: (1) A∪B={1,2}∪{2,3}={1,2,3};(2) A∪B={a , b}∪{c , d , e , f }={a , b, c , d , e, f }; (3) 因为是不含任何元素的空集，所以A∪B={1,3,5}∪={1,3,5};(4) 集合A是集合B的真子集，A∪B={1,2,3,4}= B．【分析】 因为A∪B是由集合A和集合B的所有元素组成，当集合都是用列举法表示时，通过列举这两个集合的元素，可以得到并集，注意相同的元素只列举一次. 三、例题精讲  三、例题精讲   【点睛】对于不等式集合要用数轴来理解并集含义三、例题精讲问题2：集合的并集和交集有什么区别？（含义和符号） 思考探究问题3：在进行集合的并运算和交运算时各自的特点是什么？[提示]交运算是寻找两个集合都有的公共部分，并运算是将两个集合所有的元素进行合并．问题4：集合用列举法和描述法表示时进行运算需要注意的问题是什么？[提示]列举法求解时要不重不漏，描述法求解时要利用好数轴并注意端点的处理．思考探究四、巩固提高 【答案】D【分析】可画出Venn图或者数轴【详解】  四、巩固提高  四、巩固提高五、小结1.并集的概念及运算2.并集的描述法表示六、作业(1)读书部分： 教材章节1.3；(2)书面作业： 学习与训练1.3；谢谢Thank you