2020-2021学年河南省商丘市某校初二（下）期中考试数学试卷新人教版

这是一份2020-2021学年河南省商丘市某校初二（下）期中考试数学试卷新人教版，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

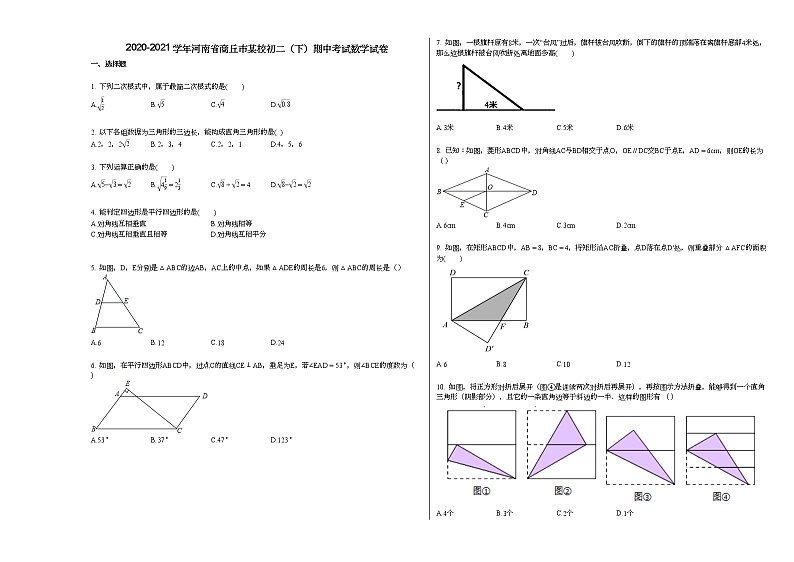
1. 下列二次根式中，属于最简二次根式的是( )
A.12B.5C.4D.0.8

2. 以下各组数据为三角形的三边长，能构成直角三角形的是( )
A.2，2，22B.2，3，4C.2，2，1D.4，5，6

3. 下列运算正确的是( )
A.5−3=2B.419=213C.8÷2=4D.8−2=2

4. 能判定四边形是平行四边形的是( )
A.对角线互相垂直B.对角线相等
C.对角线互相垂直且相等D.对角线互相平分

5. 如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的周长是6，则△ABC的周长是（ ）

A.6B.12C.18D.24

6. 如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53∘，则∠BCE的度数为（ ）

A.53∘B.37∘C.47∘D.123∘

7. 如图，一根旗杆原有8米，一次“台风”过后，旗杆被台风吹断，倒下的旗杆的顶端落在离旗杆底部4米处，那么这根旗杆被台风吹断处离地面多高( )

A.3米B.4米C.5米D.6米

8. 已知：如图，菱形ABCD中，对角线AC与BD相交于点O，OE // DC交BC于点E，AD=6cm，则OE的长为（ ）

A.6cmB.4cmC.3cmD.2cm

9. 如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为( )

A.6B.8C.10D.12

10. 如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有 （ ）

A.4个B.3个C.2个D.1个
二、填空题

命题“对顶角相等”的逆命题是________，这个逆命题是________命题．

若直角三角形的两直角边的长分别为a、b，且满足a−3+(b−4)2=0，则该直角三角形的斜边长为________．

对于任意不相等的两个数a，b，定义一种运算※如下：a※b=a+ba−b，如3※2=3+23−2=5．那么12※4=________．

如图，▱ABCD绕点A逆时针旋转45∘，得到▱ AB′C′D′（点B′与B是对应点，点C′与点C是对应点，点D′与点D是对应点）．点B′恰好落在BC边上，则∠C=________．


如图，平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点B的坐标为(10, 6)，点P为BC边上的动点，当△POA为等腰三角形时，点P的坐标为________．

三、解答题

计算：
(1)48÷3−12×12+24；

(2)24×13−4×18×1−20.

解答下列各题
(1)已知x=3+1，y=3−1，求式子x2+y2−xy的值；

(2)a，b分别是4−5的整数部分和小数部分，求式子3b+5ab的值.

如图，在平行四边形ABCD中，E，F分别在AD，BC边上，且AE=CF．
求证：
1△ABE≅△CDF；

2四边形BFDE是平行四边形．

如图，正方形网格中的每个小正方形边长都是1．
1如图1，在4×4的方格中，画一个三角形，使它的三边长都是有理数，且顶点都在格点上；

2如图2, 直接写出：
①△ABC的周长为________；②△ABC的面积为_________；③AB边上的高为________．

如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．

(1)求证：AE=CF；

(2)若∠ABE=55∘，求∠EGC的大小．

如图所示，一架长为2.5米的梯子AB斜靠在竖直的墙AC上，这时梯子底部B到墙AC的距离为0.7米.

(1)如果梯子的顶端A沿墙下滑0.4米到D，求梯子底部B向外移动的距离BE？

(2)如果梯子底部B向外移动的距离BE为1.7米，那么顶部A下滑的距离AD是否与BE相等？请给予说明.

【知识链接】
(1)有理化因式：两个含有根式的非零代数式相乘，如果它们的积不含有根式，那么这两个代数式相互叫做有理化因式．
例如：2的有理化因式是2；1−x2+2的有理化因式是1+x2+2；
(2)分母有理化：分母有理化又称“有理化分母”，也就是把分母中的根号化去．指的是如果代数式中分母有根号，那么通常将分子、分母同乘分母的有理化因式，达到化去分母中根号的目的．如：11+2=1×2−12+12−1=2−1，13+2=1×3−23+23−2=3−2．
【知识理解】
(1)填空：2x的有理化因式是________；

(2)直接写出下列各式分母有理化的结果：
①17+6=________；②132+17=________．

【启发运用】
(3)计算：11+2+13+2+12+3+⋯+1n+1+n .

如图所示，正方形ABCD的边长为4，点P为对角线BD上一动点，点E在射线BC上．

(1)填空：∠PBC=________度；

(2)若点E为BC的中点，连接PE、PC，求PE+PC的最小值；

(3)若点E是直线AP与射线BC的交点，当△PCE为等腰三角形时，求∠PEC的度数．
参考答案与试题解析
2020-2021学年河南省商丘市某校初二（下）期中考试数学试卷
一、选择题
1.
【答案】
B
【考点】
最简二次根式
【解析】
直接利用最简二次根式的概念：(1)被开方数不含分母；(2)被开方数中不含能开得尽方的因数或因式．我们把满足上述两个条件的二次根式，叫做最简二次根式，进而得出答案．
【解答】
解：A，12=22，不是最简二次根式，故此选项错误；
B，5是最简二次根式，故此选项正确；
C，4=2，不是最简二次根式，故此选项错误；
D，0.8=45，不是最简二次根式，故此选项错误．
故选B．
2.
【答案】
A
【考点】
勾股定理的逆定理
勾股数
【解析】
欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
【解答】
解：因为22+22=222=8，能构成直角三角形，故正确；
根据22+32=4+9=13，42=16，即22+32≠42，所以不能构成直角三角形，故不正确；
根据22=4，12=1，可得1+4≠4，不能构成直角三角形，故不正确；
根据42+52≠62，可知不能构成直角三角形，故不正确．
故选A．
3.
【答案】
D
【考点】
二次根式的性质与化简
二次根式的减法
二次根式的除法
【解析】
根据合并同类二次根式对A、D进行判断；根据二次根式的定义对C进行判断；根据二次根式的化简对B进行判断．
【解答】
解：A，5与2不是同类二次根式，不能合并，所以A选项错误；
B，419=379=373，所以B选项错误；
C，8÷2=22÷2=2，所以C选项错误；
D，8−2=22−2=2，所以D选项正确．
故选D．
4.
【答案】
D
【考点】
平行四边形的判定
【解析】
根据平行四边形的判定定理可知，对角线相互平分的四边形为平行四边形．
【解答】
解：根据平行四边形的判定，D能判定四边形是平行四边形．
故选D.
5.
【答案】
B
【考点】
三角形中位线定理
【解析】
本题考查的是三角形的中点的性质和三角形中位线定理，三角形的中位线平行于第三边，并且等于第三边的一半．
【解答】
解：∵ 点D、E分别是边AB，AC的中点，
∴ DE是三角形ABC的中位线，AB=2AD，AC=2AE，
∴ DE // BC，且DE=12BC，
又∵ AB=2AD，AC=2AE，
∴ AB+BC+AC=2(AD+AE+DE)，
即△ABC的周长是△DAE的周长的2倍，
∵ △DAE的周长是6，
∴ △ABC的周长是：6×2=12．
故选B.
6.
【答案】
B
【考点】
平行四边形的性质
三角形内角和定理
【解析】
由平行四边形的性质得出∠B＝∠EAD＝53∘，由角的互余关系得出∠BCE＝90∘−∠B即可．
【解答】
解：∵ 四边形ABCD是平行四边形，
∴ AD // BC，
∴ ∠B=∠EAD=53∘，
∵ CE⊥AB，
∴ ∠BCE=90∘−∠B=37∘.
故选B.
7.
【答案】
A
【考点】
勾股定理的应用
【解析】
此题暂无解析
【解答】
解：设旗杆未折断部分长为x米，则折断部分的长为(8−x)m，
根据勾股定理得：x2+42=(8−x)2，
可得：x=3m，
即距离地面3米处断裂．
故选A.
8.
【答案】
C
【考点】
菱形的性质
三角形中位线定理
【解析】
由菱形ABCD中，OE // DC，可得OE是△BCD的中位线，又由AD=6cm，根据菱形的性质，可得CD=6cm，再利用三角形中位线的性质，即可求得答案．
【解答】
解：∵ 四边形ABCD是菱形，
∴ CD=AD=6cm，OB=OD，
∵ OE // DC，O为BD的中点，
∴ OE是△BCD的中位线，
∴ OE=12CD=3cm．
故选C.
9.
【答案】
C
【考点】
翻折变换（折叠问题）
全等三角形的性质与判定
三角形的面积
勾股定理
【解析】
因为BC为AF边上的高，要求△AFC的面积，求得AF即可，求证△AFD′≅△CFB，得BF=D′F，设D′F=x，则在Rt△AFD′中，根据勾股定理求x，于是得到AF=AB−BF，即可得到结果．
【解答】
解：由于
∠AFD′=∠CFB，∠D′=∠B，AD′=BC，
易证△AFD′≅△CFB(AAS)，
∴ D′F=BF，
设D′F=x，则AF=8−x，
在Rt△AFD′中，
(8−x)2=x2+42，
解之得：x=3，
∴ AF=AB−FB=8−3=5，
∴ S△AFC=12⋅AF⋅BC=10．
故选C．
10.
【答案】
C
【考点】
翻折变换（折叠问题）
含30度角的直角三角形
【解析】
根据含30∘角所对的直角边等于斜边一半，然后依次判断直角三角形中能否找到一个角等于30∘，从而判断出答案．
【解答】
解：设正方形的边长为a，
在图①中，CE=ED=14a，BC=DB=a，
故∠EBC=∠EBD≠30∘，故△ECB不能满足它的一条直角边等于斜边的一半．
在图②中，BC=12a，AC=AE=a，
故∠BAC=30∘，从而可得∠CAD=∠EAD=30∘，
故能满足它的一条直角边等于斜边的一半．
在图③中，AC=12a，AB=a，
故∠ABC=∠DBC≠30∘，故不能满足它的一条直角边等于斜边的一半．
在图④中，AE=14a，AB=AD=12a，
故∠ABE=30∘， ∠EAB=60∘，
从而可得∠BAC=∠DAC=60∘，∠ACB=30∘，
故能满足它的一条直角边等于斜边的一半．
综上可得有2个满足条件．
故选C．
二、填空题
【答案】
相等的角是对顶角,假
【考点】
命题与定理
【解析】
把一个命题的条件和结论互换就得到它的逆命题．
【解答】
解：“对顶角相等”的条件是：两个角是对顶角，
结论是：这两个角相等，
所以逆命题是：相等的角是对顶角，它是假命题．
故答案为：相等的角是对顶角；假.
【答案】
5
【考点】
勾股定理
非负数的性质：偶次方
非负数的性质：算术平方根
【解析】
直接利用偶次方的性质以及二次根式的性质得出a，b的值，再利用勾股定理得出斜边长．
【解答】
解：∵ a−3+(b−4)2=0，
∴ a=3，b=4，
∴ 该直角三角形的斜边长为：32+42=5．
故答案为：5．
【答案】
12
【考点】
定义新符号
算术平方根
【解析】
根据新定义的运算法则a※b=a+ba−b，得出12+412−4=168=48=12.
【解答】
解：根据新定义的运算法则a※b=a+ba−b，
可得12※4=12+412−4=168=48=12.
故答案为：12.
【答案】
112.5∘
【考点】
平行四边形的性质
平行线的性质
【解析】
直接利用旋转的性质得出∠BAB′=45∘，AB=AB′，进而结合等腰三角形的性质和平行四边形的性质得出答案．
【解答】
解：∵ ▱ABCD绕点A逆时针旋转45∘，得到▱ AB′C′D′，
∴ ∠BAB′=45∘，AB=AB′，
∴ ∠ABB′=∠AB′B=67.5∘，
∴ ∠C=180∘−67.5∘=112.5∘．
故答案为：112.5∘．
【答案】
2,6，5,6，8,6
【考点】
勾股定理
等腰三角形的性质
【解析】
当PA=PO时，根据P在OA的垂直平分线上，得到P的坐标；当OP=OA=10时，由勾股定理求出CP即可；当AP=AO=10时，同理
求出BP、CP，即可得出P的坐标．
【解答】
解：当PA=PO时，P在OA的垂直平分线上，
P的坐标是5,6，
当OP=OA=10时，由勾股定理得：CP=OP2−OC2=8，
P的坐标是8,6，
当AP=AO=10时，同理BP=8，CP=10−8=2，
P的坐标是2,6，
故答案为：2,6，5,6，8,6.
三、解答题
【答案】
解：(1)原式=48÷3−12×12+26
=4−6+26=4+6 .
(2)原式=24×13−4×24×1=22−2=2.
【考点】
二次根式的混合运算
【解析】
暂无
暂无
【解答】
解：(1)原式=48÷3−12×12+26
=4−6+26=4+6 .
(2)原式=24×13−4×24×1=22−2=2.
【答案】
解：(1)∵ x=3+1 ，y=3−1，
∴ x2+y2−xy=(x+y)2−3xy
=(3+1+3−1)2−3×(3+1)×(3−1)
=232−3×3−1=12−3×2=12−6=6 .
(2)∵ 4