2022年中考数学二轮专题《直角三角形探究》（含答案）

这是一份2022年中考数学二轮专题《直角三角形探究》（含答案），共7页。试卷主要包含了选择题，填空题，解答题，综合题等内容，欢迎下载使用。
一、选择题
在Rt△ABC中，∠A=90°，有一个锐角为60°，BC=6.若P在直线AC上(不与点A，C重合)，且∠ABP=30°，CP的长不可能的是( )
A.2eq \r(3) B.4eq \r(3) C.8 D.6
如图，在△ABC中，∠C=90°，AC＞BC，若以AC为底面圆半径、BC为高的圆锥的侧面积为S1，
以BC为底面圆半径、AC为高的圆锥的侧面积为S2，则( )
A.S1=S2 B.S1＞S2 C.S1＜S2 D.S1、S2的大小关系不确定
如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=2eq \r(2)，CD=eq \r(2)，点P在四边形ABCD上，若P到BD的距离为eq \f(3,2)，则点P的个数为( )
A.1 B.2 C.3 D.4
如图，将△ADE绕正方形ABCD(四条边都相等，四个角都是直角)的顶点A顺时针旋转90°得△ABF，连接EF交AB于点H；
则下列结论：
①AE⊥AF；
②△ABF≌△AED；
③点A在线段EF的中垂线上
④△ADE与△ABF的周长和面积分别相等；
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
在Rt△ACB中，∠C=90°，AC=BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC、BC边分别相交于E、F，连接EF，则在运动过程中，△OEF与△ABC的关系是( )
A.一定相似
B.当E是AC中点时相似
C.不一定相似
D.无法判断
如图，在Rt△ABC中，∠C=90°，AB=5，BC=4．点P是边AC上一动点，过点P作PQ∥AB交BC于点Q，D为线段PQ的中点，当BD平分∠ABC时，AP的长度为( )
如图，△ABC中，∠ACB=90°，AB=10，tanA=.点P是斜边AB上一个动点.过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（ ）
如图,己知△ABC中,∠C=90°,∠A=30°,AC=.动点D在边AC上,以BC为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为（ ）

A. B. C. D.
二、填空题
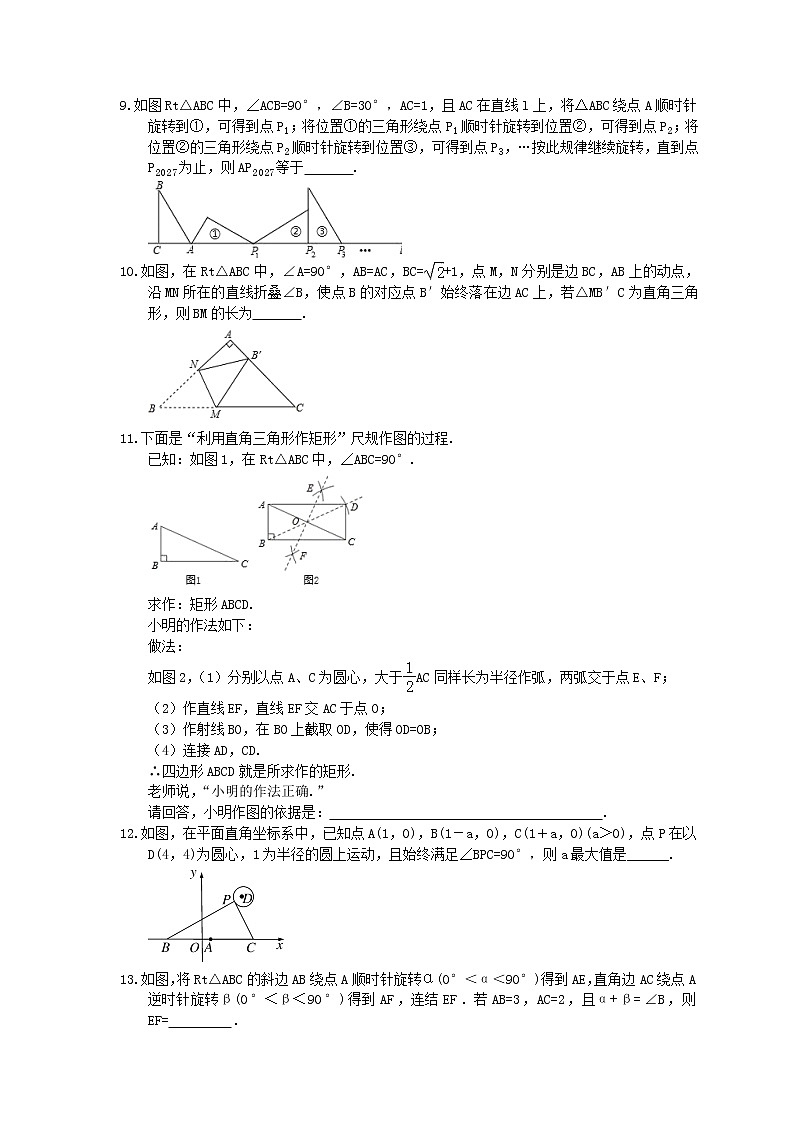
如图Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，且AC在直线l上，将△ABC绕点A顺时针旋转到①，可得到点P1；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，…按此规律继续旋转，直到点P2027为止，则AP2027等于 .
如图，在Rt△ABC中，∠A=90°，AB=AC，BC=+1，点M，N分别是边BC，AB上的动点，沿MN所在的直线折叠∠B，使点B的对应点B′始终落在边AC上，若△MB′C为直角三角形，则BM的长为 .
下面是“利用直角三角形作矩形”尺规作图的过程.
已知：如图1，在Rt△ABC中，∠ABC=90°.
求作：矩形ABCD.
小明的作法如下：
做法：
如图2，（1）分别以点A、C为圆心，大于AC同样长为半径作弧，两弧交于点E、F；
（2）作直线EF，直线EF交AC于点O；
（3）作射线BO，在BO上截取OD，使得OD=OB；
（4）连接AD，CD.
∴四边形ABCD就是所求作的矩形.
老师说，“小明的作法正确.”
请回答，小明作图的依据是： .
如图，在平面直角坐标系中，已知点A(1，0)，B(1－a，0)，C(1＋a，0)(a＞0)，点P在以D(4，4)为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a最大值是______.
如图，将Rt△ABC的斜边AB绕点A顺时针旋转α(0°＜α＜90°)得到AE，直角边AC绕点A逆时针旋转β(0°＜β＜90°)得到AF，连结EF．若AB=3，AC=2，且α+β=∠B，则EF= ．
三、解答题
如图，在平面直角坐标系中，点C(0，4)，射线CE∥x轴，直线y=－eq \f(1,2)x＋b交线段OC于点B，交x轴于点A，D是射线CE上一点.若存在点D，使得△ABD恰为等腰直角三角形，求b的值.
(1)如图1，在△ABC中，点M为BC边的中点，且MA=BC，求证：∠BAC=90°.
(2)如图2，直线a、b相交于点A，点C、E分别是直线b、a上两点，ED⊥b，垂足为点D，点M是EC的中点，MD=MB，DE=2，BC=3，求△ADE和△ABC的面积之比.
四、综合题
在平面直角坐标系中，抛物线y=x2＋(k－1)x－k与直线y=kx＋1交于A，B两点，点A在点B的左侧.
(1)如图1，当k=1时，求A，B两点的坐标；
(2)如图2，抛物线y=x2＋(k－1)x－k(k＞0)与x轴交于点C，D两点(点C在点D的左侧)，在直线y=kx＋1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由.
答案解析
1.答案为：C.
解析：①当∠C=60°时，∠ABC=30°，如图①，与∠ABP=30°矛盾；
②当∠C=60°，如图②，∵∠ABP=30°，∴∠CBP=60°，∴CP=BC=6；
③当∠ABC=60°时，∠C=30°，如图③，∵∠ABP=30°，∴∠C=∠ABP=30°，
∴PC=PB，∵BC=6，∴AB=3，∴PC=PB=2eq \r(3)；
④当∠ABC=60°时，∠C=30°，如图④，∵∠ABP=30°，∴∠PBC=90°，
∴PC=4eq \r(3).故不能为8，选C.
2.答案为：B.
3.答案为：B.
4.答案为：A.
5.答案为：A.
6.答案为：B.
7.答案为：B.
8.答案为：A
9.答案为：2027+676eq \r(3).
10.答案为： +或1.
11.答案为：到线段两段点的距离相等的点在这条线段的垂直平分线上；
对角线互相平分的四边形为平行四边形；
有一个内角为90°的平行四边形为矩形.
12.答案为：6；
解析：∵A（1，0），B（1－a，0），C（1＋a，0）（a＞0），
∴AB=1－（1－a）=a，CA=a＋1－1=a，∴AB=AC.
∵∠BPC=90°，∴PA=AB=AC=a.
如图，延长AD交⊙D于P′，此时AP′最大.
∵A（1，0），D（4，4），
∴AD=5，∴AP′=5＋1=6，∴a的最大值为6.
13.答案为：
14.解：分三种情况讨论：
①当∠ABD=90°时，如图1，b=eq \f(4,3)；
②当∠ADB=90°时，如图2，b=eq \f(8,3)；
③当∠DAB=90°时，如图3，b=2
15. (1)证明：∵点M为BC的中点，
∴BM=CM=BC.
∵MA=BC，
∴BM=CM=MA，
∴∠BAM=∠B，∠CAM=∠C，
∴∠BAM+∠B+∠CAM+∠C=180°，
∴2∠BAM+2∠CAM=180°，
∴∠BAM+∠CAM=90°，即∠BAC=90°.
(2)解：∵点M为EC的中点，ED⊥AC于点D，
∴DM=EC.
∵BM=DM，
∴BM=EC，
∴∠EBC=90°.
∴∠ADE=∠ABC=90°.
又∵∠DAE=∠BAC，
∴△ADE∽△ABC，
∴=()2=.
四、综合题
16.解：(1)A(－1，0)，B(2，3)
(2)设直线AB：y=kx＋1与x轴，y轴分别交于点E，F，
则E(－eq \f(1,k)，0)，F(0，1)，OE=eq \f(1,k)，OF=1.
在Rt△EOF中，由勾股定理得：
EF=eq \r(（\f(1,k)）2＋1)=eq \f(\r(1＋k2),k).
令y=x2＋(k－1)x－k=0，得：x=－k或x=1.
∴C(－k，0)，OC=k.
①假设存在唯一一点Q，使得∠OQC=90°，
如图，则以OC为直径的圆与直线AB相切于点Q，此时∠OQC=90°.
设点N为OC中点，连结NQ，则NQ⊥EF，NQ=CN=ON=eq \f(k,2).∴EN=OE－ON=eq \f(1,k)－eq \f(k,2).
∵∠NEQ=∠FEO，∠EQN=∠EOF=90°，∴△EQN∽△EOF，∴eq \f(NQ,OF)=eq \f(EN,EF)，
即：eq \f(\f(k,2),1)=eq \f(\f(1,k)－\f(k,2),\f(\r(1＋k2),k))，解得：k=±eq \f(2\r(5),5)，∵k>0，∴k=eq \f(2\r(5),5).
∴存在唯一一点Q，使得∠OQC=90°，此时k=eq \f(2\r(5),5).
②若直线AB过点C时，此时直线与圆的交点只有另一点Q点，故亦存在唯一一点Q，
使得∠OQC=90°，将C(－k，0)代入y=kx＋1中，可得k=1，k=－1(舍去)，
故亦存在唯一一点Q，使得∠OQC=90°，此时k=1.
综上所述，k=eq \f(2\r(5),5)或1时，存在唯一一点Q，使得∠OQC=90°