高中湘教版（2019）3.4 复数的三角表示教案设计

这是一份高中湘教版（2019）3.4 复数的三角表示教案设计，共14页。教案主要包含了教学目标，教学重点，教学难点，教学方法，教学手段，核心素养，教学过程等内容，欢迎下载使用。
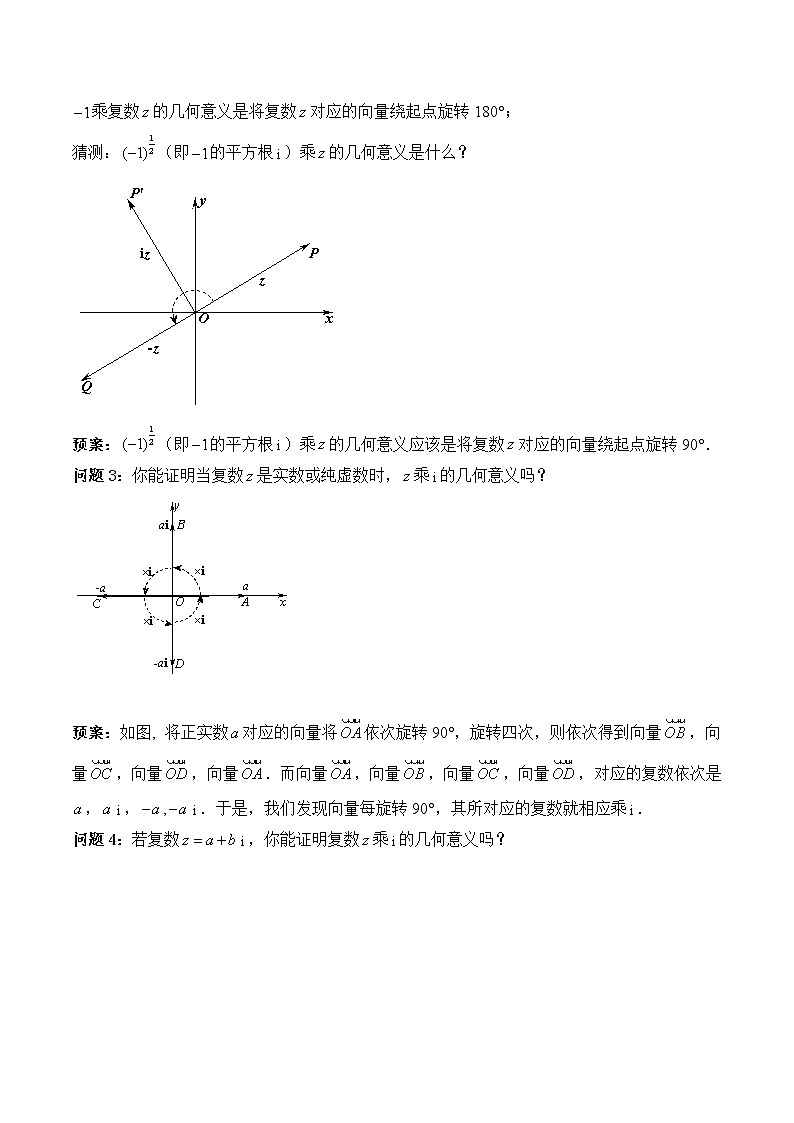
复数的三角表示【教学目标】1．了解的几何意义，了解的几何意义就是将复数对应的平面向量旋转90°；了解复数的三角表示，能够把复数的代数形式化为三角形式；了解复数的三角形式的乘法运算和除法运算，了解复数的三角形式的乘法运算和除法运算的几何意义．2．通过对的几何意义的探究，培养学生观察、归纳、抽象的能力和语言表达能力；通过复数的三角表示、复数乘法和除法运算的三角表示及其几何意义的探究，培养学生发现问题、提出问题、分析问题和解决问题的能力、提高学生的推理论证能力． 3．通过知识的探究过程培养学生细心观察、认真分析、严谨论证的良好思维习惯，让学生经历从具体到抽象，从特殊到一般，从感性到理性的认知过程．【教学重点】  复数的三角表示；复数的三角形式的乘法运算和除法运算．【教学难点】  的几何意义；复数的三角形式的乘法运算和除法运算的几何意义．【教学方法】  教师启发讲授，学生探究学习．【教学手段】  计算机、投影仪．【核心素养】  数学抽象，逻辑推理，数学运算．【教学过程】第1课时一、创设情境，引入课题课前布置任务：如图，设平面向量，对应复数，则，对应复数.由于，因此可由绕起点逆时针旋转180°得到．由可知，从旋转的角度，你认为乘复数的几何意义是什么？预案：由可知，乘复数的几何意义是将复数对应的向量绕起点逆时针旋转180°变成．〖设计意图〗通过问题的引入，激发学生学习的兴趣，为的几何意义做铺垫．二、实例探索，归纳规律1．的几何意义问题1：由可知，乘复数的几何意义是将复数对应的向量绕起点旋转180°变成．将连乘两个得到就是将向量连续旋转两个180°，也就是旋转360°，仍得到. 乘复数的几何意义是什么？预案：乘复数的几何意义是将复数z对应的向量旋转两个180°，也就是360°．问题2：乘复数的几何意义是将复数z对应的向量旋转360°；乘复数的几何意义是将复数对应的向量绕起点旋转180°；猜测：（即的平方根）乘的几何意义是什么？预案：（即的平方根）乘的几何意义应该是将复数对应的向量绕起点旋转90°．问题3：你能证明当复数是实数或纯虚数时，乘的几何意义吗？ 预案：如图, 将正实数对应的向量将依次旋转90°，旋转四次，则依次得到向量，向量，向量，向量．而向量，向量，向量，向量，对应的复数依次是，，,．于是，我们发现向量每旋转90°，其所对应的复数就相应乘． 问题4：若复数，你能证明复数乘的几何意义吗？预案：复平面上的点P表示复数，设向量，分别表示，， 由知向量，是矩形OAPB的对角线．将矩形OAPB绕原点O旋转90°，则向量，向量分别变成向量，向量，矩形OAPB变成矩形．向量，向量所对应的复数应分别由向量，向量所对应的复数乘得到，即向量对应的复数为， 对应的复数为．因此，矩形的对角线表示的向量，所对应的复数为向量旋转90°得到向量，对应的复数为 ，也就是说向量的对应的复数由向量对应的复数乘得到．由此可得，虚数单位乘任意复数的几何意义是：将复数对应的平面向量旋转90°．问题5：你能从旋转的角度得到的几何意义吗？预案：从旋转的角度我们可以得到的几何意义是：将复数对应的平面向量依次旋转两次90°得到的平面向量对应的复数是．也可以这么理解为：将复数对应的平面向量旋转90°得到的平面向量对应的复数是．〖设计意图〗让学生经历归纳—猜想——证明的数学问题的发现过程，培养学生合作、交流和表达能力，培养学生抽象概括和逻辑推理的数学素养．2．旋转任意角问题6：把复数对应的向量旋转90°得到的向量对应的复数是，把复数对应的向量旋转180°得到的向量对应的复数是，那么把复数对应的向量旋转任意角得到的向量对应的复数是什么呢？预案：如图把复数对应的向量旋转角得到，把旋转90°得到，,方向上的单位向量分别为，，由平面向量基本定理可知，，设，，，，由三角函数的定义可知，，，即，，所以．所以 对应的复数为可看作是由乘得到．所以复数对应的向量旋转任意角得到的向量对应的复数是．问题7：乘的几何意义是什么？预案：乘的几何意义是将复数对应的平面向量旋转角．〖设计意图〗让学生经历提出问题——分析问题——解决问题过程，体验研究数学问题的方法，培养学生合作、交流和表达能力，培养学生抽象概括和逻辑推理的数学素养．三、学以致用，深化规律例题1：将平面直角坐标系中任意点绕原点旋转90°得到，求的坐标．预案：因为点对应的复数为，所以将点绕原点旋转90°得到对应的复数为，因此点的坐标．〖设计意图〗通过实例，让学生体验虚数单位乘任意复数的几何意义的应用．培养学生合作、交流和表达能力，培养学生逻辑推理的数学素养．例题2：根据乘的几何意义计算：（1）；（2）．预案：（1），因为用乘任意复数，其几何意义是将对应的向量旋转45°，所以用 乘的几何意义是将对应的向量连续旋转两个45°，也就是将对应的向量旋转90°，又由虚数单位乘任意复数的几何意义可知，，即．（2），因为用乘任意复数，其几何意义是将对应的向量旋转120°，所以用 乘的几何意义是将对应的向量连续旋转三个120°，也就是将对应的向量旋转360°，因而，即．〖设计意图〗通过实例，让学生体验乘任意复数的几何意义的应用．培养学生合作、交流和表达能力，培养学生逻辑推理的数学素养．练习：将复数对应的向量旋转，求所得向量对应的复数． 预案：（1），四、归纳小结，提高认识学生交流在本节课学习中的体会、收获，交流学习过程中的体验和感受，师生合作共同完成小结．1．小结(1) 知识探究过程：归纳—猜想—证明．(2) 方法：乘的几何意义是将复数对应的平面向量旋转角．(3) 数学思想方法和思维方法：等价转化．2．作业课后探究：根据乘的几何意义计算：（1）；（2）．第2课时一、创设情境，引入课题课前布置任务：    我们已经知道用复数乘复数，就是把复数对应的平面向量旋转任意角.怎样的复数能够写成的形式呢?〖设计意图〗通过问题的引入，激发学生学习的兴趣，为引入复数的三角形式做铺垫．二、实例探索，归纳规律1．复数的三角表示问题1：如图，复数在复平面内用向量表示. 我们把以x轴的正半轴为始边，以为终边的角，称为复数的辐角，记作.若是的一个辐角，则的全部辐角可以如何表示？预案：若是的一个辐角，全部辐角可以表示为.问题2：复数，设，根据三角函数的定义，，如何表示？你能把复数用，表示吗？预案：复数，设，根据三角函数的定义，，，即，，因而． 问题3：我们把叫做复数的三角形式．其中为复数的模，为复数的一个辐角．叫做复数的代数形式．当时，能表示为形式吗？预案：特别地当时，显然，此时辐角可以取任意值，因此复数也可以有形式．〖设计意图〗让学生经历归纳—猜想——证明的数学问题的发现过程，培养学生合作、交流和表达能力，培养学生抽象概括和逻辑推理的数学素养．2．复数的三角形式的运算问题4：设复数，复数，从旋转的角度你能得到的几何意义吗？预案：画出,对应的向量，，乘 可分两步实现：首先,用乘,得到,对应的向量 由对应的向量 旋转角得到,此时模，辐角．然后,用乘得到，对应的向量由对应的向量乘实数而伸缩得到，此时模，辐角．由此得复数与的乘法公式：．上式表明，两个复数乘积的模等于它们的模的乘积，乘积的辐角等于它们的辐角之和．问题5：设复数，复数，利用复数的乘法法则你能得到的乘法公式吗？预案：根据两角和的正弦和余弦公式，有．问题6：我们知道，除法是乘法的逆运算，设复数，复数，你能根据复数的三角形式乘法公式得到复数除法公式吗？预案：设，所以，又因为，，根据复数相等的条件，有，因此，．复数，的除法公式：．问题7：复数，，你能根据复数的除法法则得到复数三角形式的除法公式吗？预案：根据两角差的正弦和余弦公式，有．上式表明，两个复数相除（除数不为0），商的模等于它们的模的商，商的辐角等于它们的辐角之差．问题8：复数，，，…，其中，利用复数的三角形式的乘法法则你能得到的乘法公式吗？预案：．问题9：复数，利用复数的三角形式的乘法法则你能得到()的公式吗？ 预案：．〖设计意图〗让学生经历提出问题——分析问题——解决问题过程，体验研究数学问题的方法，培养学生合作、交流和表达能力，培养学生抽象概括和逻辑推理的数学素养．三、学以致用，深化规律例题1：把复数化为三角形式．预案：如图，复数对应的点在第二象限，因而，，所以辐角，，由于复数的辐角不是唯一的，因而复数的的三角形式也不是唯一的，所以当时，复数的三角形式为．所以当时，复数的三角形式为．所以当时，复数的三角形式为．……你能总结把复数的代数形式化为三角形式的步骤吗？预案：①确定对应的点所在的象限；②计算；③由和点所在象限确定辐角的值（不唯一，它们之间相差的整数倍）；④写出复数的三角形式．例题2：计算：．预案：因为，所以．〖设计意图〗通过实例，让学生体验复数的三角形式的乘法公式的应用．培养学生合作、交流和表达能力，培养学生逻辑推理和数学运算的数学素养．例题3：计算：．预案： ．〖设计意图〗通过实例，让学生体验复数的三角形式的除法公式的应用．培养学生合作、交流和表达能力，培养学生逻辑推理和数学运算的数学素养．例题4：解方程，并将其所有的根用复平面上的点表示，观察以这些点为顶点的多边形是什么形状．预案1：方程可化为，方程左边分解因式：，所以原方程可化为，即或，当时，；当时，，．所以方程的三个根为，，．在复平面上画出表示这三个根的点,,,如图所示．观察发现，以这三点为顶点的△是以原点为圆心的单位圆的内接正三角形，三个顶点等分圆周． 预案2：设， ，因为相等的复数的模相等，其辐角可以相差2的整数倍．所以,即当时，；当时，；当时，；当时，；由于正弦、余弦函数的周期都是2π，所以当取时，又会重复出現取时的结果．所以方程的三个根为，，．在复平面上画出表示这三个根的点,,,如图所示．观察发现，以这三点为顶点的△是以原点为圆心的单位圆的内接正三角形，三个顶点等分圆周．〖设计意图〗通过实例，让学生体验求复数的三次方根的过程．培养学生分析问题和解决问题的能力，培养学生合作、交流和表达能力，培养学生逻辑推理和数学运算的数学素养．练习：1.把化为三角形式．预案如图，复数对应的点在第四象限，因而 ，，辐角，，由于复数的辐角不是唯一的，因而复数的的三角形式也不是唯一的，所以当时，复数的三角形式为．所以当时，复数的三角形式为．所以当时，复数的三角形式为． ……2. 计算：．预案： ．3. 计算：．预案： ．4. 计算：．预案：因为，所以．四、归纳小结，提高认识学生交流在本节课学习中的体会、收获，交流学习过程中的体验和感受，师生合作共同完成小结．1．小结(1) 知识探究过程：归纳—猜想—证明．(2) 方法：把复数的代数形式化为三角形式的方法；复数的三角形式的乘法公式和除法公式．(3) 数学思想方法和思维方法：等价转化．2．作业课后探究：设是复数的n ()次方根，探究与，与的关系．