2021学年9.4 乘法公式教案

 课题： 9.4  乘法公式（1）

执 笔

二 次 备 课

时 间

学习目标

1．会推导完全平方公式，并能运用公式进行简单的计算；

2．通过图形面积的计算，感受乘法公式的直观解释；

3．经历探索完全平方公式的过程，发展学生的符号感和推理能力．

学习重点

运用完全平方公式进行简单的计算．

学习难点

完全平方公式的应用．

学时安排

1课时

学法指导

合作探究，自主练习

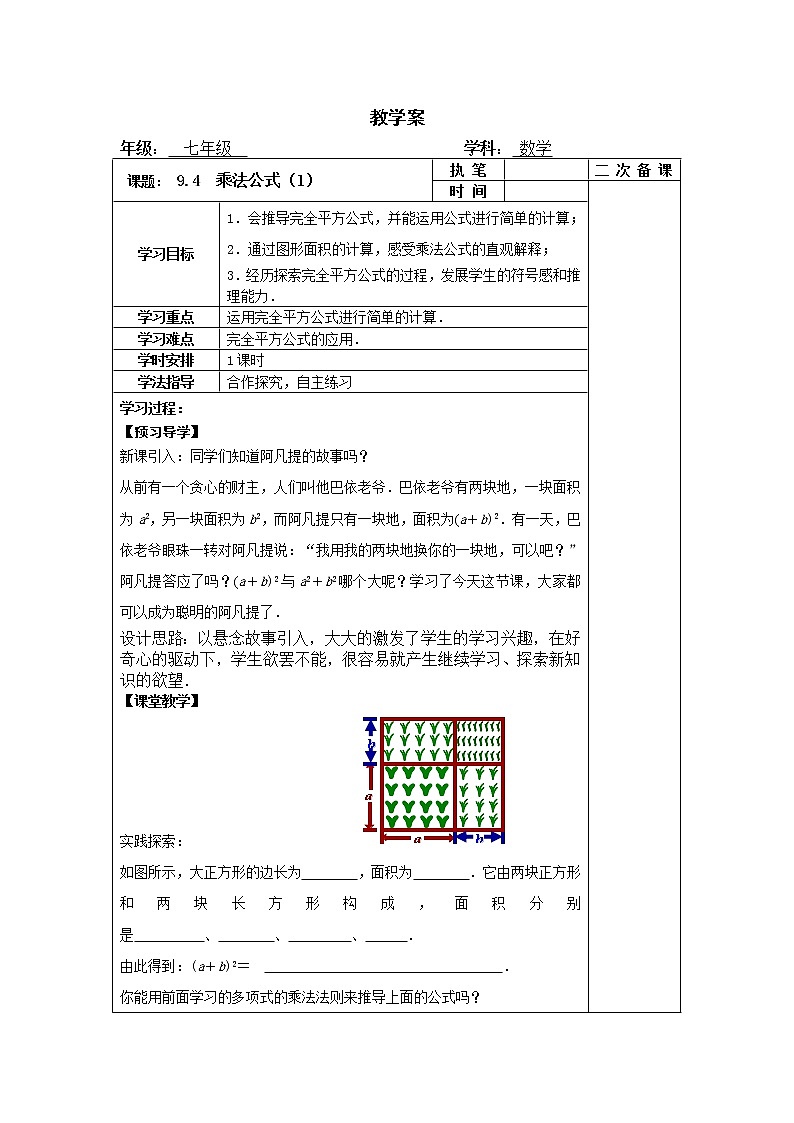
学习过程：

【预习导学】

新课引入：同学们知道阿凡提的故事吗？

从前有一个贪心的财主，人们叫他巴依老爷．巴依老爷有两块地，一块面积为a2，另一块面积为b2，而阿凡提只有一块地，面积为(a＋b)2．有一天，巴依老爷眼珠一转对阿凡提说：“我用我的两块地换你的一块地，可以吧？”

阿凡提答应了吗？(a＋b)2与a2＋b2哪个大呢？学习了今天这节课，大家都可以成为聪明的阿凡提了．

设计思路：以悬念故事引入，大大的激发了学生的学习兴趣，在好奇心的驱动下，学生欲罢不能，很容易就产生继续学习、探索新知识的欲望．

【课堂教学】

实践探索：

如图所示，大正方形的边长为        ，面积为        ．它由两块正方形和两块长方形构成，面积分别是          、        、         、      ．

由此得到：(a＋b)2＝                                   ．

你能用前面学习的多项式的乘法法则来推导上面的公式吗？

(a＋b)2＝                                            ．

这个公式称为完全平方公式 （出示课题） ．

设计思路：学生自主观察、思考、回答问题．一生上黑板板书用多项式的乘法法则推导(a＋b)2的结果。

【小组讨论】

设计思路：让学生自主解决问题，发现问题解决的方法多样，板书展示，教师点评表扬，鼓励学生积极思考，主动解决问题。

一生：直接利用多项式的乘法法则推导(a－b)2的结果。

一生：利用(a－b)2=[a+(－b)]2推导。

设计思路：尝试多种方法解题并找出最优化方法，可以提高学生解题的策略性．把两数差转化为两数和，引导学生感受转化的思想以及知识之间的内在联系．

由例1，得出(a－b)2＝a2－2ab＋b2．这个公式也称为完全平方公式．

(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2．

你能说出这两个公式的特点吗？根据公式特点，教师引导学生完善完全平方公式口诀：首平方，尾平方，首尾两倍放中间，符号看前方．

举一反三：计算（1）(－a＋b)2  ）     （2）(－a－b)2

学以致用：例2、 用完全平方公式计算：

（1）(5＋3p)2；（2）(2x－7y)2； （3）(－2a－5)2．

设计思路：学生板书，教师点评，规范格式，巩固公式．

例3 、计算：（1）9982；      （2）20012．

设计思路：通过灵活运用公式可以简化运算，培养学生的综合能力．

【总结提升】

1、完全平方公式：(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2．

2、在解题过程中要正确确定a和b、对照公式原形的两边，做到不丢项、不弄错符号、2ab时不能少乘2.

3、完全平方公式的灵活运用，应掌握公式的简单变形.

【当堂检测】

1．用完全平方公式计算：（1）(1＋x)2；（2）(y－4)2；（3）(－3x＋2)2．  

2．请你来诊断： （1）(x＋y)2＝x2＋y2； （2）(x－y)2＝x2－y2；

（3）(－m＋n)2＝－m2＋n2； （4）(－a－1)2＝a2－2a－1．

3．用简便方法计算992．

4．如图所示，内外两个均为正方形，则小正方形的边长为多少

cm？大正方形的面积比小正方形大多少？  3 

【布置作业】

补充习题

教学反思

                                           授课人：（签名）

                                                        年    月    日