2022年中考数学专题复习：平行四边形的计算与证明课件

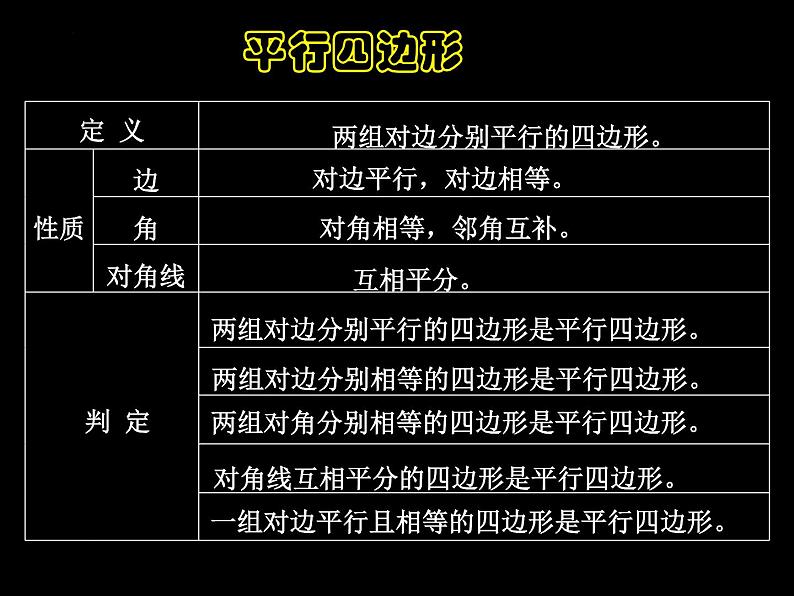
这是一份2022年中考数学专题复习：平行四边形的计算与证明课件，共41页。PPT课件主要包含了知识梳理，平行四边形，对边平行对边相等，对角相等邻角互补，互相平分，几何中的距离，两点之间线段最短，垂线段最短，三角形的中位线，位置关系等内容，欢迎下载使用。
两组对边分别平行的四边形。
两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
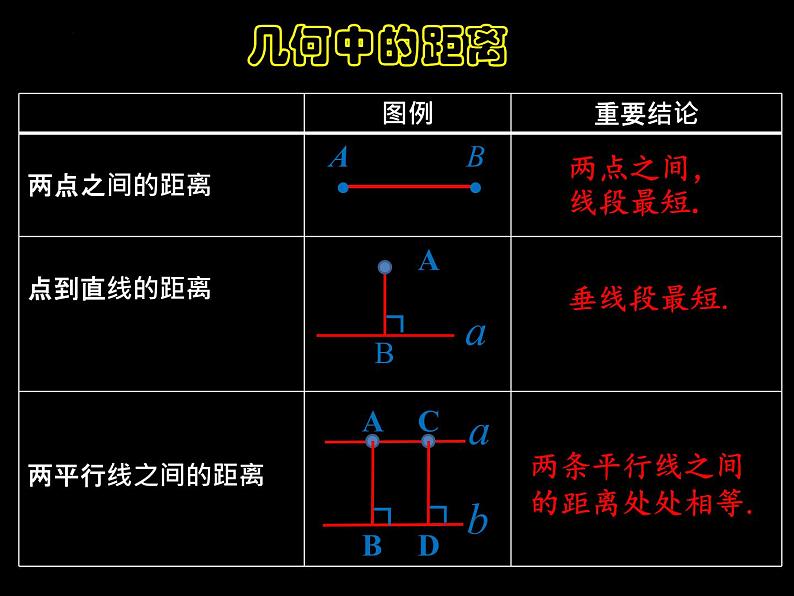
两条平行线之间的距离处处相等.
三角形的中位线平行于三角形的第三边，
连接三角形两边中点的线段叫做三角形的中位线。
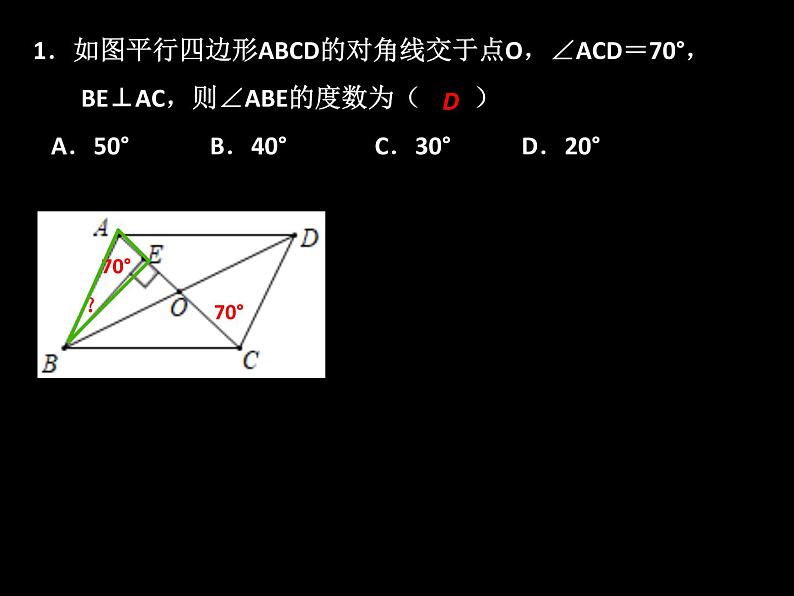
1．如图平行四边形ABCD的对角线交于点O，∠ACD＝70°， BE⊥AC，则∠ABE的度数为（　　） A．50° B．40° C．30° D．20°
2. 如图，□ ABCD的周长为60cm，对角线AC、BD相交于点O， △AOB的周长比△BOC的周长多8cm，则AB＝____cm.
AB+BC＝30AB -BC＝8
3.如图，在平行四边形ABCD中，E为边CD上一点，将△ADE沿 AE折叠至△AD′E处，AD′与CE交于点F，若∠B＝52°， ∠DAE＝20°，则∠FED′的大小为________．
4．如图，已知平行四边形ABCD，CD＝3cm，依下列步骤作图，并 保留作图痕迹：步骤1：以B为圆心，BE长为半径画弧①，分别交AB，BC于点E，F；步骤2：以A为圆心，以BE长为半径画弧②，交AD于点G；步骤3：以G为圆心，以EF长为半径画弧③，弧②和弧③交于点H， 过H作射线，交BC于点M．则下列叙述不正确的是（　　）A．∠AMC＝∠C B．AM＝CDC．AM平分∠BAD D．△BEF≌△AGH
如图，已知平行四边形ABCD中，∠BCD的平分线CE交边 AD于E，∠ABC的平分线BG交CE于F，交AD于G． 求证：AE=DG．
∵四边形ABCD是平行四边形，
∴BC ∥ AD，AB=DC，
∴ ∠AGB=∠GBC， ∠DEC=∠BCE，
又∵ BG平分∠ABC， CE平分∠BCD，
∴ ∠ABG=∠GBC， ∠DCE=∠BCE，
∴ ∠ABG=∠AGB， ∠DCE=∠DEC，
∴ AB=AG， DE=DC，
∴ AG － EG= DE － EG，
6．如图，E是平行四边形ABCD的边CD的中点，延长AE交BC 的延长线于点F．（1）求证：AE＝EF；
∵ E是边CD的中点，
∴ △AED≌△FEC（AAS），
又∵ ∠AED=∠FEC，
（2）若∠BAF＝90°，BC＝15，EF＝9，求CD的长．
∵∠BAF＝90°，
∴ AF=AE+EF=9+9=18.
∴BC = AD，AB=CD.
∵ △AED≌△FEC（AAS），
∴ BF=BC+CF=15+15=30.
1．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断 四边形ABCD是平行四边形的是（　）A．∠ABD＝∠BDC，OA＝OC B．∠ABC＝∠ADC，AB＝CDC．∠ABC＝∠ADC，AD∥BC D．∠ABD＝∠BDC，∠BAD＝∠DCB
2.如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、 等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为F，连结DF．（1）试说明AC＝EF；
∵△ABE为等边三角形，
∴AB=AE=EB，∠BAE=60°，
又∵ EF⊥AB，垂足为F，
∴ ∠ABC＝60°，
Rt△ABC中， ∵ ∠BAC＝30°，AB为斜边
∵ ∠ABC＝∠EAF，∠ACB＝∠AFE，AC=EF，
∴ ∠AFE＝90°，
∴ △ABC≌△EAF（AAS）
（2）求证：四边形ADFE是平行四边形．
∵△ACD为等边三角形，
∴AC=AD，∠DAC=60°，
∵ AC=EF， ∠BAC＝30°，
∴EF=AD，∠DAB =∠DAC ＋ ∠BAC=60° ＋ 30° =90°，
∵ ∠DAB =∠EFA=90°，
∴四边形ADFE是平行四边形．
如图，已知直线a∥b，点A、B在直线a上，点C、D在直线b上，线段BC、AD相交于点E，写出图中面积相等的三角形：___________.
1．如图，在平行四边形ABCD中，对角线AC，BD相交于点O， 点E，F分别是AD，OD的中点，若EF＝2，则AC的长是（ ） A．2B．4 C．6D．8
2．如图，在平行四边形ABCD中，对角线AC与BD相交于点O， AC⊥CD，E为CD中点，连接OE. 若OC＝4，CE＝3，则BC的 长是　 　．
3. 如图，点E、F、G、H分别是线段AB、BC、CD、AD的中点，则四边形EFGH是什么图形？并说明理由。
∵点E、F、G、H分别是线段AB、 BC、CD、 AD的中点，
∴EF、GH分别是△BAC、△DAC的中位线，
∴EF ∥ HG，且 EF=HG ，
∴四边形EFGH为平行四边形.
四边形EFGH为平行四边形.
平行四边形的性质与判定的综合
1．如图，点B、F、C、E在一条直线上，FB＝CE，AB∥ED， AC∥FD，AD交BE于点O．（1）求证：AD与BE互相平分；
∴ BF+FC=CE+FC，
∵ AB∥ED，AC∥FD，
∴ ∠B=∠E， ∠ACB=∠DFE，
∴ △ABC≌△DEF（ASA）.
∴四边形ABDE是平行四边形，
∴AD与BE互相平分.
∵ AB∥ DE，且AB=DE，
（2）若AB⊥AC，AC＝BF，BE＝8，FC＝2，求AB的长．
∴ BF=CE=（8-2） ÷ 2=3，
BF+FC+CE=BE=8，
∴ BC=BF+FC=3+2=5，AC＝BF=3，
∴ ∠BAC＝90°，
2．如图，平行四边形ABCD中，点E、F分别在边BC、AD上， EA⊥AC，FC⊥AC．（1）求证：△ABE≌△CDF；
∴AB ∥ CD，AB=CD， ∠B= ∠D.
∵ EA⊥AC，FC⊥AC．
∴ ∠EAC= ∠FCA=90° .
∴ ∠BAC= ∠DCA .
∴ ∠BAC－ ∠EAC = ∠DCA－ ∠FCA，
即 ∠BAE= ∠DCF.
∴ △ABE≌△CDF（ASA）
∴AD∥ BC，AB=CD， AD=BC， ∠B= ∠D.
∵点E、F分别在边BC、AD上，
∵AE∥ CF， AF∥ EC，
∴四边形AECF是平行四边形，
∴ AD－AF=BC－CE，
∴ △ABE≌△CDF（SAS）
（2）若∠B＝30°，∠AEC＝45°，求证：AB＝AF．
过点A作AG⊥EC于点G，
（直角三角形斜边上的中线等于斜边的一半.）
∵EA⊥AC，∠AEC＝45°，
∴ ∠ACE=180°－ ∠EAC － ∠AEC = 180°－90°－45°=45°，
∵∠AEC＝ ∠ACE，
∵AE=AC，AG⊥EC，
∵AG⊥EC， ∠B＝30°，
∵△ABE≌△CDF，
∴ AD－DF=BC－BE，
平行四边形中的动点问题
1．如图，四边形ABCD中，AD∥BC，AD＝3，BC＝8，E是BC的中点，点P以每秒 1个单位长度的速度从A点出发，沿AD向点 D运动；点Q同时以每秒2个单位 长度的速度从点C出发，沿 CB向点B 运动，点P停止运动时，点Q也随之停止 运动．当运动时间t＝　 　 秒时，以点 P，Q，E，D为顶点的四边形 是平行四边形．
2．如图，四边形ABCD中，∠A＝∠ABC＝90°，AD＝1，BC＝3，E是边CD的 中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；
∵ ∠A＝∠ABC＝90°，
∴ ∠A+∠ABC＝180°，
∴ ∠CBE=∠DFE，
∴ △BEC≌△FED（AAS），
又∵ ∠CEB=∠DEF，
∵ BC ∥ DF，且BC=DF，
∴四边形BDFC是平行四边形.
（2）若△BCD是等腰三角形，求四边形BDFC的面积．
∵四边形BDFC是平行四边形，
∵ ∠A= ∠ABC= ∠AGC=90° ，
过点C作CG⊥AF于点G，
∴四边形AGCB是矩形，
∴ DG＝AG﹣AD＝3﹣1＝2，
过点D作DG⊥BC于点G，
显然，前后矛盾，故此时不成立；
∵ ∠A= ∠ABC= ∠DGB=90° ，
∴四边形ABGD是矩形，
∴ CG＝BC﹣BG＝3﹣1＝2，
又∵ DB＝DC， DG⊥BC于点G，
四边形BDFC的面积为
3．如图，平行四边形ABCD中，E为BC边上的一个动点（不与B、 C重合），过点E作直线AB的垂线，垂足为F，FE与DC的延长 线相交于点G．（1）若E为BC中点，求证：BF＝CG；
又∵∠BEF＝ ∠CEG，
∴ △BEF≌△CEG（ASA）
（2）若AB＝5，BC＝10，∠B＝60°，当点E在线段BC上运动时， FG的长度 是否改变？若不变， 求FG；若改变，请说明理由；
过点A作AG⊥BC于点G，
∵AG⊥BC，∠B＝60°，
∴ ∠BAG=180°－ ∠AGB － ∠B = 180°－90°－60°=30°，
∵ AG⊥BC，FG ⊥AB，
（3）在（2）的条件下，H为直线AD上的一点，设BE＝x，若A、B、 E、H四点 构成一个平行四边形，请用含x的代数式表示BH．
在R t △ BHM中，
①当点H在线段AD上时，
过点H作HM⊥BC于M．
又∵ AG⊥BC，HM⊥BC，
∵四边形ABEH是平行四边形，
∴ R t△ABG≌R t △ HEM（HL）
②当点H在线段AD的反向延长线上时，
过点H作HM⊥BC交BC的反向延长线于M．
∵四边形AEBH是平行四边形，
∴ R t△AEG≌R t △ HBM（HL）